Table of Contents
러더퍼드 산란
러더퍼드 산란 실험의 기본 구조는 다음과 같다. 헬륨의 원자핵인 $\alpha$입자를 원자살 형태로 상대적으로 원자번호가 큰 금속으로 만든 얇은 박막에 쏘아준다.
톰슨의 원자 모형
러더퍼드의 산란 실험 이전의 원자 모형으로는 톰슨의 원자 모형이 가장 널리 받아들여지는 모형이었다. 톰슨은 원자가 중성일 것이라 생각하였다. 원자 내부에 양전하들이 고르게 분포되어 있고 그 사이에 음전하가 건포도처럼 박혀 있을 것이라 생각하였다. 이렇게 전하들이 분포되어 있으면 원자가 전기적으로 중성일 것이라 생각할 수 있다. 톰슨의 원자 모형에 따르면 위의 러더퍼드 산란 실험에서 $\alpha$ 입자가 금속 박막을 통과한 뒤의 경로는 처음 들어가는 경로에서 크게 벗어나지 않을 것이라 예측할 수 있다.
간단한 계산
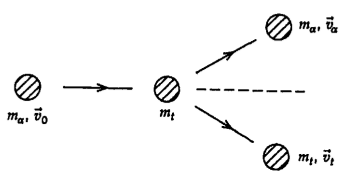
$\alpha$입자가 질량 $m_{\alpha}$을 가지고 초기 속도 $\vec{v}_{0}$로 질량 $m_{t}$인 목표 입자와 충돌하는 상황을 생각하자. 그리고 여기서 $\alpha$입자의 속력은 $v_{0}\ll0.1c$로 빛의 속력보다 매우 작아 상대론적 효과를 무시하자.
운동량 보존과 에너지 보존으로 $\boldsymbol{v_0}$와 $v_0^2$를 계산할 수 있다.
$$m_\alpha\boldsymbol{v_0} = m_\alpha\boldsymbol{v_\alpha} + m_t\boldsymbol{v_t} ~\rightarrow~ \boldsymbol{v_0} = \boldsymbol{v_\alpha} + \frac{m_t}{m_\alpha}\boldsymbol{v_t}$$
$$\frac{1}{2}m_\alpha v_0^2 = \frac{1}{2}m_\alpha v_\alpha^2 + \frac{1}{2}m_tv_t^2 ~\rightarrow~ v_0^2 = v_\alpha^2 + \frac{m_t}{m_\alpha}v_t^2$$
계산에서 $(\boldsymbol{v_i})^2 = \boldsymbol{v_i}\cdot\boldsymbol{v_i}=v_i^2$이고 $i=0,~\alpha$, 그리고 $t$이다. 첫 번째 결과를 두 번째 결과에 대입하면
\begin{equation}\notag
\begin{split}
v_0^2 &= \left(v_\alpha^2 + \left(\frac{m_t}{m_\alpha}\right)^2v_t^2 + 2\frac{m_t}{m_\alpha}\boldsymbol{v_\alpha}\cdot\boldsymbol{v_t}\right)\notag \\
&= v_\alpha^2 + \frac{m_t}{m_\alpha}v_t^2 \notag
\end{split}
\end{equation}
을 얻게 되고
$$v_t^2\left(1-\frac{m_t}{m_\alpha}\right) = \boldsymbol{v_\alpha}\cdot\boldsymbol{v_t}$$
임을 알 수 있다. $m_t\ll m_\alpha$인 경우 좌변이 양수이므로 우변으로부터 $\alpha$입자와 표적입자가 입사방향으로 운동한다는 것을 알수 있고, $m_t\gg m_\alpha$이면 좌변이 음수이므로 과녁 입자가 입사 방향, $\alpha$ 입자가 입사 방향의 반대 방향으로 운동하게 된다는 것을 알 수 있다.
이제 정지해 있는 전자에 $\alpha$입자가 입사되어 충돌하는 상황을 생각해자. 그렇다면 $m_t=m_e$가 될 것이다.
각 입자의 질량은
$$m_e \approx 0.5~\text{MeV/c}^2,$$
$$m_\alpha \approx 4 \times 10^3~\text{MeV/c}^2$$
그러므로 두 입자의 질량비는
$$\frac{m_t}{m_\alpha} \approx 10^{-4}$$
이 된다. $\boldsymbol{v_\alpha}\cdot\boldsymbol{v_t}$이 양수가 되어 $\alpha$ 입자의 운동량 변화가 상당히 작을 것이다. 결론적으로 톰슨의 원자 모형으로 $\alpha$ 입자의 산란 실험을 하게 되면 $\alpha$ 입자의 산란 후 운동 방향이 산란 전 운동 방향과 거의 같아야 함을 알 수 있다. 하지만 실제 실험 결과 때때로 $\alpha$ 입자가 큰 각도로 산란되는 것이 관찰되었다. 이 문제를 해결하기 위해서 러더퍼드는 톰슨의 원자 모형이 아닌 다른 원자 모형을 생각했다. 그의 생각은 아래와 같았다.
러더퍼드의 원자 모형
- 원자의 중앙에는 양으로 대전된 입자가 있을 것이고 이 입자의 질량은 원자 질량의 대부분을 차지할 것이다.
- 전자는 위에 기술된 입자의 주변부를 원운동 할 것이다.
이러한 원자 모형을 생각한다면 $\alpha$ 입자의 산란 각도가 큰 현상은 꽤 자연스러운 결과가 된다. 예를 들어 과녁 입자가 금이라고 한다면 $$m_t = m_{Au} \approx 2\times10^5\text{MeV/c}^2,$$ 이 되어 $$\frac{m_t}{m_\alpha} \approx 50.$$ 이 된다. 그러므로 위 계산의 과정으로부터 $\alpha$입자는 큰 각도로 산란할 수 있음을 예상할 수 있다.