Table of Contents
바비네(Babinet)의 원리
불투명한 물체에 의한 프라운호퍼 회절 무늬가 그 물체 모양으로 생긴 슬릿에 의한 회절 무늬와 같다고 하는 원리. 단, 스크린 중앙부의 밝은 지점은 제외한다.
설명
보통 설명에서 생략되지만 기본적으로 아주 넓은 슬릿이 놓여있다고 생각하는 편이 이해하기 쉽다. 슬릿의 너비를 $a$라 하자. 아래 그림처럼 평면파가 들어오면 스크린에 비치는 회절 무늬의 폭은 $a$에 반비례하므로 스크린 중앙부의 매우 좁은 영역에 에너지가 집중될 것이다. 예를 들어 아래 그림에서 화살표로 표시된 부분은 스크린 중앙부에서 약간 벗어나 있으므로 어두울 것이다.
이제 넓었던 슬릿의 중앙부에 더 좁은 슬릿을 끼워넣자 (하늘색). 슬릿이 좁아졌으므로 회절 무늬는 넓어진다. 아까 화살표로 표시했던 스크린의 지점에 극대점이 만들어져 밝은 띠가 보인다고 가정하자.
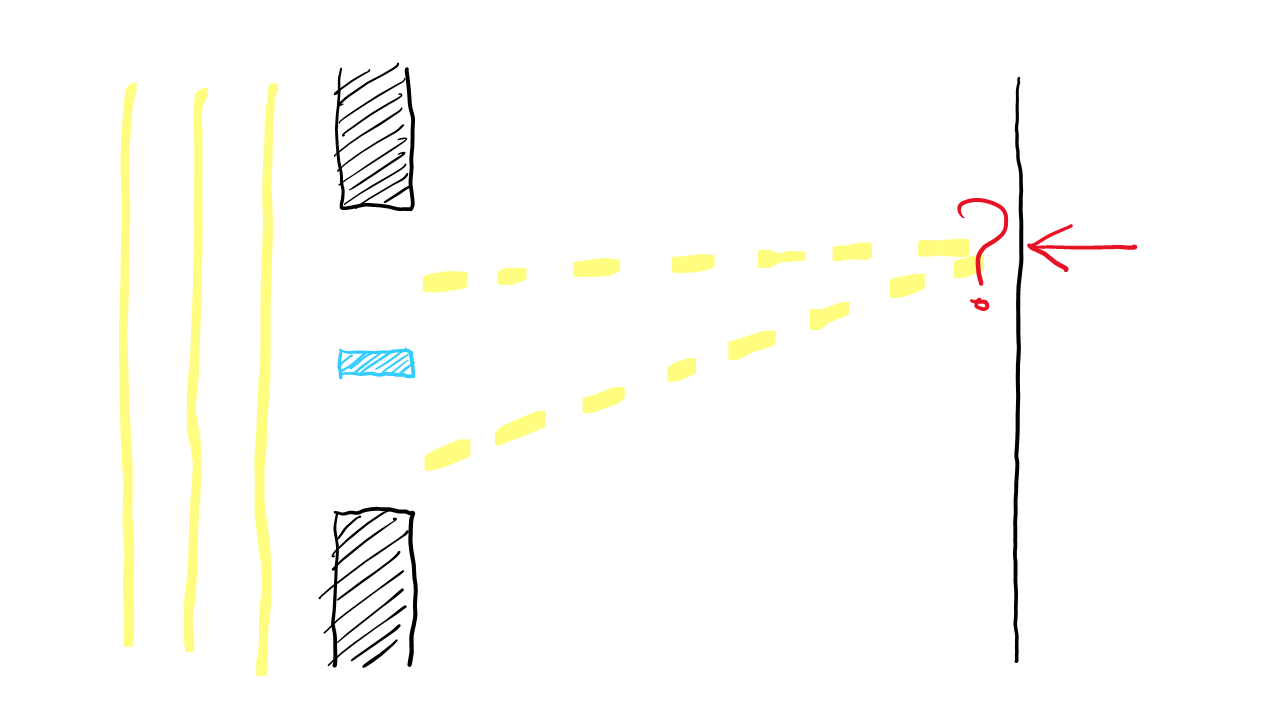
이제 좁은 슬릿을 빼고 슬릿 모양의 물체를 배치하자. 이 물체로 인한 회절 무늬는 어떠할지가 질문이다.
전자기파의 중첩을 생각해보면 마지막 두 그림의 빛을 합했을 때에 처음 그림의 결과가 나와야 할 것이다. 화살표 부분을 생각해보면 첫 번째 그림에서 그 지점이 어두웠으므로, 중첩의 결과는 상쇄간섭이어야 한다. 그리고 두 파동 사이에 상쇄간섭이 일어나기 위해서는 진폭이 같고 위상에서 $\pi$만큼의 차이가 나야 할 것이다.
우리가 스크린에서 회절 무늬의 밝고 어두움을 관찰할 때 위상 정보는 지워지며 빛의 강도는 진폭의 제곱으로부터 결정된다. 이는 마지막 그림 상황에서 화살표 부분의 밝기가 두 번째 그림에서의 밝기와 일치해야 한다는 것을 의미한다. 첫 번째 그림에서 어두웠던 부분 전부에 대해 같은 논리로, 물체에 의한 회절 무늬가 물체 모양 슬릿의 회절 무늬와 일치함을 논할 수 있다. 단, 첫 번째 그림에서 스크린 중앙부의 매우 좁은 영역은 밝았으므로 거기에서는 이 논리가 적용되지 않는다.
응용
머리카락에 레이저를 회절시켰을 때 생긴 회절 무늬는 그 머리카락 굵기만큼의 너비를 가진 단일 슬릿에 의한 회절 무늬와 같다. 따라서 레이저의 파장을 알고 머리카락으로부터 스크린까지의 거리를 잰다면 회절 무늬의 극소점 간격을 통해 머리카락의 굵기를 측정할 수 있다.