개요
원형 바퀴를 강체로 간주하고 바닥에서 미끄러짐 없이 굴러간다고 생각한다.
회전의 중심
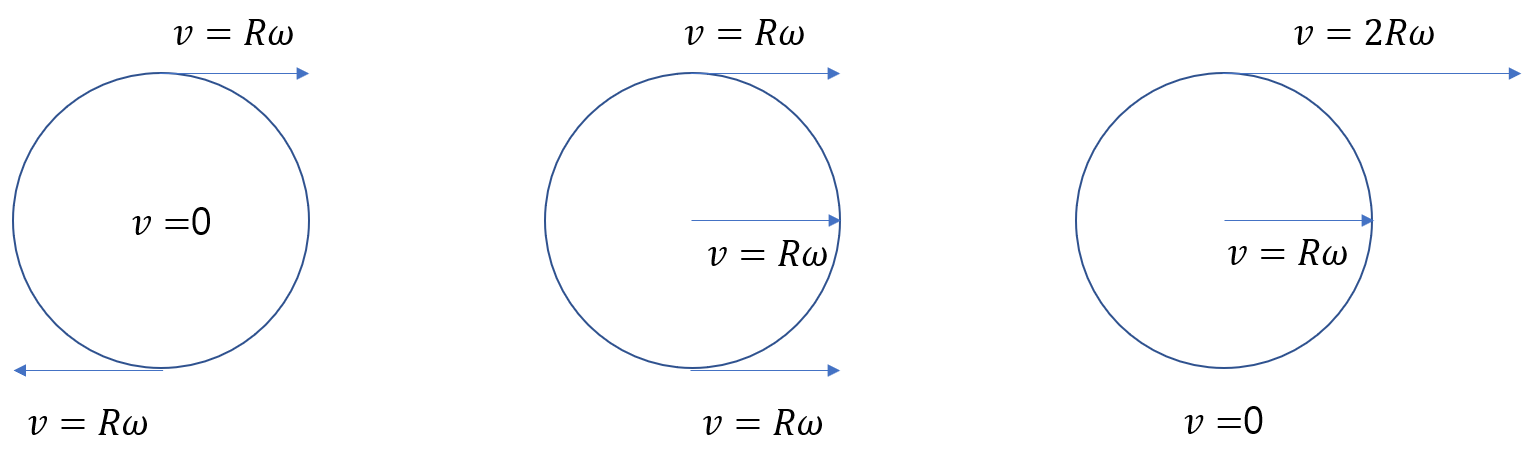
Serway & Jewett에 설명된 것처럼, 이 운동은 순수 회전 운동(아래 왼쪽 그림)과 순수 병진 운동(아래 가운데 그림)의 합으로 간주할 수 있다.
그런데 바닥 접촉점에서의 속력은 0, 거리 $R$만큼 떨어진 바퀴 중심에서는 $v=R\omega$, 그리고 바퀴 제일 윗단에서는 $v=2R\omega$이므로, 이 순간에는 바퀴가 바닥과의 접촉점을 중심으로 회전하고 있다고 말할 수도 있다.
이 점은 아래의 그림처럼 원을 정다각형의 극한으로 생각해보면 더욱 쉽게 이해할 수 있다.
이 접촉점 $P$를 중심으로 한 관성모멘트 $I_P$는 바퀴의 중심을 기준으로 한 관성모멘트 $I_\text{CM}$과 비교했을 때 $I_P = I_\text{CM}+MR^2$의 관계가 있다. 따라서 $P$를 중심으로 회전하는 회전 운동 에너지는 $$K = \frac{1}{2} I_P \omega^2 = \frac{1}{2}I_\text{CM} \omega^2 + \frac{1}{2} MR^2 \omega^2 = \frac{1}{2}I_\text{CM} \omega^2 + \frac{1}{2} M v^2$$ 으로서 질량중심 주위의 순수 회전 운동의 에너지, 그리고 회전 없이 순수 병진 운동하는 에너지로 쪼개어 쓸 수 있게 된다.
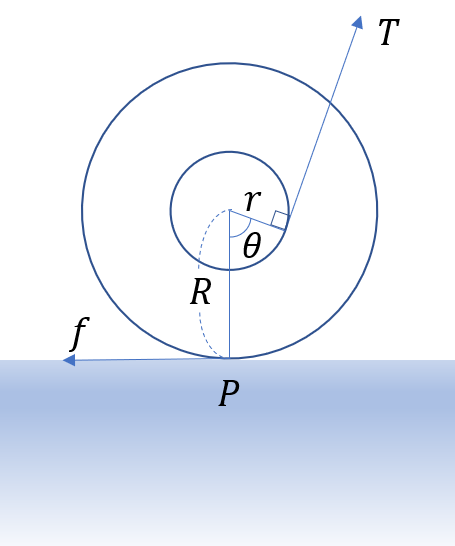
어떤 문제에서는 접촉점 $P$를 기준으로 생각하는 것이 훨씬 쉽게 옳은 답을 준다. 아래 그림은 (중심부 작은 원통에 실이 감겨 있는) 요요의 세 가지 상황을 보여주고 있다. 왼쪽 상황에서 요요가 오른쪽으로 굴러갈 것이라는 점은 비교적 쉽게 예상이 된다. 그렇다면 가운데 상황은 어떤가? 제일 오른쪽 상황처럼 실을 위로 잡아당긴다면, 요요를 구르지 않게끔 하는 각도는 어떻게 찾을 수 있을까? 그 평형점은 안정한가? 이들 문제는 접촉점을 기준으로 생각하는 것이 편리한 경우들이다.
분석을 위해 아래처럼 작은 반지름 $r$, 큰 반지름 $R$이며 질량이 $m$, 질량중심 주위로의 관성모멘트가 $I_\text{CM}$인 요요를 각도 $\theta$이고 크기 $T$인 장력으로 잡아당긴다고 하자.
오른쪽을 + 부호로 하는 수평방향의 병진운동에 관해서는 \begin{equation} T \cos\theta - f = ma \end{equation} 으로서 질량중심의 가속도 $a$를 얻고, 바퀴 중심을 축으로 하여 반시계방향을 +로 하는 회전운동에 관해서는 다음 식을 얻는다. \begin{equation} Tr-fR = I_\text{CM} \alpha. \end{equation} 미끄러짐이 없다고 하면 $a = -R\alpha$로 연결된다. 앞의 마이너스 부호는 바퀴가 오른쪽으로 구를 때 ($a>0$) 시계방향으로 회전해야 한다는 ($\alpha<0$) 방향성을 나타낸 것이다. $f$와 $\alpha$를 미지수로 놓고 풀어보면 \begin{equation} \alpha = \frac{T(r-R\cos\theta)}{(I_\text{CM}+mR^2)} \end{equation} 을 얻는다. 따라서 $r < R\cos\theta$일 때에 바퀴가 오른쪽으로 굴러가고, $r> R\cos\theta$이면 왼쪽, $r=R\cos\theta$이면 어느 쪽으로도 구르지 않는다. 이 마지막 등호 조건은 잡아당기는 줄을 연장한 선이 접촉점 $P$를 똑바로 가리킬 때에 만족된다. 이는 접촉점 $P$를 회전 중심으로 간주하면 곧바로 얻을 수 있는 결과이다.
요요 문제의 분석
힘과 토크
요요의 질량은 $m$이고 관성 모멘트는 $I$이며, $f$는 정지마찰력을 의미한다. $x$ 방향의 병진 운동을 기술하면 $$F_\text{net} = T-f = ma = mR\alpha$$ 이며 이때 $\alpha$는 각가속도이다. 이제 회전 운동을 기술하면 (편의상 시계방향을 +로 잡자) $$\tau_\text{net} = Tr + fR = I\alpha.$$ 이 두 개의 방정식을 연립하여 풀면 $$\alpha = \frac{T(R+r)}{I+mR^2}$$ 을 얻는다. 접촉점을 회전 중심으로 보고 풀 수도 있는데, 그럼 더욱 간단하다: $$\tau_\text{net} = T(R+r) = (I+mR^2)\alpha.$$
이 $\alpha$를 식에 다시 대입해 정지마찰력을 구해보면, $$f = \frac{T(I-mrR)}{I+mR^2}$$ 로서 $T$에 비례하는 값으로 구해진다. 만일 $T=0$이라면 $f$도 0이 되어 바퀴는 운동상태를 계속 유지할 것이다. 상황에 따라 $I<mRr$이면 (예를 들어 $I=\frac{1}{2}mR^2$이고 $r=R$) 마찰력은 $f<0$이 되어 $T$와 같은 방향일 수도 있게 된다.
일과 에너지
에너지의 측면에서, 정지마찰력이 바퀴에 하는 알짜 일은 0이다.
- 이를 보는 가장 쉬운 방법은, 앞에서처럼 원을 정다각형의 극한으로 보는 것이다. 힘이 작용하는 꼭지점은 바닥에 대해 움직이지 않으므로 일을 할 수 없다. (단, 정지마찰력이 하는 일이 언제나 0인 것은 아니다. 트럭에 짐을 싣고 트럭을 가속했을 때 트럭 바닥의 정지마찰력은 짐에 일을 한다.)
- 혹은 이렇게 생각할 수도 있다. 앞의 병진 운동 식에서 보듯이, 정지마찰력은 실제로 바퀴 질량중심의 가속도에 영향을 준다. 질량중심이 움직인 변위를 $L$이라고 하면 정지마찰력이 질량중심에 한 일은 $-fL$이다. 동시에, 정지마찰력은 바퀴 중심을 회전축으로 하여 회전 운동을 하게끔 토크를 준다. 바퀴가 각도 $\theta$만큼 돌았다면 정지마찰력이 이 회전에 한 일은 $fR\theta$이다. 미끄러짐이 없으므로 $L=R\theta$이고, 따라서 정지마찰력이 한 알짜 일은 $-fL + fR\theta = 0$이다. 그러므로 정지마찰력은 알짜 일을 하지 않고 단지 병진 운동의 에너지 일부를 회전 운동 에너지로 바꾸는 역할을 했다고 말할 수 있다.
- 혹은 그 반대로 회전 운동 에너지 일부를 병진 운동 에너지로 바꾸는 방향일 수도 있는데 ($f<0$이어서 정지마찰력이 회전을 감소시키는 경우에 해당할 것이다), 마찰이 없는 도로에서 바퀴를 돌리기 시작한 자동차를 상상해보자. 자동차는 앞으로 나아가지 못하고 엔진이 한 일은 모두 바퀴의 회전 운동 에너지로 갈 것이다. 정지마찰력의 존재가 이 회전 운동 에너지를 질량중심의 병진 운동 에너지로 바꾼다.
질량중심이 $v_{\text{CM},i}$의 속도로 움직이며 구르고 있는 요요를 생각하자. 반지름 $r$에 감겨있는 실을 장력 $T$로 잡아당겨 요요의 질량중심이 변위 $L$만큼을 이동했다면 그 동안 돌아간 각도는 $\theta = L/R$이고, 따라서 실이 $l = r\theta = (r/R)L$만큼 풀렸을 것이다. 실을 잡아당긴 힘이 한 일은 $W = T(L+l) = TL(1+r/R)$이다. 이 일이 요요의 병진 및 회전 운동 에너지 변화량이 된다. $$TL\left( 1+ \frac{r}{R} \right) = \left( \frac{1}{2}mv_{\text{CM}^2,f} + \frac{1}{2} I\omega_f^2 \right) - \left( \frac{1}{2}mv_{\text{CM}^2,i} + \frac{1}{2} I\omega_i^2 \right) = \left[ \frac{1}{2}mv_{\text{CM},f}^2 + \frac{1}{2} I \left(\frac{v_{\text{CM},f}^2}{R^2}\right) \right] - \left[ \frac{1}{2}mv_{\text{CM},i}^2 + \frac{1}{2} I \left(\frac{v_{\text{CM},i}^2}{R^2}\right) \right].$$ 이 식을 정리하면 질량중심의 나중 속력 $v_{\text{CM},f}$을 구할 수 있다. 질량중심이 가속도 $a_\text{CM} = (T-f)/m$로 등가속도 운동을 하고 있음을 생각해 분석해도 된다. $L$만큼 이동하는 데 걸리는 시간 $\Delta t$를 $L = v_{\text{CM},i} \Delta t + \frac{1}{2}a_\text{CM} \Delta t^2$을 통해 알아낸 다음 아래 식에 대입한다: $$v_{\text{CM},f} = v_{\text{CM},i} + a_\text{CM} \Delta t.$$ 이를 정리해보면 위와 동일한 결과이다.
잠김방지제동장치(Anti-lock Braking System, ABS)
위의 그림이 요요 대신 자동차 바퀴라고 생각하자. 실 대신에 브레이크 패드가 접촉하여 운동마찰력 $T$를 준다고 해도 위에서 적은 일-에너지 관계식의 좌변 $TL(1+r/R)$은 그대로 성립한다. 왜냐하면 운동마찰력이 질량중심의 변위 $L$만큼을 따라가며 작용하고, 거기에 더해 바퀴의 회전에 의한 접촉지점의 이동거리 $r\theta = L(r/R)$만큼도 추가적으로 일을 하기 때문이다.
비록 ABS의 일차적인 목적은 제동거리를 줄이는 것보다 차량의 방향 제어능력을 유지하는 데 있지만, 여기에서는 간단히 위의 결과를 사용하여 제동거리의 측면을 생각해보자. 초기속도 $v_{\text{CM},i}$는 주어진 값이고 바퀴가 최종적으로 정지해야 하므로 $v_{\text{CM},f}=0$이다. 따라서 $T$와 $L$은 다른 부호를 가지며, $L$의 크기, 즉 제동거리를 최소화하기 위해서는 $T$의 크기를 최대한 증가시켜야 한다.
그런데 바닥이 주는 정지마찰력 $f$가 $T$에 비례하기 때문에, $T$가 지나치게 커지면 $f$가 바닥의 최대정지마찰력을 넘어설 수 있다. 이는 바퀴가 바닥으로부터 미끄러진다는 뜻이다. 극단적으로 바퀴가 잠겨버리면 그때부터 운동 에너지 소모는 바닥과 바퀴 사이 운동마찰력이 하는 일에 의해 일어난다 (바퀴가 잠기기 전까지는 둘 사이에 정지마찰력이 작용하고 있었다). 반면 바퀴와 브레이크 패드 사이에는 상대 운동이 없으므로 바퀴 질량중심의 운동 에너지를 줄이는 일을 브레이크 패드는 더 이상 하지 못한다.
참고문헌
- Serway and Jewett, 대학물리학(Physics for Scientists and Engineers with Modern Physics) 10판 (북스힐, 2019), 예제 10.14.