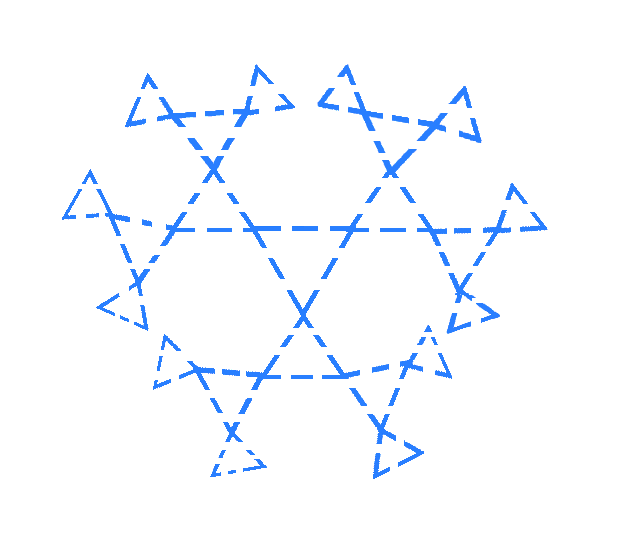
Kagome 격자는 다음 그림과 같은 구조를 갖는다.

이러한 Kagome 격자에서, 다음과 같은 해밀토니안을 갖는 이징 모형을 고려하자.

$$ \mathcal{H}=-J_3 \sum_{\Delta}\sigma_i \sigma_j \sigma_k -J_2\sum _{\text{n.n}}\sigma_i \sigma_j - h\sum_i \sigma_i $$

첫 번째 항은 $i,j,k$의 마디가 이루는 삼각형에 대한 상호작용이고, 두 번째 항은 가장 근접한 이웃(nearest neighbor) 쌍에 대한 상호작용이며, 마지막 항은 각 마디의 스핀과 자기장에 대한 항이다.

$$ \\ $$ Kagome 격자에 대해서 정확한 해와 다이어그램을 얻은 논문은 첫 번째 참고문헌에 해당한다.

다만, (일종의 근사법으로서) Husimi 트리(tree) 구조에서의 이징 모형에 대해서 풀이한 뒤, 그 결과를 이용해서 kagome 격자 구조에서의 결과를 이해하는 방법도 있다.

Husimi 트리는 다음과 같은 구조이다. ($\gamma-1$개의 삼각형을 각 노드에 붙이는 방식으로 구성되며, 그림에서는 $\gamma=2$이다.)

우선, Husimi tree 구조에서의 '국소적 자화량(local magnetization)'을 다음과 같이 쓰자.

$$ \langle \sigma_0 \rangle = \sum_\sigma \sigma_0 P(\sigma) /Z$$ 이때, 분배함수 $Z=\sum_\sigma P(\sigma)$ 이다. $P(\sigma)$는 아래와 같이 표현된다.

$$ P(\sigma ) = \exp\left[\beta\bigg\{J_3 \sum_{\Delta}\sigma_i \sigma_j \sigma_k + J_2 \sum_{\text{n.n}}\sigma_i\sigma_j + h\sum_i \sigma_i \bigg\}\right]$$

이때, Husimi tree의 구조에 대하여 다음의 식을 정의해보자.

$$ g_n(\sigma_0) = \sum_{\{\sigma_1\}} \exp\Bigg[\beta\Bigg(J_3\sum_\Delta \sigma_0\sigma_1^{(1)} \sigma_1^{(2)} + J_2 \sum_{\text{n.n}}\sigma_0 \sigma_1 + h \sum _{j=1,2}\sigma_1^{(j)} \Bigg) \Bigg][g_{n-1}(\sigma_1^{(1)})]^{\gamma-1}[g_{n-1}(\sigma_1^{(2)})]^{\gamma-1} $$

여기서 $\sigma_1^{(j)}$은 sub-tree 중 ($\sigma_0$을 제외한) $j$ 번째에 연결되어 있는 스핀을 가리키는 표현이다.

$$ \\ $$ 이러한 방식의 정의는 Husimi 트리가 트리 구조를 가지기에 가능한 것이다. 그에 따라, 분배함수 $Z=\sum_\sigma P(\sigma)$를 다음과 같이 적을 수 있다.

$$ Z = \sum_{\sigma_0} \exp(\beta h\sigma_0) [g_n(\sigma_0)]^{\gamma} $$

따라서,

$$ \langle \sigma_0 \rangle = Z^{-1} \sum_{\sigma_0} \sigma_0 \exp (\beta h\sigma_0 )[g_n(\sigma_0)]^{\gamma} $$ 로 쓸 수 있다.

$$ \\ $$

이때, $z_n$이라는 값을 아래와 같이 정의하자.

$$ z_n = g_n(+)/g_n(-) $$

그렇다면 $\langle \sigma_0 \rangle$는 다음과 같이 쓰여진다.

$$ \begin{align} \langle \sigma_0 \rangle &= \frac{\sum_{\sigma_0}\sigma_0 \exp(\beta h\sigma_0) [g_n(\sigma_0)]^{\gamma}}{Z} \\ &= \frac{e^{\beta h}g_n(+)^{\gamma}\ - \ e^{-\beta h}g_n(-)^{\gamma}}{e^{\beta h}g_n(+)^{\gamma}\ + \ e^{-\beta h}g_n(-)^{\gamma}} \\ &= \frac{e^{2\beta h}g_n(+)^{\gamma} \ -g_n(-)^{\gamma}}{e^{2\beta h}g_n(+)^{\gamma} \ +g_n(-)^{\gamma}} \\ &= \frac{az_n^{\gamma} \ -1}{az_n^{\gamma} \ +1} \end{align} $$ 여기에서 $a=e^{2\beta h}$ 이다.

$$\\ $$

$z_n$에 대해서는 $g_n(\sigma_0)$의 식을 사용해서 map을 얻을 수 있다.

우선, 앞서 살펴본

$$ g_n(\sigma_0) = \sum_{\{\sigma_1\}} \exp\Bigg[\beta\Bigg(J_3\sum_\Delta \sigma_0\sigma_1^{(1)} \sigma_1^{(2)} + J_2 \sum_{\text{n.n}}\sigma_0 \sigma_1 + h \sum _{j=1,2}\sigma_1^{(j)} \Bigg) \Bigg][g_{n-1}(\sigma_1^{(1)})]^{\gamma-1}[g_{n-1}(\sigma_1^{(2)})]^{\gamma-1} $$

의 식에서, $g_n(+)$와 $g_n(-)$를 다음과 같이 구하는 것이다.

$$ \begin{align} g_n(+) &= e^{\beta(J_3+3J_2+2h)}g_{n-1}^{(\gamma-1)}(+)g_{n-1}^{\gamma -1}(+) \\ &\ \ + 2e^{\beta(-J_3+J_2)}g_{n-1}^{(\gamma-1)}(+)g_{n-1}^{\gamma -1}(-) \\ &\ \ +e^{\beta(J_3 - J_2 -2h)}g_{n-1}^{(\gamma-1)}(-)g_{n-1}^{\gamma -1}(-), \\ \\ g_n(-) &= e^{\beta(-J_3 -J_2 +2h)}g_{n-1}^{(\gamma-1)}(+)g_{n-1}^{\gamma -1}(+) \\ &\ \ + 2e^{J_3-J_2}g_{n-1}^{(\gamma-1)}(+)g_{n-1}^{\gamma -1}(-) \\ &\ \ + e^{\beta(-J_3 +3J_2 -2h)}g_{n-1}^{(\gamma-1)}(-)g_{n-1}^{\gamma -1}(-). \end{align} $$ 그리고, $z_n=g_n(+)/g_n(-)$를 다음과 같이 구할 수 있다.

$$ z_n = \frac{e^{\beta(J_3+3J_2+2h)}z_{n-1}^{2(\gamma-1)} + 2e^{\beta(-J_3 + J_2)}z_{n-1}^{\gamma-1} +e^{\beta(J_3 - J_2 -2h)}} {e^{\beta(-J_3 -J_2 +2h)}z_{n-1}^{2(\gamma-1)} + 2e^{\beta(J_3-J_2)}z_{n-1}^{\gamma-1} + e^{\beta(-J_3 +3J_2 -2h)}} $$

위의 식은 분모와 분자에 $g_{n-1}^{(\gamma-1)}(-)g_{n-1}^{\gamma -1}(-)$를 나누어준 결과이다.

또한, 다음과 같은 변수들을 새로 정의하고

$$ a= e^{2\beta h},\ b=e^{2\beta J_2 },\ c=e^{2\beta J_3} $$

$z_n$을 다음과 같이 정리하자.

$$ z_n = \frac{c^{1/2}b^{3/2}a z_{n-1}^{2(\gamma-1)} + 2c^{-1/2}b^{-1/2}z_{n-1}^{\gamma -1}+ c^{1/2}b^{-1/2}a^{-1}}{c^{-1/2}b^{-1/2}az_{n-1}^{2(\gamma-1)} +2c^{1/2}b^{-1/2}z_{n-1}^{\gamma-1}+c^{-1/2}b^{3/2}a^{-1}} $$

$$ \\ $$

$$ = \frac{a^2b^2c z_{n-1}^{2(\gamma-1)} + 2az_{n-1}^{\gamma -1}+ c}{a^2z_{n-1}^{2(\gamma-1)} +2acz_{n-1}^{\gamma-1}+b^2}. $$

위의 식의 마지막 등식은 분모와 분자에 $c^{-1/2}b^{-1/2}a^{-1}$을 나누어줌으로써 얻었다.

$$ \\ $$

따라서 우리는 $z_n$에 대하여 다음의 map을 얻은 것이다.

$$z_n=f(z_{n-1}), \quad f(z) = \frac{a^2b^2cz^{2(\gamma-1)}+2az^{\gamma-1}+c}{a^2z^{2(\gamma-1)} + 2acz^{\gamma-1} +b^2}$$

$$ \\ $$ 만약 각각의 삼각형에 대한 상호작용(three-spin interaction)만 존재하는 모형이라면, map은 아래와 같이 쓰인다.

$$ f(z) = \frac{cz^{2(\gamma-1)}+2z^{\gamma-1}+c}{z^{2(\gamma-1)} + 2cz^{\gamma-1} +1}$$

위에서 얻은 map에서 $\gamma=2$를 대입한 경우는 kagome 격자에서의 이징 모형을 잘 근사하는 경우이다.

그 경우, map은 아래와 같다.

$$ f(z) = \frac{cz^2 +2z +c}{z^2 + 2cz +1}$$

이러한 map에 대해서 $z=f(z)$를 풀면 고정점(fixed point)을 얻을 수 있고, (직접 풀이하거나 Mathematica를 이용하여) 다음과 같이 얻을 수 있다.

$$ \\ $$ $c=e^{2\beta J_3} $으로서 $c$는 음수가 아니므로 $-c$는 양수가 아니다.

이때, $z_n=\frac{g_n(+)}{g_n(-)}$의 $g_n(\sigma)$는 지수함수(exponential)의 합의 형태로 표현된다는 것에 유의하면

$z=f(z)$의 해는 (음수가 아닌) 양수임을 알 수 있다.

따라서, 위의 3가지 고정점 중 $z=1$만이 유일하게 가능한 경우이다.

$$ \\ $$ 그러한 $z=1$이 안정적인(stable) 고정점인지, 아래와 같이 확인해보면

(초기의 $z$값에 무관하게) map을 수 차례 거친다면 $z=1$의 고정점으로 가게 된다.

$$ \\ $$ 이를 통해, $$ \begin{align} \langle \sigma_0 \rangle= \frac{az_n^{\gamma} \ -1}{az_n^{\gamma} \ +1} \end{align} $$ 에서 $\gamma=2$와 $a=1$, $z^*=1$ 을 대입하면 $\langle \sigma_0 \rangle =0$인 것을 확인할 수 있다.

$$\\$$ 따라서, kagome 격자 위의 이징 모형의 해밀토니안이 각각의 삼각형에 대한 상호작용(three-spin interaction)만 포함한다면

자화량의 기댓값이 $0$이라는 것을 위와 같은 근사를 통해 알아낼 수 있다.

$$ \\ $$

1. Exact results for lattice models with pair and triplet interactions, X N Wu and F Y Wu, 1989.

2. Phase diagrams of Ising models on Husimi trees II. Pair and multisite interaction systems, James L. Monroe, 1992.

3. Thermodynamic approach to three-site antiferromagnetic Ising model in chaotic region, N.S. Ananikian and S.K. Dallakian, 2018.