Table of Contents
1차원 이징 사슬
주기적인 경계조건을 갖는 1차원 이징 사슬을 생각했을 때, 계의 해밀토니안을 다음과 같이 나타낼 수 있다. $$\tilde{H}=-J\sum\limits_{i=1}^{N}\sigma_{i}\sigma_{i+1}-\tilde{h}\sum\limits_{i=1}^{N}\sigma_{i}$$ 이 때, $\sigma_{i}=\pm1$이고 사슬의 주기성에 의해 $\sigma_{N+1}=\sigma_{1}$이 된다. $-\beta(=-\frac{1}{k_{B}T})$를 해밀토니안에 곱하여 차원이 없는 해밀토니안 $H$를 정의하면
\begin{equation}\notag
\begin{split}
H=-\beta\tilde{H}&=K\sum\limits_{i=1}^{N}\sigma_{i}\sigma_{i+1}+h\sum\limits_{i=1}^{N}\sigma_{i}\qquad (K=\beta J,\, h=\beta\tilde{h}) \\
&=K(\sigma_{1}\sigma_{2}+\sigma_{2}\sigma_{3}+\cdots+\sigma_{N}\sigma_{1})+h(\sigma_{1}+\sigma_{2}+\cdots+\sigma_{N})\\
&=K(\sigma_{1}\sigma_{2}+\sigma_{2}\sigma_{3}+\cdots+\sigma_{N}\sigma_{1})+\frac{h}{2}\left[(\sigma_{1}+\sigma_{2})+(\sigma_{2}+\sigma_{3})+\cdots+(\sigma_{N}+\sigma_{1})\right] \\
&=\sum\limits_{i=1}^{N}\left[K\sigma_{i}\sigma_{i+1}+\frac{h}{2}(\sigma_{i}+\sigma_{i+1})\right]
\end{split}
\end{equation}
이 된다. 이 경우, 분배함수는
$$Z_{c}=\underset{\{a_{i}\}}{\mathrm{Tr}}e^{H}=\sum\limits_{\{\sigma_{i}\}=\pm1}\exp\left\{\sum\limits_{i=1}^{N}\left[K\sigma_{i}\sigma_{i+1}+\frac{h}{2}(\sigma_{i}+\sigma_{i+1})\right]\right\}$$
로 쓰이고, 자유도에 대한 합은
$$\sum_{\{{\sigma_{i}\}}=\pm1}e^{H}=\sum_{{\sigma_{2}}=\pm1}\sum_{{\sigma_{4}}=\pm1}\cdots\sum_{{\sigma_{N}}=\pm1}\left[\sum_{{\sigma_{1}}=\pm1}\sum_{{\sigma_{3}}=\pm1}
\cdots\sum_{{\sigma_{N-1}}=\pm1}e^{H}\right]$$
로 나타낼 수 있다. $H$에서 $\sigma_{1}$을 포함하는 항을 보기 위해 $i=1$인 경우와 $i=N$인 경우를 더해보면
$$K\sigma_{1}(\sigma_{N}+\sigma_{2})+h\sigma_{1}+\frac{h}{2}(\sigma_{N}+\sigma_{2})$$이 되고 여기서 $\sigma_{1}$이 포함된 항에 대해서만 생각해보자.
$\sigma_{1}$의 가능한 모든 값을 합하면
$$\sum_{\sigma_1=\pm1}e^{K\sigma_1(\sigma_N+\sigma_2)+h\sigma_1} = 2\cosh\left[K(\sigma_N+\sigma_2)+h\right]$$
이 된다. $\sigma^{2n}=1,\,\sigma^{2n+1}=\sigma$임을 이용하여 식을 좀 더 정리해보면
\begin{align*}
\sum_{\sigma_1=\pm1}e^{K\sigma_1(\sigma_N+\sigma_2)+h\sigma_1+h(\sigma_N+\sigma_2)/2} &= 2e^{h(\sigma_N+\sigma_2)/2}\cosh\left[K(\sigma_N+\sigma_2)+h\right]\\
&= \exp\left\{2g + K^\prime\sigma_N\sigma_2 + \frac{1}{2}h^\prime(\sigma_N+\sigma_2)\right\}
\label{renorm}
\end{align*}
로 나타낼 수 있다. 여기서
$$K^{\prime}=\frac{1}{4}\ln\frac{\cosh(2K+h)\cosh(2K-h)}{\cosh^{2}h},$$
$$h^{\prime}=h+\frac{1}{2}\ln\frac{\cosh(2K+h)}{\cosh(2K-h)},$$
$$g=\frac{1}{8}\ln\left[16\cosh(2K+h)\cosh(2K-h)\cosh^{2}h\right]$$
이다. $\sigma_{3},\sigma_{5},\ldots,\sigma_{N-1}$이 각각 위와 같은 결과를 가지므로
\begin{equation}\notag
\sum\limits_{\sigma_{1},\sigma_{3},\ldots,\sigma_{N-1}}e^{H}=\exp\left\{{Ng(K,h)+K^{\prime}\sum\limits_{i}\sigma_{2i}\sigma_{2i+2}+h^{\prime}\sum\limits_{i}\sigma_{2i}}\right\}
\end{equation}
을 얻게 된다. 이 결과를 $\sum_\limits{\{\sigma_i\}=\pm1}e^{H}$에 대입하면
\begin{equation}\notag
\sum_{\{\sigma_i\}=\pm1}e^H=\sum_{\sigma_2=\pm1}\sum_{\sigma_4=\pm1}\cdots\sum_{\sigma_N=\pm1}\exp\left\{{Ng(K,h)+K^{\prime}\sum\limits_{i}\sigma_{2i}\sigma_{2i+2}+h^{\prime}\sum\limits_{i}\sigma_{2i}}\right\}
\end{equation}
이 된다. 결과식의 형태를 보면 짝수번째 스핀에 대한 합이 분배함수 $Z_{c}$와 닮은 형태를 가지는 것을 알 수 있다. 이것은 처음의 물리계가 짝수번째 스핀들이 자기장 $h^{\prime}$ 속에서 결합계수 $K^{\prime}$로 가장 가까이 있는 스핀들과 상호작용하는 물리계로 치환될 수 있음을 보여준다. 그러므로 처음의 분배함수는
\begin{equation}\notag
Z_{c}(N,K,h)=e^{Ng(N,h)}Z_{c}\left(\frac{N}{2},K^{\prime},h^{\prime}\right)
\end{equation}
로 나타내어질 수 있다. 위와 같은 과정을 재규격화 과정이라 한다. 이 과정은 똑같은 방법으로 계속될 수 있기 때문에
\begin{equation}\notag
\begin{split}
Z_{c}(N,K,h)&=e^{Ng(N,h)}Z_{c}\left(\frac{N}{2},K^{\prime},h^{\prime}\right) \\
&=e^{Ng(K,h)+\frac{N}{2}g(K^{\prime},h^{\prime})}Z_{c}\left(\frac{N}{4},K^{\prime\prime},h^{\prime\prime}\right) \\
&=e^{Ng(K,h)+\frac{N}{2}g(K^{\prime},h^{\prime})+\frac{N}{4}g(K^{\prime\prime},h^{\prime\prime})}Z_{c}\left(\frac{N}{8},K^{\prime\prime\prime},h^{\prime\prime\prime}\right) \\
&=\cdots
\end{split}
\end{equation}
로 나타낼 수 있다. 이런 관계를 통해 자유에너지에 대한 식
\begin{equation}\notag
-\beta G(N,K,h)=\ln Z_{c}(N,K,h)=Ng(K,h)+\ln Z_{c}\left(\frac{1}{2}N,K^{\prime},h^{\prime}\right)
\end{equation}
이 아래와 같이 정리될 수 있다.
\begin{equation}\notag
\begin{split}
-\frac{\beta G(N,K,h)}{N}&=f(K,h) \\
&=g(K,h)+\frac{1}{2}g(K^{\prime},h^{\prime})+\frac{1}{4}g(K^{\prime\prime},h^{\prime\prime})+\cdots \\
&=\sum\limits_{j=0}^{\infty}\left(\frac{1}{2}\right)^{j}g(K_{j},h_{j})
\end{split}
\end{equation}
이제 위 결과가 수렴하는지 알아보기 위해 자기장 $h$와 결합계수 $K$가 어떻게 변화해가는지 그 흐름을 살펴보자. $h=0$인 경우를 생각해보면 이 경우, $K^{\prime}$은 위 식으로부터
$$K^{\prime}=\frac{1}{2}\ln\cosh2K\leq K$$
임을 알 수 있다. 등호는 $K=0(T=\infty),\,K=\infty(T=0)$에 성립하며 이 경우는 고정점이 된다. 결합계수 $K$ 공간에서 $K$의 값은 재규격화 과정이 진행됨에 따라 $K=\infty$에서 $K=0$으로 변해감을 알 수 있다. 그러므로 $K=0$이 안정 고정점, $K=\infty$가 불안정 고정점이 되며 위의 급수가 유한한 $h=0$일 때 유한한 $K$에 대해 수렴함을 알 수 있다. 계속해서 $h=0$인 경우의 $g$와 $f$의 값을 살펴보자. $g$의 값은
$$g(K,0)=\frac{1}{2}\ln2+\frac{1}{4}\ln(\cosh2K)$$
이고 $K$의 값이 작아질수록 우변의 두 번째 항이 $0$에 가까워진다는 것을 알 수 있다. 두 번째 항을 무시할 수 있는 적당한 항이 $n$번 째 항이라고 하면 위의 급수에서 $j>n$인 경우 $g(K,0)=\frac{1}{2}\ln2$로 나타낼 수 있기 때문에 $f(K,0)$을 다음과 같이
$$f(K,0)=\sum\limits_{j=0}^{n}g(K_{j},0)\left(\frac{1}{2}\right)^{j}+2^{-(n+1)}\ln2$$
쓸 수 있다.
이제 $h\neq0$인 경우를 살펴보면 $h^{\prime}=h+\frac{1}{2}\ln\frac{\cosh(2K+h)}{\cosh(2K-h)}$이므로 $K\neq\infty$인 모든 $K$에 대하여
$$\frac{\partial h^{\prime}}{\partial h}>1$$
이 된다는 것을 확인할 수 있다. 결론적으로 재규격화 과정이 진행될수록 처음의 물리계는 $K$의 값은 점점 작아져 $K=0$에 가까워지고 $h$의 값은 점점 더 커지는 물리계로 치환된다고 할 수 있다.
$\\$ $\\$ $\\$ 앞서 설명된 '재규격화'는 크게 2가지의 과정으로 나뉘는데,
하나는 coarse graining 과정, 다른 하나는 rescaling 이다.
coarse graining은 '대충 갈기' 또는 '대충 뽑기' 라고 번역할 수 있는데, 이러한 의미를 잘 이해하기 위해
아래의 '블록 스핀 (block spin)'에 대한 설명을 보자.
블록 스핀 (Block spin)
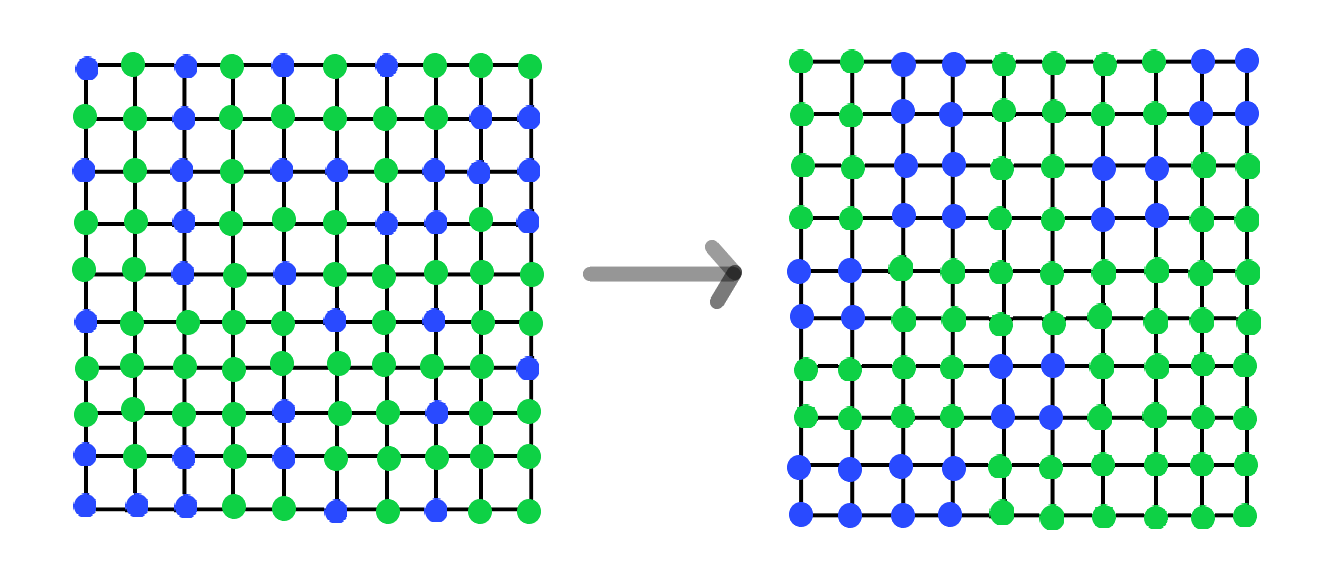
아래의 그림 중 왼쪽은, 어느 특정 시점에서 10×10개의 2차원 이징 모형 스핀 배열의 원본이고, 오른쪽 그림은 그러한 왼쪽의 배열을 '블록 스핀'의 개념을 이용하여 수행한 변환을 표현한 것이다.
(이해를 돕기 위해 그림판을 이용하여 간단히 그려보았다. 실제로는 랜덤하게 그린 것은 아니다.)
블록 스핀이란, 여러 스핀들을 묶어서 하나의 스핀으로 대체하여 본 스핀을 말한다.
즉, 위의 경우는 아래의 방식으로, 2×2 정사각형 안에 들어있는 스핀들을 하나로 묶은 후
그 2×2 정사각형 내의 왼쪽 아래에 위치한 스핀의 부호를 택하여, 나머지 3개의 스핀까지 같은 스핀으로 둔 방식이다.
이러한 방식을 'decimation'이라고 한다. 특정한 같은 방식으로 한 개의 스핀 부호를 택하고 나머지 스핀들의 정보는 '지우는' 방법이기 때문이다.
다른 변환 방식으로는 'majority rule'이 있다. 한 블록 스핀 내에서 '다수'의 스핀이 향하는 방향(부호)를 블록 스핀의 부호로 택하는 방법이다.
그래서 이러한 과정을 coasre graining이라고 부르는데, 기존 스핀들의 정보가 보다 '대충' 갈아졌기 때문(연마) 으로 이해할 수 있다.
$\\$ $\\$ 같은 방식으로 128×128개의 스핀 배열을 예로 들어, 아래의 그림들로 보다 명확히 살펴볼 수 있다.
(각각 '초기의 스핀배열의 원본 (앞쪽 첫번째), 블록 스핀 (앞쪽 두번째)' , '100 MC steps가 지난 상태의 원본 (뒤쪽 첫번째), 블록 스핀 (뒤쪽 두번째)')$\\$

 $\\$ $\\$ $\\$ $\\$
$\\$ $\\$ $\\$ $\\$


($\beta=0.5$ 로 설정하였고, 편의상 $J$=1 로 두었다.)
위에서 설명한 decimation의 방식을 택하여 시뮬레이션을 수행해 보기 위해, 아래의 C++ 코드를 이용할 수 있으며,
자발적 대칭 깨짐(spontaneous symmetry breaking)에서 수행한 기존의 코드에서 decimation을 이용하는 부분만 추가해주었다.
(spin : 스핀 배열 원본, deci : decimation을 적용시킨 블록 스핀 배열)
#include <iostream> #include <cstdlib> #include <cmath> #include <random> #include <vector> using namespace std; int main() { const int lsize=30; const float beta = 0.5; const float J = 1; const int MC_steps=1000; const int iter=lsize*lsize*5000; int i; int j; float del_E; float mp_probability; // mp means metropolis float spin[lsize][lsize] = { 0 }; float deci[lsize][lsize] = { 0 }; random_device rd; mt19937 gen(rd()); bernoulli_distribution distrib(0.5); uniform_int_distribution<> distri(0, lsize - 1); uniform_real_distribution<> dist(0, 1); for (int t=0; t<iter;t++){ if (t==0){ for (int a=0;a<lsize;a++){ for (int b=0;b<lsize;b++){ if (distrib(gen)){ spin[a][b]=1; } else { spin[a][b]=-1; } } } } else { i = distri(gen); j = distri(gen); if (i<lsize-1 && j<lsize-1){ del_E=2*J*(spin[i][j]*(spin[i-1][j] + spin[i+1][j] + spin[i][j-1] + spin[i][j+1])); // periodic boundary condition } else if (i==lsize-1 && j<lsize-1){ del_E=2*J*(spin[i][j]*(spin[i-1][j] + spin[0][j] + spin[i][j-1] + spin[i][j+1])); } else if (i<lsize-1 && j==lsize-1){ del_E=2*J*(spin[i][j]*(spin[i-1][j] + spin[i+1][j] + spin[i][j-1] + spin[i][0])); } else if (i==lsize-1 && j==lsize-1){ del_E=2*J*(spin[i][j]*(spin[i-1][j] + spin[0][j] + spin[i][j-1] + spin[i][0])); } if (exp(-beta*del_E) < 1){ mp_probability = exp(-beta*del_E); } else if (exp(-beta*del_E) >= 1) { mp_probability = 1; } if (dist(gen) < mp_probability){ spin[i][j] = spin[i][j]*(-1); } } for (int a=0;a<lsize;a++){ for (int b=0;b<lsize;b++){ if ((a+1)%2==0 && (a+b)%2==1){ deci[a][b] = spin[a][b]; deci[a][b+1] = spin[a][b]; deci[a-1][b+1] = spin[a][b]; deci[a-1][b] = spin[a][b];//decimation (for block spin) } } } } return 0; }
참고문헌
- M. Plischke and B. Bergersen, Equilibrium Statistical Physics, 2nd ed.(World Scientific, Singapore, 1994)