재규격화 (Renormalization)
'재규격화'는 크게 2가지의 과정으로 나뉘는데,
하나는 coarse graining 과정, 다른 하나는 rescaling 이다.
coarse graining은 '거친(coarse) 결정화(graining)' 또는 '거친 연마 과정' 이라고 해석할 수 있는데, 이러한 의미를 잘 이해하기 위해
아래의 '블록 스핀 (block spin)'에 대한 설명을 보자.
블록 스핀 (Block spin)
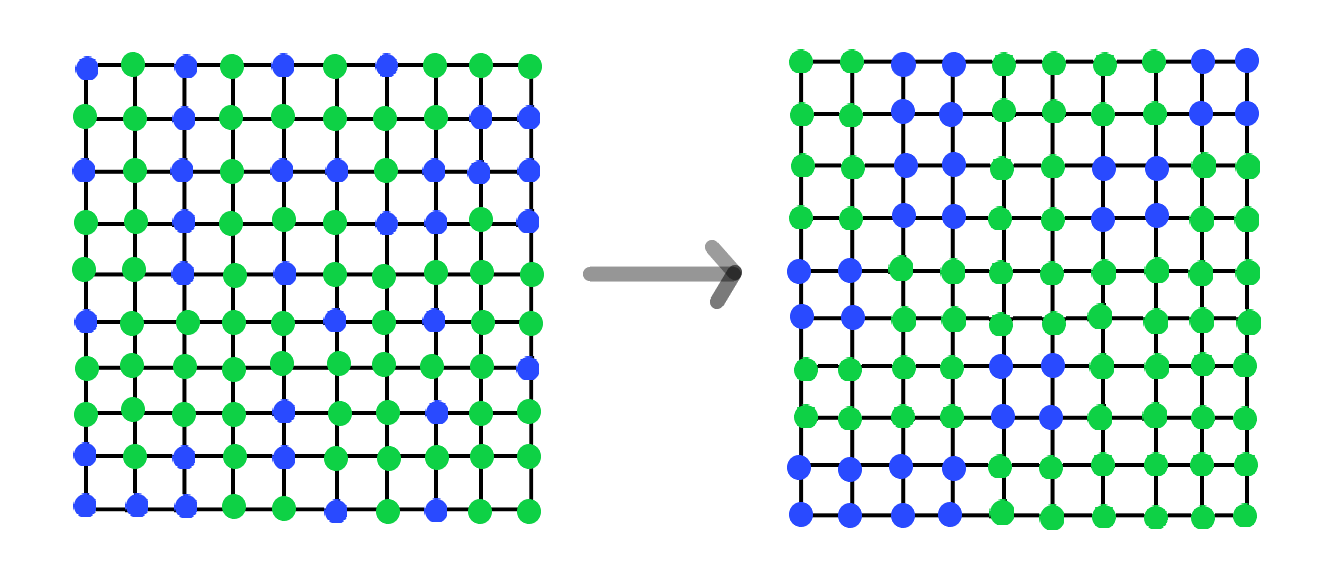
아래의 그림 중 왼쪽은, 어느 특정 시점에서 10×10 스핀 배열의 원본이고, 오른쪽 그림은 그러한 왼쪽의 배열을 '블록 스핀'의 개념을 이용하여 변환한 것 이다.
블록 스핀이란, 여러 스핀들을 묶어서 하나의 스핀으로 대체하여 본 스핀을 말한다.
즉, 위의 경우는 아래의 방식으로, 2×2 정사각형 안에 들어있는 스핀들을 하나로 묶은 후
그 2×2 정사각형 내의 왼쪽 아래에 위치한 스핀의 부호를 택하여, 나머지 3개의 스핀까지 같은 스핀으로 둔 방식이다.
이러한 방식을 'decimation'이라고 한다. 특정한 같은 방식으로 한 개의 스핀 부호를 택하고 나머지 스핀들의 정보는 '지우는' 방법이기 때문이다.
다른 변환 방식으로는 'majority rule'이 있다. 한 블록 스핀 내에서 '다수'의 스핀이 향하는 방향(부호)를 블록 스핀의 부호로 택하는 방법이다.
그래서 이러한 과정을 coasre graining이라고 부르는데, 기존 스핀들의 정보가 '보다 거칠게' 연마 되었기 때문으로 이해할 수 있다.
$\\$ $\\$ 같은 방식으로 128×128개의 스핀 배열을 예로 들어, 아래의 그림들로 보다 명확히 살펴볼 수 있다.
(각각 '초기의 스핀배열의 원본 (왼쪽), 블록 스핀 (오른쪽)' , '100 MC steps가 지난 상태의 원본 (왼쪽), 블록 스핀 (오른쪽)')$\\$

 $\\$
$\\$


($\beta=0.5$ 로 설정하였고, 편의상 $J$=1 로 두었다.)
위에서 설명한 decimation의 방식을 택하여 시뮬레이션을 수행해 보기 위해, 아래의 C++ 코드를 이용할 수 있으며,
자발적 대칭 깨짐(spontaneous symmetry breaking)에서 수행한 기존의 코드에서 decimation을 이용하는 부분만 추가해주었다.
(spin : 스핀 배열 원본, deci : decimation을 적용시킨 블록 스핀 배열)
#include <iostream> #include <cstdlib> #include <cmath> #include <random> #include <vector> using namespace std; int main() { const int lsize=30; const float beta = 0.5; const float J = 1; const int MC_steps=1000; const int iter=lsize*lsize*5000; int i; int j; float del_E; float mp_probability; // mp means metropolis float spin[lsize][lsize] = { 0 }; float deci[lsize][lsize] = { 0 }; random_device rd; mt19937 gen(rd()); bernoulli_distribution distrib(0.5); uniform_int_distribution<> distri(0, lsize - 1); uniform_real_distribution<> dist(0, 1); for (int t=0; t<iter;t++){ if (t==0){ for (int a=0;a<lsize;a++){ for (int b=0;b<lsize;b++){ if (distrib(gen)){ spin[a][b]=1; } else { spin[a][b]=-1; } } } } else { i = distri(gen); j = distri(gen); if (i<lsize-1 && j<lsize-1){ del_E=2*J*(spin[i][j]*(spin[i-1][j] + spin[i+1][j] + spin[i][j-1] + spin[i][j+1])); // periodic boundary condition } else if (i==lsize-1 && j<lsize-1){ del_E=2*J*(spin[i][j]*(spin[i-1][j] + spin[0][j] + spin[i][j-1] + spin[i][j+1])); } else if (i<lsize-1 && j==lsize-1){ del_E=2*J*(spin[i][j]*(spin[i-1][j] + spin[i+1][j] + spin[i][j-1] + spin[i][0])); } else if (i==lsize-1 && j==lsize-1){ del_E=2*J*(spin[i][j]*(spin[i-1][j] + spin[0][j] + spin[i][j-1] + spin[i][0])); } if (exp(-beta*del_E) < 1){ mp_probability = exp(-beta*del_E); } else if (exp(-beta*del_E) >= 1) { mp_probability = 1; } if (dist(gen) < mp_probability){ spin[i][j] = spin[i][j]*(-1); } } for (int a=0;a<lsize;a++){ for (int b=0;b<lsize;b++){ if ((a+1)%2==0 && (a+b)%2==1){ deci[a][b] = spin[a][b]; deci[a][b+1] = spin[a][b]; deci[a-1][b+1] = spin[a][b]; deci[a-1][b] = spin[a][b];//decimation (for block spin) } } } } return 0; }