섀넌은 정보량을 표현하기 위해 다음으로 정보 엔트로피를 정의하였다. 임의의 확률 분포 $X=(p_1, ..., p_n)$에서 계산되는 정보량은

\begin{equation} H(X) \equiv H(p_1, ..., p_n) = -\sum_x p_x \log p_x \end{equation}

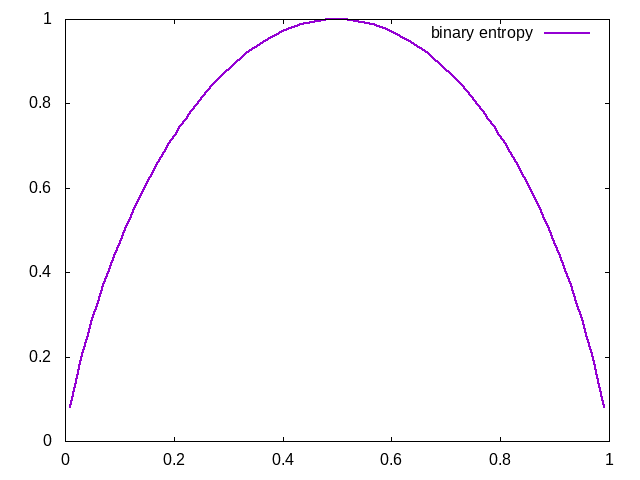
여기서 $\log$는 밑이 2인 로그를 의미한다. $H(p_x)$가 가질수 있는 양의 범위는 $p_x=[0,1]\,, H(p_x)=[0,1]$이며, $p_x=0.5$에서 최댓값을 가지고, 이를 기준으로 대칭인 함수값을 얻는다. 이 때 $p_x=0$인 경우에서 로그의 정의로 인해 $\log0$에 대해 해석하지 못하는 문제가 있지만, 선형함수가 로그보다 더 빠르게 값이 줄기 때문에 $p_x=0$ 이면 $H(X)=0\log0\simeq0$으로 간주한다.

섀넌의 식은 두 가지로 해석할 수 있다.

1. 측정을 한 후 측면에서, “얼마나 많은 정보량을 얻는 가?”
2. 측정을 하기 전 측면에서, “불확정성의 양을 측정”

측정을 하고 나면 결과만을 보고, $H(X)$의 관점에서 생각하면 정보량을 이만큼 얻을 수 있겠다고 생각할 수 있다. 반대로 정보량이 크다는 것은, 어떤 사건이 발생하는 불확실성이 크다는 이야기가 된다.

먼저 보다 간결한, 이항(binary) 정보 엔트로피를 생각한다.

옌센 부등식은 본래 적분의 볼록함수 값과 볼록함수의 적분을 비교하는 부등식이다. 볼록함수 $f$와 지점 $p \in [0,1]$ 에 대해

\begin{equation*} f(px_1-(1-p)x_2) \leq pf(x_1)+(1-p)f(x_2) \end{equation*}

만약 함수 f가 오목함수인 경우, 부등호는 뒤집힌다. 옌센 부등식의 조건을 이용하여, 두 개 이상의 확률 분포를 가지는 엔트로피에 대한 특징을 알 수 있다. 이를테면 동전던지기 예제에서 100원과 500원 동전을 각각 던진다고 생각하자. 동전던지기에 대한 엔트로피는

\begin{equation} H_{\rm flip} = -p\log p -(1-p)\log(1-p) \end{equation}

이고, 100원 동전을 던질 확률 $p_{A}$, 500원 동전을 던질 확률을 $p_{B}$이라고 하고, 이를 결정하는 확률을 q라고 하면,

\begin{equation*} H(qp_{A}+(1-q)p_{B}) \geq qH(p_{A}) + (1-q)H(p_{B}) \end{equation*}

이 때 이항 엔트로피는 오목함수이므로 부등호가 뒤집혔다.

• M.A. Nielsen and I.L. Chuang, Quantum Computation and Quantum Information: 10th Anniversary Edition, Cambridge University Press (2010), Chapter 11