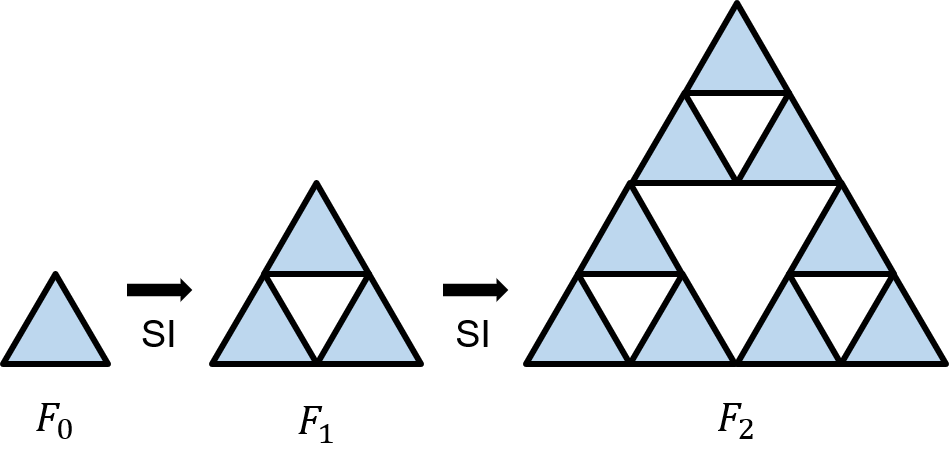프랙탈
프랙탈(fractal)은 일부 작은 조각이 전체와 비슷한 기하학적 형태를 말한다.

프랙탈은 코흐 곡선 (Koch curve)(첫 번째 그림)와 같이 완전히 같은 모양이 반복될 수도 있고(exact), Mandelbrot set(두 번째 그림)과 같이 완전히 같지는 않지만 비슷한 모양이 반복될 수도 있으며(approximate), time series와 같이 확률적으로 프랙탈일 수도 있는(statistical) 등 다양한 종류가 있는 것을 확인할 수 있다.
프랙탈 차원
프랙탈 차원(fractal dimension)은 프랙탈 기하학에서 공간에 패턴을 얼마나 조밀하게 채우는지 나타내는 비율을 말한다.
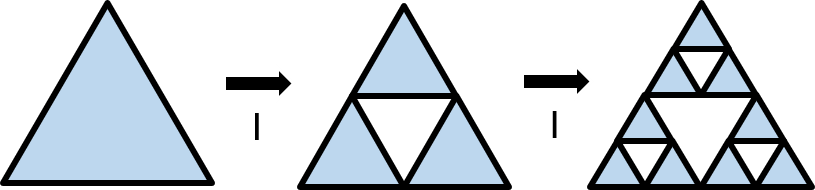
그림은 I 과정을 거칠 때 해상도가 b=2 배율로 반복되는 문양이 나타나게 되고, S 과정을 거칠 때 b=2 배율로 커지는 상황을 나타낸 것이다. 이 때 b를 스케일 팩터(scale factor)라고 한다.
두 과정을 합치게 되면 넓은 공간에서 반복되는 문양이 그려지는 것을 확인할 수 있다. 참고로 위와 같은 도형을 시어핀스키 삼각형(sierpinski triangle)이라고 한다. 이 때 도형의 각 요소에 대해 차원을 표현할 수 있다.
\begin{equation} b^{d_A^{(n)}}\equiv\frac{A((SI)F_n)}{A(F_n)}\\ A(F_n)=\sum_{F_n}O_A \end{equation}
위와 같이 정의되는 식이 있을 때,
\begin{equation} d_A=\lim_{n\rightarrow\infty}d_A^{(n)} \end{equation}
$d_A$를 여기서 프랙탈의 차원이라고 정의한다.
식을 이해하기 위해 예를 통해 알아보자. 위의 시어핀스키 삼각형에서 각 요소에 대해 프랙탈 차원을 구해볼 것이다. 위의 삼각형에서 스케일 팩터 b는 2이다.
첫 번째로 길이에 대한 프랙탈 차원을 구할 것인데, 삼각형 한 변의 길이를 1이라고 하면, SI 과정을 한 번 거치기 전의 삼각형 둘레는 3이고 거친 이후의 둘레는 9이다. 이와 같이 과정을 거칠 때마다 3배씩 늘어나므로 다음과 같이 계산을 할 수 있다.
\begin{equation} 2^{d_L}=3 \rightarrow d_L=ln3/ln2 \end{equation}
두 번째로 삼각형이 채워진 면적에 대해서도 똑같이 3배씩 증가하므로, 같은 방법으로 계산을 할 수 있다.
\begin{equation} 2^{d_A}=3 \rightarrow d_A=ln3/ln2 \end{equation}
세 번째로 조금 더 깊게 들어가서 삼각형이 채워진 이외의 빈 부분의 면적에 대해서도 확인해볼 것이다. 그림에서 맨 왼쪽의 삼각형 하나의 면적을 1이라고 하면, 빈 공간의 넓이는 전체 삼각형의 넓이에서 채워진 삼각형의 넓이를 뺀 값과 같다. 전체 삼각형의 넓이는 $4^n$, 빈 공간의 넓이는 $3^n$으로 계산 가능하므로, 계산하면 다음과 같다.
\begin{equation} 2^{d_V^{(n)}}=\frac{4^{(n+1)}-3^{(n+1)}}{4^n-3^n}=3+\frac{4^n}{4^n-3^n}=3+\frac{1}{1-\left(\frac{3}{4}\right)^n} \\=3+(1+\left(\frac{3}{4}\right)^n+\left(\frac{3}{4}\right)^{2n}+\left(\frac{3}{4}\right)^{3n}+\ldots)\\ =4(1+\frac{1}{4}\left(\frac{3}{4}\right)^n+\frac{1}{4}\left(\frac{3}{4}\right)^{2n}+\ldots) \end{equation}
\begin{equation} d_V=\lim_{n\rightarrow\infty}d_V^{(n)}=\lim_{n\rightarrow\infty}log_2 4(1+\frac{1}{4}\left(\frac{3}{4}\right)^n+\frac{1}{4}\left(\frac{3}{4}\right)^{2n}+\ldots)=2 \end{equation}
이와 같이 같은 도형에서도 각 요소마다 프랙탈 차원은 다르게 나올 수 있다.
차원이 양수일 때 relevant, 음수일 때 irrelevant하다고 하며, 0이거나 실수가 아닌 경우 marginal하다고 할 수 있다. relevant하면 해당 요소가 늘어나는 경우, irrelevant하면 해당 요소가 줄어드는 경우이며 marginal하면 0일 때는 유지되거나, 허수일 경우 주기성을 띤다. 이와 같이 프랙탈 차원을 통하여 SI 과정을 통한 프랙탈 구조에서 각 요소의 상황을 확인할 수 있다.