Table of Contents
모형
2차원 사각 격자 위에서의 이징 모형을 생각하자. 위치를 $x=(n_1,n_2)$로 표기하고 그 점에서의 스핀 값은 $\sigma_x = \pm 1$이다. 상호작용 세기가 $J$이고 외부 자기장이 없다고 하자. 이징 모형의 해밀토니안은 $$E = -J \sum_{\left< xy \right>} \sigma_x \sigma_y$$ 로 주어진다. 이 때에 합은 최근접 이웃에 대해서만 이루어진다는 뜻이다.
온도 $T$에 대해 $\beta \equiv 1/(k_B T)$이면 특정한 스핀 배치 $\left\{ \sigma_x \right\}$가 발견될 확률은 $$P \left( \left\{ \sigma_x \right\} \right) = Z^{-1} \exp\left( K \sum_{\left< xy \right>} \sigma_x \sigma_y \right) $$ 이다. 이 때에 $K \equiv \beta J$로 정의되고 $Z = \sum_{\left\{ \sigma_x \right\}} \exp\left( K \sum_{\left< xy \right>} \sigma_x \sigma_y \right)$는 분배함수이다.
자체 이중성
고온 전개
$K \ll 1$인 상황이다. 다음의 항등식이 유용한데, 이는 $\sigma_x = \pm 1$이기 때문에 성립한다: $$e^{K \sigma_x \sigma_y} = \cosh K (1 + \sigma_x \sigma_y \tanh K).$$ 따라서 스핀 $N$개에 대해 분배함수는 다음과 같다: \begin{eqnarray} Z &=& \sum_{\left\{ \sigma_x \right\}} \prod_{\left< xy \right>} e^{K \sigma_x \sigma_y}\\ &=& \sum_{\left\{ \sigma_x \right\}} \prod_{\left< xy \right>} \cosh K (1 + \sigma_x \sigma_y \tanh K)\\ &=& (\cosh K)^{L} \sum_{\left\{ \sigma_x \right\}} \prod_{\left< xy \right>} (1 + \sigma_x \sigma_y t) \end{eqnarray} 이 때 $L$은 링크의 수이며 $t \equiv \tanh K$로 정의했다. 균일한 사각 격자에서는 $L=2N$일 것이며, 만일 $t=0$이면 $Z = 2^N$이다.
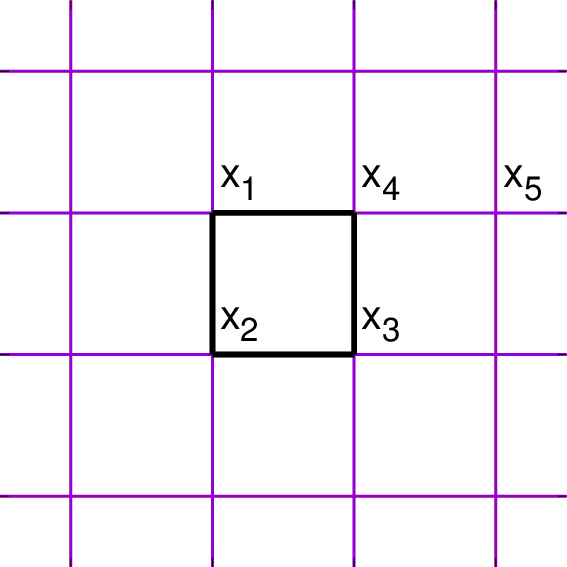
고리의 중요성을 알기 위해 위 그림에 있는 것처럼 4개의 위치($x_1, \ldots x_4$)에 있는 스핀들로 이루어진 고리와, 그 외부에서는 $x_5$에 위치한 스핀만 고려하자 ($N=L=5$). 분배함수는 다음처럼 쓰여질 것이다. \begin{eqnarray} Z/(\cosh K)^{L} &=& \sum_{\left\{ \sigma \right\}} (1+\sigma_1 \sigma_2 t) (1+\sigma_2 \sigma_3 t) (1+\sigma_3 \sigma_4 t) (1+\sigma_4 \sigma_1 t) (1+\sigma_4 \sigma_5 t)\\ &=& \sum_{\left\{ \sigma \right\}} (1+\sigma_1 \sigma_2 t) (1+\sigma_2 \sigma_3 t) (1+\sigma_3 \sigma_4 t) (1+\sigma_4 \sigma_1 t)\\ &&+ \sum_{\left\{ \sigma \right\}} (1+\sigma_1 \sigma_2 t) (1+\sigma_2 \sigma_3 t) (1+\sigma_3 \sigma_4 t) (1+\sigma_4 \sigma_1 t) \sigma_4 \sigma_5 t. \end{eqnarray} 마지막 등식의 두 번째 항이 0이라는 것은 자명하다 ($\sigma_4 \sigma_5 = +1$인 배치가 있으면 반드시 $\sigma_4 \sigma_5 = -1$인 배치가 있어서 상쇄할 것이므로). 따라서 첫 번째 항에서 $\sigma_5 = \pm 1$에 대해 합을 수행하면 다음을 얻는다. $$Z/(\cosh K)^{L} = 2 \sum_{ \sigma_1, \ldots, \sigma_4 } (1+\sigma_1 \sigma_2 t) (1+\sigma_2 \sigma_3 t) (1+\sigma_3 \sigma_4 t) (1+\sigma_4 \sigma_1 t)$$ 즉 고리 안에 들어오지 않는 스핀은 단순히 $2$만큼을 곱해주고 사라진다. 이제 $\sigma_4$, $\sigma_3$, $\ldots$의 순서로 합을 수행할 텐데, $\sigma_x^2=1$임을 이용하면 다음처럼 된다: \begin{eqnarray} Z/(\cosh K)^{L} &=& 2\sum_{ \sigma_1, \ldots, \sigma_4 } (1+\sigma_1 \sigma_2 t) (1+\sigma_2 \sigma_3 t) (1+\sigma_3 \sigma_4 t + \sigma_4 \sigma_1 t + \sigma_1 \sigma_3 t^2)\\ &=& 2^2\sum_{ \sigma_1, \ldots, \sigma_3 } (1+\sigma_1 \sigma_2 t) (1+\sigma_2 \sigma_3 t) (1+\sigma_1 \sigma_3 t^2)\\ &=& 2^4 \sum_{\sigma_1} (1+\sigma_1 \sigma_1 t^4)\\ &=& 2^5 (1+t^4). \end{eqnarray} $t^4$는 사각형의 고리를 의미한다.
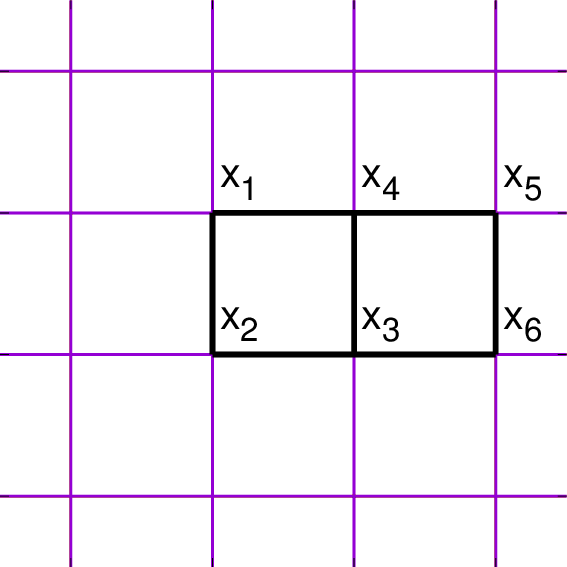
이제 6번째의 스핀을 추가해서 마찬가지 계산을 수행해보면 ($N=6$, $L=7$), $$Z/(\cosh K)^{L} = 2^6 (1+2t^4 + t^6)$$ 으로서, 이는 길이 4인 고리가 2개, 길이 6인 고리가 1개 만들어질 수 있음을 의미한다. 이런 방식으로 분배함수를 $t$의 다항식으로 표현할 수 있으며 그 결과는 계 안에 존재할 수 있는 닫힌 고리들을 셈하는 것과 동등하다.
마지막 예로서 그림에 3개의 스핀을 아래에 덧붙임으로써 $3 \times 3$의 격자를 만들어 계산하면 ($N=9$, $L=12$) $$Z/(\cosh K)^{L} = 2^9 (1+4t^4 + 4t^6+ 7t^8)$$ 을 얻는다. 마지막 항의 계수 7은 스스로를 교차하는 8자 모양의 고리도 포함됨을 말해준다.
저온 전개
분배함수 $$Z = \sum_{\left\{ \sigma_x \right\}} \exp \left( K \sum_{\left< xy \right>} \sigma_x \sigma_y \right)$$ 에서 $g_{xy} \equiv \sigma_x \sigma_y$라고 정의하자. 이 변수는 모든 링크에 존재하므로 $L$개, 균일한 사각 격자라면 $L=2N$개 존재한다. 스핀 변수가 $N$개에 불과하므로 $g_{xy}$들은 서로 독립일 수 없고 일정한 관계를 만족해야만 한다. 구체적으로 말해서, 임의의 닫힌 고리를 따라 계산했을 때 $$\prod_{\text{polygon}} g_{xy} = +1$$ 이어야 한다. 사각 격자에서 사각형 하나를 택해 그 중심의 위치를 $\tilde{x}$라고 칭하자. 그러면 마찬가지로 $$\prod_{\text{around }\tilde{x}} g_{xy} = +1$$ 이어야 한다. 그러니까 위의 분배함수를 $g_{xy}$라는 변수를 가지고 다시 적으려면, 처음엔 마치 $g_{xy}$가 서로 독립인 것처럼 가능성들을 나열한 다음 이 구속조건을 적용해서 실제 스핀으로 구현 가능한 것들만을 추려내야 한다. 수학적으로는, 이 구속조건을 집어 넣어주면 된다: $$\prod_{\tilde{x}} \delta \left(\prod_{\text{around }\tilde{x}} g_{xy} = +1 \right).$$ 그런데 $g_{xy}=\pm 1$이라는 사실로부터 다음 항등식이 가능하다: $$\delta \left(\prod_{\text{around }\tilde{x}} g_{xy} = +1 \right) = \frac{1}{2} \sum_{n=0,1} \left[ \prod_{\text{around }\tilde{x}} g_{xy} \right]^n.$$ 즉 $\prod_{\text{around }\tilde{x}} g_{xy} = +1$이면 우변이 $(1+1)/2=1$이고 반대로 $\prod_{\text{around }\tilde{x}} g_{xy} = -1$이면 우변이 $(1-1)/2=0$이 된다는 뜻이다. $n$도 일반적으로 $\tilde{x}$마다 정의되는 숫자이므로 $n_{\tilde{x}}$라고 부르자. 이제 분배함수를 $g_{xy}$를 가지고 적어보면, \begin{eqnarray} Z &=& \sum_{\left\{ g_{xy} \right\}} \left[ \exp\left( K\sum_{\left< xy \right>} g_{xy} \right) \times \prod_{\tilde{x}} \delta \left(\prod_{\text{around }\tilde{x}} g_{xy} = +1 \right) \right]\\ &=& \sum_{\left\{ g_{xy} \right\}} \left\{ \exp\left( K\sum_{\left< xy \right>} g_{xy} \right) \times \prod_{\tilde{x}} \frac{1}{2} \sum_{n_{\tilde{x}}=0,1} \left[ \prod_{\text{around }\tilde{x}} g_{xy} \right]^{n_{\tilde{x}}} \right\}. \end{eqnarray} 균일한 사각격자라면 사각형의 수는 $N$일 것이므로 그 갯수만큼의 $1/2$을 앞으로 빼주고 다음처럼 적자: \begin{eqnarray} Z &=& \frac{1}{2^N} \sum_{\left\{ g_{xy} \right\}} \left\{ \exp\left( K\sum_{\left< xy \right>} g_{xy} \right) \times \prod_{\tilde{x}} \sum_{n_{\tilde{x}}=0,1} \left[ \prod_{\text{around }\tilde{x}} g_{xy} \right]^{n_{\tilde{x}}} \right\}\\ &=& \frac{1}{2^N} \sum_{\left\{ g_{xy} \right\}} \left\{ \exp\left( K\sum_{\left< xy \right>} g_{xy} \right) \times \sum_{ \left\{ n_{\tilde{x}} \right\}} \prod_{\tilde{x}} \left[ \prod_{\text{around }\tilde{x}} g_{xy} \right]^{n_{\tilde{x}}} \right\}. \end{eqnarray} 마지막 식에 대해 위 6개 스핀의 그림을 예로 들어보자. 왼쪽의 사각형을 $\tilde{x}$, 오른쪽을 $\tilde{y}$라고 부른다면 $$\prod_{\tilde{x}} \sum_{n_{\tilde{x}}=0,1} \left[ \prod_{\text{around }\tilde{x}} g_{xy} \right]^{n_{\tilde{x}}} = \left[ (g_{12}~ g_{23}~ g_{34}~ g_{41})^0 + (g_{12}~ g_{23}~ g_{34}~ g_{41})^1 \right] \times \left[ (g_{43}~ g_{36}~ g_{65}~ g_{54})^0 + (g_{43}~ g_{36}~ g_{65}~ g_{54})^1 \right]$$ 이고 \begin{eqnarray} \sum_{ \left\{ n_{\tilde{x}} \right\}} \prod_{\tilde{x}} \left[ \prod_{\text{around }\tilde{x}} g_{xy} \right]^{n_{\tilde{x}}} &=& (g_{12}~ g_{23}~ g_{34}~ g_{41})^0 (g_{43}~ g_{36}~ g_{65}~ g_{54})^0 +(g_{12}~ g_{23}~ g_{34}~ g_{41})^0 (g_{43}~ g_{36}~ g_{65}~ g_{54})^1\\ &&+(g_{12}~ g_{23}~ g_{34}~ g_{41})^1 (g_{43}~ g_{36}~ g_{65}~ g_{54})^0 +(g_{12}~ g_{23}~ g_{34}~ g_{41})^1 (g_{43}~ g_{36}~ g_{65}~ g_{54})^1 \end{eqnarray} 라는 의미이다.
이제 $Z$를 계산하는데 $\left\{g_{xy}\right\}$에 대한 합과 $\left\{ n_{\tilde{x}}\right\}$에 대한 합의 순서를 바꿀 것이다. 즉 $\left\{ n_{\tilde{x}}\right\}$가 고정된 상태에서 $\left\{g_{xy}\right\}$에 대해 합을 수행한다. 위의 6개 스핀 계에 대해서라면 다음과 같은 류의 계산을 먼저 한 후 가능한 $\left\{ n_{\tilde{x}}\right\}$의 모든 배치에 대해 합한다. \begin{eqnarray} &&\sum_{\left\{ g_{xy} \right\}} \exp \left( K \sum_{\left< xy \right>} g_{xy} \right) \prod_{\tilde{x}} \left[ \prod_{\text{around }\tilde{x}} g_{xy} \right]^{n_{\tilde{x}}}\\ &=&\sum_{\left\{ g_{xy} \right\}} e^{K (g_{12} + g_{23} + g_{34} + g_{41} + g_{36} + g_{65} + g_{54})} (g_{12}~ g_{23}~ g_{34}~ g_{41})^{n_{\tilde{x}}} (g_{43}~ g_{36}~ g_{65}~ g_{54})^{n_{\tilde{y}}}\\ &=& \sum_{\left\{ g_{xy} \right\}} \left( e^{Kg_{12}} g_{12}^{n_{\tilde{x}}} \right) \times \left( e^{Kg_{23}} g_{23}^{n_{\tilde{x}}} \right) \times \left( e^{Kg_{34}} g_{34}^{n_{\tilde{x}}+n_{\tilde{y}}} \right) \times \left( e^{Kg_{41}} g_{41}^{n_{\tilde{x}}} \right) \times \left( e^{Kg_{36}} g_{36}^{n_{\tilde{x}}} \right) \times \left( e^{Kg_{65}} g_{65}^{n_{\tilde{x}}} \right) \times \left( e^{Kg_{54}} g_{54}^{n_{\tilde{x}}} \right). \end{eqnarray} 여기에서 주의해서 봐야 할 부분은 $e^{Kg_{34}} g_{34}^{n_{\tilde{x}}+n_{\tilde{y}}}$로서, 3과 4를 잇는 선과 $\tilde{x}$와 $\tilde{y}$를 잇는 선은 서로를 가로지른다. 지금은 사각형이 2개뿐이고 그들이 만나는 선이 하나뿐이어서 이런 결과를 얻지만 일반적으로는 다음처럼 될 것이다: $$\sum_{\left\{ g_{xy} \right\}} \exp \left( K \sum_{\left< xy \right>} g_{xy} \right) \prod_{\tilde{x}} \left[ \prod_{\text{around }\tilde{x}} g_{xy} \right]^{n_{\tilde{x}}} = \sum_{\left\{ g_{xy} \right\}} \prod_{\left< xy \right>} e^{Kg_{xy}} g_{xy}^{n_{\tilde{x}}+n_{\tilde{y}}}.$$ 이 때에 $xy$와 $\tilde{x} \tilde{y}$는 서로를 가로지른다. 아울러 합과 곱의 순서를 바꾸고 $$\sum_{g_{xy} = \pm 1} e^{Kg_{xy}} g_{xy}^{n_{\tilde{x}}+n_{\tilde{y}}} = e^K + (-1)^{n_{\tilde{x}}+n_{\tilde{y}}} e^{-K}$$ 임을 이용하자. 추가로 무질서 변수 $\mu_{\tilde{x}} = 1-2n_{\tilde{x}} = \pm 1$을 정의하면, 다음처럼 정리된다: \begin{eqnarray} \sum_{\left\{ g_{xy} \right\}} \exp \left( K \sum_{\left< xy \right>} g_{xy} \right) \prod_{\tilde{x}} \left[ \prod_{\text{around }\tilde{x}} g_{xy} \right]^{n_{\tilde{x}}} &=& \prod_{\left< xy \right>} \left[ e^K + (-1)^{1-(\mu_{\tilde{x}}+\mu_{\tilde{y}})/2} e^{-K} \right]\\ &=& \prod_{\left< xy \right>} \left( e^K + \mu_{\tilde{x}} \mu_{\tilde{y}} e^{-K} \right)\\ &=& \prod_{\left< xy \right>} e^K \left( 1 + \mu_{\tilde{x}} \mu_{\tilde{y}} e^{-2K} \right). \end{eqnarray} 따라서 균일한 사각 격자라면 분배함수는 $$Z(K) = \frac{1}{2^N} \sum_{\left\{ \mu_{\tilde{x}} \right\}} \prod_{\left< xy \right>} e^K \left( 1 + \mu_{\tilde{x}} \mu_{\tilde{y}} e^{-2K} \right) = \frac{e^{2NK}}{2^N} \sum_{\left\{ \mu_{\tilde{x}} \right\}} \prod_{\left< xy \right>} \left( 1 + \mu_{\tilde{x}} \mu_{\tilde{y}} e^{-2K} \right)$$ 일 것이다.
스핀 배치 $\{\sigma_x\}$ 하나에 대해 무질서변수의 배치 $\{\mu_{\tilde{x}}\}$가 대응되는 것이 아니다. 오히려 모든 스핀 배치들을 고려했을 때에 무질서변수의 배치 하나가 결정되고 그 역도 성립하는 것이다(Savit, p. 457)
임계점
여기에서 $e^{-2K} = \tanh \tilde{K}$로 정의되는 새로운 결합 상수 $\tilde{K}$를 도입하면 다음처럼 쓸 수 있다: $$(\cosh \tilde{K})^{2N} Z(K) = \frac{e^{2NK}}{2^N} \sum_{\left\{ \mu_{\tilde{x}} \right\}} \prod_{\left< xy \right>} \cosh \tilde{K} \left( 1 + \mu_{\tilde{x}} \mu_{\tilde{y}} \tanh \tilde{K} \right) = \frac{e^{2NK}}{2^N} Z(\tilde{K}).$$ 고온 전개의 서두에 적어놓은 식을 따라서 $Z(\tilde{K})$로 고쳐적었다. 즉 균일한 사각 격자 위에서 $$Z(K) = \left( \frac{1}{\sinh 2\tilde{K}} \right)^N Z(\tilde{K})$$ 로서, 결합상수 $K$인 이징 모형은 결합상수 $\tilde{K}$인 이징 모형과 연결된다. $K$가 높으면 $\tilde{K}$는 낮고 $K$가 낮으면 $\tilde{K}$는 높다. 이징 모형에는 고온과 저온 두 개의 상만이 존재하는데, 고온의 상 하나는 저온의 상 하나와 대응되는 셈이다. $K = \tilde{K}$인 점에서는 $Z(K) = Z(\tilde{K})$로 두 개의 상이 일치하며 여기가 두 상을 나누는 임계점이라고 볼 수 있다. 풀어보면 $K_c = \frac{1}{2} \ln (1+\sqrt{2}) \approx 0.4407$이다.
두 점 사이의 상관함수
앞으로의 편의상 매 링크마다의 결합상수가 다를 수 있다고 가정하고 분배함수를 적어보면 $$Z \left( \left\{ \tilde{K}_{\tilde{x} \tilde{y}} \right\} \right) = \sum_{\left\{\mu_\tilde{x} \right\}} \exp \left( \sum_{\tilde{x} \tilde{y}=nn} \tilde{K}_{\tilde{x} \tilde{y}} \mu_\tilde{x} \mu_\tilde{y} \right)$$ 이다.
인접한 두 점 $\tilde{z}$와 $\tilde{w}$ 사이의 상관함수는 $$ \left< \mu_\tilde{z} \mu_\tilde{w} \right> = Z^{-1} \sum_{\left\{\mu_\tilde{x} \right\}} \mu_\tilde{z} \mu_\tilde{w} \exp \left( \sum_{\tilde{x} \tilde{y}=nn} \tilde{K}_{\tilde{x} \tilde{y}} \mu_\tilde{x} \mu_\tilde{y} \right)$$ 인데, 위의 분배함수를 $\tilde{K}_{\tilde{z}\tilde{w}}$로 미분하면 $$\frac{\partial Z}{\partial \tilde{K}_{\tilde{z}\tilde{w}}} = \sum_{\left\{\mu_\tilde{x} \right\}} \mu_\tilde{z} \mu_\tilde{w} \exp \left( \sum_{\tilde{x} \tilde{y}=nn} \tilde{K}_{\tilde{x} \tilde{y}} \mu_\tilde{x} \mu_\tilde{y} \right) = \left< \mu_\tilde{z} \mu_\tilde{w} \right> Z$$ 임을 알 수 있다. 이중성을 사용해 분배함수를 다시 적어보면 $$Z = \frac{1}{2^N} \sum_{\left\{ \sigma_x \right\}} \prod_{\tilde{x} \tilde{y}=nn} \left( e^{\tilde{K}_{\tilde{x} \tilde{y}}} + \sigma_x \sigma_y e^{-\tilde{K}_{\tilde{x} \tilde{y}}} \right)$$ 이기도 하므로, 다음처럼 적을 수 있다: \begin{eqnarray} \left< \mu_\tilde{z} \mu_\tilde{w} \right> Z &=& \frac{1}{2^N} \sum_{\left\{ \sigma_x \right\}} \left( e^{\tilde{K}_{\tilde{z} \tilde{w}}} - \sigma_z \sigma_w e^{-\tilde{K}_{\tilde{z} \tilde{w}}} \right) \prod_{\tilde{x} \tilde{y} \neq \tilde{z} \tilde{w}} \left( e^{\tilde{K}_{\tilde{x} \tilde{y}}} + \sigma_x \sigma_y e^{-\tilde{K}_{\tilde{x} \tilde{y}}} \right)\\ &=& \frac{1}{2^N} \sum_{\left\{ \sigma_x \right\}} \frac{\left( e^{\tilde{K}_{\tilde{z} \tilde{w}}} - \sigma_z \sigma_w e^{-\tilde{K}_{\tilde{z} \tilde{w}}} \right)}{\left( e^{\tilde{K}_{\tilde{z} \tilde{w}}} + \sigma_z \sigma_w e^{-\tilde{K}_{\tilde{z} \tilde{w}}} \right)} \prod_{\tilde{x} \tilde{y}= nn} \left( e^{\tilde{K}_{\tilde{x} \tilde{y}}} + \sigma_x \sigma_y e^{-\tilde{K}_{\tilde{x} \tilde{y}}} \right)\\ &=& \frac{1}{2^N} \sum_{\left\{ \sigma_x \right\}} \left( \tanh \tilde{K}_{\tilde{z} \tilde{w}} \right)^{\sigma_z \sigma_w} \prod_{\tilde{x} \tilde{y}= nn} \left( e^{\tilde{K}_{\tilde{x} \tilde{y}}} + \sigma_x \sigma_y e^{-\tilde{K}_{\tilde{x} \tilde{y}}} \right)\\ &=& \frac{1}{2^N} \sum_{\left\{ \sigma_x \right\}} \exp \left( -2K_{zw} \sigma_z \sigma_w \right) \prod_{\tilde{x} \tilde{y}= nn} \left( e^{\tilde{K}_{\tilde{x} \tilde{y}}} + \sigma_x \sigma_y e^{-\tilde{K}_{\tilde{x} \tilde{y}}} \right)\\ \end{eqnarray} 따라서 $$\left< \mu_\tilde{z} \mu_\tilde{w} \right> = \left< \exp \left( -2K_{zw} \sigma_z \sigma_w \right) \right>$$ 이며, $zw$와 $\tilde{z} \tilde{w}$는 서로 교차한다.
$\tilde{z}$와 $\tilde{w}$가 인접한 점이 아닐 경우에도 일반화할 수 있다. 예컨대 거리가 2만큼 떨어져 있어서 두 점을 잇는 경로 $\tilde{z} \to \tilde{u}\to \tilde{w}$가 존재한다면 $\mu_\tilde{u}^2 = 1$이라는 사실로부터 $$ \left< \mu_\tilde{z} \mu_\tilde{w} \right> = \left< \mu_\tilde{z} \mu_{\tilde{u}} \mu_{\tilde{u}} \mu_\tilde{w} \right> = Z^{-1} \frac{\partial^2 Z}{\partial \tilde{K}_{\tilde{w}\tilde{u}} \partial \tilde{K}_{\tilde{u}\tilde{z}}}$$ 이기 때문에 위와 같은 계산 과정을 거치면 $$\left< \mu_\tilde{z} \mu_\tilde{w} \right> = \left< \exp \left( -2K_{zw} \sigma_z \sigma_w -2 K_{ab} \sigma_a \sigma_b \right) \right>$$ 임을 확인할 수 있는데, 이 때 $zw$는 $\tilde{z} \tilde{w}$와, $ab$는 $\tilde{u} \tilde{w}$와 교차한다.
즉 경로 $\tilde{\Gamma}_{\tilde{z} \tilde{w}}$로 연결되는 두 점 $\tilde{z}$와 $\tilde{w}$ 사이의 상관함수는 일반적으로 $$\left< \mu_\tilde{z} \mu_\tilde{w} \right> = \left< \exp \left( -2 \sum_{xy \times \tilde{\Gamma}_{\tilde{z} \tilde{w}}} K_{xy} \sigma_x \sigma_y \right) \right>$$ 로서, 합은 이 $\tilde{\Gamma}_{\tilde{z} \tilde{w}}$를 가로지르는 결합선 $xy$들에 대해 이루어진다. 좌변이 두 점 $\tilde{z}$, $\tilde{w}$만의 함수이므로, 이 경로가 구체적으로 어떤 모양인지는 우변의 계산 결과에 영향을 주지 않는다.
$e^{K_{xy}\sigma_x \sigma_y} = \cosh K_{xy} \left(1+\sigma_x \sigma_y e^{-2\tilde{K}_{\tilde{x}\tilde{y}}} \right)$를 이용하여 식을 정리하고 모든 위치에서 상호작용의 크기가 같다고 놓으면 ($K_{xy}=K$, $\tilde{K}_{\tilde{x} \tilde{y}} = \tilde{K}$), 이 식은 다음처럼 두 분배함수의 비에 해당한다: $$\left< \mu_\tilde{z} \mu_\tilde{w} \right> = \frac{\sum_{\{\sigma_z\}} \prod_{xy=nn} e^{K'\sigma_x \sigma_y}}{\sum_{\{\sigma_z\}} \prod_{xy=nn} e^{K\sigma_x \sigma_y}} = \frac{Z'}{Z},$$ 이 때 $K'$은 $xy \times \tilde{\Gamma}_{\tilde{z} \tilde{w}}$에서는 $-K$와 같고 나머지에서는 $K$와 동일하다.
만일 경로 $\tilde{\Gamma}_{\tilde{z} \tilde{w}}$가 닫힌 루프를 이루고 있어서 $\tilde{z} = \tilde{w}$라면 $\left< \mu_\tilde{z} \mu_\tilde{w} \right>=1$로서 $Z' = Z$이다. 이는 경로 $\tilde{\Gamma}_{\tilde{z} \tilde{w}}$의 내부와 외부가 명확히 구분되어 있어서 $Z$에 등장하는 임의의 항을 $Z'$에서도 찾을 수 있음(내부의 스핀을 모두 뒤집으면 된다)을 생각해볼 때에 자명하다.
혼합 상관함수
닫힌 경로가 존재할 때
어떤 닫힌 경로 $\tilde{\Gamma}$가 내부와 외부를 구분하고 있다. $T\left\{ \tilde{\Gamma} \right\} \equiv e^{-\sum_{xy \times \tilde{\Gamma}} 2K_{xy} \sigma_x \sigma_y}$을 생각하자. $Z \equiv \sum_{\{\sigma_z\}} \prod_{xy=nn} e^{K_{xy} \sigma_x \sigma_y}$이고 $Z' = \sum_{\{\sigma_z\}} T\left\{ \tilde{\Gamma} \right\} \prod_{xy=nn} e^{K_{xy} \sigma_x \sigma_y}$라고 정의하면 $\left< T\left\{ \tilde{\Gamma} \right\} \right> = \left< \mu_{\tilde{x} \tilde{x}} \right> = Z'/Z = 1$임을 위에서 보았다. 이제 인접한 스핀 한 쌍을 생각해서 $\left< \sigma_u \sigma_v T\left\{ \tilde{\Gamma} \right\} \right>$를 적어보면 $$ \left< \sigma_u \sigma_v T\left\{ \tilde{\Gamma} \right\} \right> = Z^{-1} \sum_{\{\sigma_z\}} \sigma_u \sigma_v T \prod_{xy=nn} e^{K_{xy} \sigma_x \sigma_y}.$$ $$ \left< \sigma_u \sigma_v T\left\{ \tilde{\Gamma} \right\} \right> = Z^{-1} \sum_{\{\sigma_z\}} \sigma_u \sigma_v T \prod_{xy=nn} e^{K_{xy} \sigma_x \sigma_y} = Z^{-1} \sum_{\{\sigma_z\}} \sigma_u \sigma_v \left( e^{-\sum_{xy \times \tilde{\Gamma}} 2K_{xy} \sigma_x \sigma_y} \right) \prod_{xy=nn} e^{K_{xy} \sigma_x \sigma_y}.$$ 만일 두 스핀이 모두 내부에 있거나 모두 외부에 있어서 둘 사이의 연결선이 $xy\times \tilde{\Gamma}$에 속하지 않는다면 이 양은 간단히 $$\frac{1}{Z} \frac{\partial Z'}{\partial K_{uv}}= \frac{1}{Z} \frac{\partial Z}{\partial K_{uv}} =\left< \sigma_u \sigma_v \right>$$ 이다. 반면 하나는 내부에 다른 하나는 외부에 있어서 둘 사이의 연결선이 $xy\times \tilde{\Gamma}$에 속한다면, $T\left\{ \tilde{\Gamma} \right\}$의 존재로 인해서 $Z'$에 들어가는 $K_{uv}$의 부호가 바뀌게 되고 따라서 $\left< \sigma_u \sigma_v T\left\{ \tilde{\Gamma} \right\} \right>$는 $$-\frac{1}{Z}\frac{\partial Z'}{\partial K_{uv}} = - \frac{1}{Z} \frac{\partial Z}{\partial K_{uv}} =-\left< \sigma_u \sigma_v \right>$$ 이다.
인접하지 않은 임의의 두 스핀을 잡아도 앞에서 논의한 것처럼 두 스핀을 잇는 경로 $\gamma = (u, x_1, x_2, \ldots, x_n, v)$를 설정함으로써 상관함수 $\left<\sigma_u \sigma_v\right> = \left< (\sigma_u \sigma_{x_1}) (\sigma_{x_1} \sigma_{x_2}) (\sigma_{x_2} \sigma_{x_3}) \ldots (\sigma_{x_n}\sigma_{v})\right>$를 계산할 수 있다.
경로 $\gamma$가 $\tilde{\Gamma}$와 교차하는 횟수를 $n_\tilde{\Gamma}$라고 하면 $$\left< \sigma_u \sigma_v T\left\{ \tilde{\Gamma} \right\} \right> = (-1)^{n_\tilde{\Gamma}}\left< \sigma_u \sigma_v \right>$$ 이다.
열린 경로가 존재할 때
$\tilde{z}$와 $\tilde{w}$를 잇는 열린 경로 $\tilde{\Gamma}_{\tilde{z} \tilde{w}}$가 존재하면 마찬가지로 $T\left\{ \tilde{\Gamma}_{\tilde{z} \tilde{w}} \right\} \equiv e^{-\sum_{xy \times \tilde{\Gamma}_{\tilde{z} \tilde{w}}} 2K_{xy} \sigma_x \sigma_y}$ 로 정의할 수 있다. 위와 유사하게 $Z$와 $Z'$을 정의하자. 이때 $\left< \mu_{\tilde{z}} \mu_{\tilde{w}} \right> = \left< T\left\{ \tilde{\Gamma}_{\tilde{z} \tilde{w}} \right\} \right> = Z' / Z$의 관계가 있다.
인접한 스핀 $\sigma_z$와 $\sigma_w$에 대해 $\left< \sigma_z \sigma_w T\left\{ \tilde{\Gamma}_{\tilde{z} \tilde{w}} \right\}\right> = \left< \sigma_z \sigma_w \mu_{\tilde{z}} \mu_{\tilde{w}} \right>$를 계산해보자.
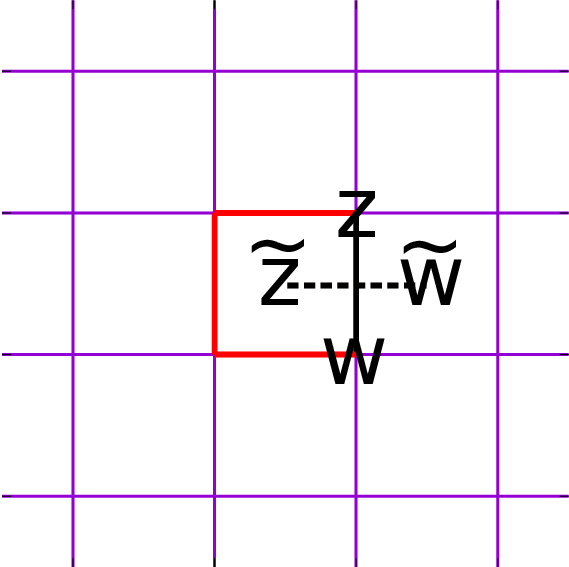
이때 $z$와 $w$를 잇는 선이 $\tilde{\Gamma}_{\tilde{z} \tilde{w}}$를 교차하면 (검은색 수직선) $$\left< \sigma_z \sigma_w \mu_{\tilde{z}} \mu_{\tilde{w}} \right> = -\frac{1}{Z} \frac{\partial Z'}{\partial K_{zw}} = -\left( \frac{Z'}{Z} \right) \left( \frac{\partial Z'/\partial K_{zw}}{Z'} \right) = - \left< \mu_{\tilde{z}} \mu_{\tilde{w}} \right> \left< \sigma_z \sigma_w \right>'$$ 이며 이때 프라임 표시는 $Z'$에 대한 평균임을 의미한다.
하지만 붉은 실선처럼 $\tilde{\Gamma}_{\tilde{z} \tilde{w}}$를 지나지 않고 빙 둘러서 $z$와 $w$를 이을 수도 있다. 그렇다면 마이너스 부호 없이 다음처럼 구해진다. $$\left< \sigma_z \sigma_w \mu_{\tilde{z}} \mu_{\tilde{w}} \right> = \left< \mu_{\tilde{z}} \mu_{\tilde{w}} \right> \left< \sigma_z \sigma_w \right>'.$$
일반적으로 $x$, $y$, $\tilde{z}$, $\tilde{w}$에 대해 혼합 상관함수 $\left< \sigma_z \sigma_w \mu_{\tilde{z}} \mu_{\tilde{w}} \right>$의 값은 $x$와 $y$를 잇는 경로 $\gamma_{xy}$와 $\tilde{z}$와 $\tilde{w}$를 잇는 경로 $\Gamma_{\tilde{z} \tilde{w}}$를 어떻게 선택하느냐에 따라 바뀌는데, 절대값은 바뀌지 않고 두 경로가 교차하는 횟수에 따라 부호가 바뀐다.
자유 페르미온 이론
작용
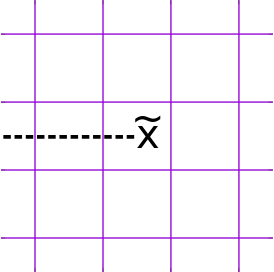
위에서 본 것처럼 평균의 관점에서 $\mu_{\tilde{x}_1} \mu_{\tilde{x}_2} = T\left\{ \Gamma_{\tilde{x}_1 \tilde{x}_2} \right\}$로 간주할 수 있는데 무한히 큰 2차원 격자에서 한쪽 기준점을 마이너스 무한대로 가져다 놓아보자. 임의의 경로 $\Gamma_{\tilde{x}_1 \tilde{x}_2}$는 $\Gamma_{\tilde{x}_1}$과 $\Gamma_{\tilde{x}_2}$를 조합하여 나타낼 수 있다. 그 다음 기준점을 생략하고 임의의 위치 $\tilde{x}$에 대해 $\mu_{\tilde{x}} = T\left\{ \Gamma_{\tilde{x}} \right\}$로 적는다.
어떤 격자점 $x$로부터 이중격자(dual lattice) 상의 인접한 한 점을 가리키기 위해 벡터 $e_a$를 도입하자. 이 때 $e_1$은 북동쪽, $e_2$는 북서쪽, $e_3$는 남서쪽, $e_4$는 남동쪽을 가리키는 벡터이다. 그러면 격자점 주위의 사방을 가리키기 위해 $\Delta_1 \equiv e_1 + e_4 = (1,0)$와 $\Delta_2 \equiv e_1 + e_2 = (0,1)$ 등을 생각할 수 있다. 또 $e_{a+4} = e_a$로서 원래로 돌아오고 $\Delta_{a+2} = -\Delta_a$의 관계식이 존재한다. 이어서 아래와 같은 양을 도입한다: $$\psi_{a,x} = \sigma_x \mu_{x+e_a}.$$
이제 $\mu_{x+e_1} = \mu_{x+e_2} \exp(-2K \sigma_x \sigma_{x+\Delta_2})$ 에 항등식 $\exp(-2K \sigma_x \sigma_{x'}) = \cosh 2K - \sigma_x \sigma_{x'} \sinh 2K$ 을 활용하고 전체에 $\sigma_x$를 곱하면 아래의 식을 얻는다 (단, $\sigma_x^2 = 1$): $$\psi_{1,x} = (\cosh 2K) \psi_{2,x} - (\sinh 2K) \psi_{3,x+\Delta_2}.$$
마찬가지로 $\mu_{x+e_2} = \mu_{x+e_3} \exp(-2K \sigma_{x-\Delta_1} \sigma_x)$ 로부터 $$\psi_{2,x} = (\cosh 2K) \psi_{3,x} - (\sinh 2K) \psi_{4,x-\Delta_1}$$ 을 얻으며, 일반적인 $a$에 대해서는 다음과 같다: $$\psi_{a,x} = (\cosh 2K) \psi_{a+1,x} - (\sinh 2K) \psi_{a+2,x+\Delta_{a+1}}.$$
이때 $\psi_{a+4,x} = -\psi_{a,x}$인데 마이너스 부호는 $a$부터 $a+4$로 한 바퀴를 돌리는 과정에서 점선 경로를 한번 통과하기 때문이다. 또 $\psi_{a,x_1}$과 $\psi_{a,x_2}$ 둘의 위치를 맞바꿀 때에도 점선 경로를 지나게 되기 때문에 마이너스의 부호가 붙는다. 즉 이 변수는 페르미온 같은 성질을 가진다.
임계점에서 $\cosh K = \sqrt{2}$이고 $\sinh K = 1$이어서 $$\psi_{a,x} = \sqrt{2} \psi_{a+1,x} - \psi_{a+2,x+\Delta_{a+1}}$$ 인데 이는 $x$에 무관한 $\psi_a = \omega^a C + \bar{\omega}^a \bar{C}$ 형태의 해를 가진다. 이때 $\omega \equiv e^{i\pi/4}$와 $\bar{\omega} \equiv e^{-i\pi/4}$이고 $C$와 $\bar{C}$는 임의의 상수들이다. 여기에 착안해서 해를 $a$에 의존하는 부분과 $x$에 의존하는 부분으로 나누어 다음의 꼴로 적어보자: $$\psi_a = \frac{\omega^a}{\sqrt{\pi}} \varphi(x) + \frac{\bar{\omega}^a}{\sqrt{\pi}} \bar{\varphi}(x).$$
그 다음 $\varphi(x+\Delta_a) \approx \varphi(x) + \Delta_a \partial_a \varphi(x)$로 근사하면 위의 식들은 다음처럼 정리된다: \begin{eqnarray} (\partial_1 + i\partial_2) \varphi(x) &=& 0\\ (\partial_1 - i\partial_2) \bar{\varphi}(x) &=& 0. \end{eqnarray}
더 일반적으로 임계점 부근에서 $K = K_c + k$이면($k \ll 1$), 근사적으로 $\cosh K \approx \sqrt{2} +2k$이고 $\sinh K \approx 1 + 2\sqrt{2} k$가 되면서 식의 우변이 0이 아니게 된다: \begin{eqnarray} (\partial_1 + i\partial_2) \varphi(x) &=& im \bar{\varphi}(x)\\ (\partial_1 - i\partial_2) \bar{\varphi}(x) &=& -im \varphi(x). \end{eqnarray} 그리고 이때 $m\equiv 4k$로서 그 절대값이 흔히 “질량”이라고 불린다.
$\partial \equiv \frac{1}{2} (\partial_1 - i\partial_2)$와 $\bar{\partial} \equiv \frac{1}{2} (\partial_1 + i\partial_2)$를 정의하면 위의 방정식에 해당하는 작용(action)은 다음과 같은데 $$S = \frac{1}{2\pi} \int d^2 x \left( \varphi \bar{\partial} \varphi + \bar{\varphi} \partial \bar{\varphi} + im \bar{\varphi}\varphi \right),$$ 이를테면 \begin{eqnarray} 0 = \delta_\varphi S &=& \int d^2x \left[ \delta\varphi \bar{\partial} \varphi + \varphi \bar{\partial} (\delta \varphi) + im \bar{\varphi} \delta \varphi \right]\\ &=& \int d^2 x \left[ \delta\varphi \bar{\partial} \varphi + \bar{\partial} (\varphi \delta \varphi) - \bar{\partial} \varphi \delta \varphi + im \bar{\varphi} \delta \varphi \right]\\ &=& \int d^2 x \left[ \delta\varphi \bar{\partial} \varphi + \bar{\partial} (\varphi \delta \varphi) + \delta \varphi \bar{\partial} \varphi + im \bar{\varphi} \delta \varphi \right]\\ &=& \int d^2 x ~\delta \varphi (2\bar{\partial} \varphi - im\bar{\varphi}) \end{eqnarray} 인 것이다. 중간에서 우리는 부분 적분과 페르미온적인 성질 $- \bar{\partial} \varphi \delta \varphi = \delta \varphi \bar{\partial} \varphi$을 사용했다.
반교환자
페르미온적 성질을 가지는 변수들은 그라스만 대수(Grassmann algebra)를 따른다. 예를 들면 반교환(anti-commutator) 연산자를 걸었을 때 $$\int d\varphi d\bar{\varphi} e^{\lambda \bar{\varphi} \varphi} = \int d\varphi d\bar{\varphi} (1+\lambda \bar{\varphi}\varphi) = \lambda$$ 이므로 $$\int d\varphi_1 d\bar{\varphi}_1 \cdots d\varphi_n d\bar{\varphi}_n \exp \left(\sum_\beta \lambda_\beta \bar{\varphi}_\beta \varphi_\beta \right) = \prod_\beta \lambda_\beta$$ 혹은 $$\int D\varphi D\bar{\varphi} \exp \left(-\sum_{\alpha,\beta} \bar{\varphi}_\beta \Lambda_{\beta\alpha} \varphi_\alpha \right) = \det \Lambda.$$ 단, $\Lambda$는 $n \times n$ 행렬이고 여기서 $\bar{\varphi}$ 위의 선이 반드시 복소켤레를 의미할 필요는 없다. 간단한 예로서 $\Lambda = \begin{pmatrix} a & b \\ c & d \end{pmatrix}$이면 \begin{eqnarray} \int d\varphi_1 d\varphi_2 d\bar{\varphi}_1 d\bar{\varphi}_2 \exp \left(-\sum_{\alpha,\beta} \bar{\varphi}_\beta \Lambda_{\beta\alpha} \varphi_\alpha \right) &=& \int d\varphi_1 d\bar{\varphi}_1 d\varphi_2 d\bar{\varphi}_2 \left(\frac{1}{2} \bar{\varphi}_1 a \varphi_1 \bar{\varphi}_2 d \varphi_2 + \frac{1}{2} \bar{\varphi}_2 d \varphi_2 \bar{\varphi}_1 a \varphi_1 + \frac{1}{2} \bar{\varphi}_1 b \varphi_2 \bar{\varphi}_2 c \varphi_1 + \frac{1}{2} \bar{\varphi}_2 c \varphi_1 \bar{\varphi}_1 b \varphi_2 \right) \\ &=& ad-bc. \end{eqnarray}
이제 $n$이 짝수일 때 $n \times n$의 반대칭 행렬 $\Lambda$에 대해($\Lambda_{\alpha\beta} = -\Lambda_{\beta\alpha}$) $\bar{\varphi}$에 대한 적분 없이 쓰면 다음의 적분을 행하면 행렬식(determinant) 대신 그 반쪽에 해당하는 파피안(Pfaffian)을 얻는다: $$\int D\varphi \exp \left(-\frac{1}{2} \sum_{\alpha,\beta} \varphi_\beta \Lambda_{\beta\alpha} \varphi_\alpha \right) = \text{Pfaff} (\Lambda).$$ 이때 $[\text{Pfaff}(\Lambda)]^2 = \det \Lambda$이다. 예를 들어 두 개의 독립적인 그라스만 변수 $\varphi_1$과 $\varphi_2$가 있을 때 $\Lambda = \begin{pmatrix} 0 & a \\ -a & 0 \end{pmatrix}$이라면 $$\int d\varphi_1 d\varphi_2 \exp \left(-\frac{1}{2} \sum_{ij} \varphi_i \Lambda_{ij} \varphi_j \right) = \int d\varphi_1 d\varphi_2 \exp \left(-\frac{1}{2} \varphi_1 a \varphi_2 + \frac{1}{2} \varphi_2 a \varphi_1 \right) = \int d\varphi_1 d\varphi_2 \left( 1-\frac{1}{2} \varphi_1 a \varphi_2 + \frac{1}{2} \varphi_2 a \varphi_1 \right) = a.$$
행렬이 블록으로 쪼개어질 때 $\det \Lambda = \prod_i \det \Lambda_i$로 쓸 수 있는 것처럼 $\text{Pfaff} \Lambda = \prod_i \text{Pfaff} \Lambda_i$처럼도 쓸 수 있다.
자유에너지
다시 작용을 적어보면 $$S = \frac{1}{2\pi} \int d^2 x (\varphi \bar{\partial} \varphi + \bar{\varphi} \partial \bar{\varphi} + im\bar{\varphi} \varphi)$$ 이며, 여기에서 미분연산자는 반대칭행렬로 나타낼 수 있음에 유의할 것. 예를 들어 간격 $\Delta$로 $N$개의 입자가 늘어서 있는 길이 $L=N\Delta$의 1차원 계를 생각한다면 \begin{eqnarray} &&\int dx \left( \frac{1}{2}\varphi \partial_1 \varphi + \frac{1}{2}\bar{\varphi} \partial_1 \bar{\varphi} + im\bar{\varphi} \varphi \right) \approx \sum_{j=0}^{N-1} \frac{1}{2} \varphi_j \left( \frac{\varphi_{j+1} - \varphi_{j-1}}{2\Delta} \right) + \frac{1}{2} \bar{\varphi}_j \left( \frac{\bar{\varphi}_{j+1} - \bar{\varphi}_{j-1}}{2\Delta} \right) + im \bar{\varphi}_j \varphi_j\\ &=& \begin{pmatrix} \varphi_0 & \varphi_1 & \cdots & \varphi_{N-1} & \bar{\varphi}_0 & \bar{\varphi}_1 & \cdots & \bar{\varphi}_{N-1} \end{pmatrix} \left( \begin{array}{cccccc|cccccc} 0 & \frac{1}{4\Delta} & 0 & \cdots & 0 & -\frac{1}{4\Delta} & -\frac{im}{2} & 0 & 0 & 0 & \cdots & 0\\ -\frac{1}{4\Delta} & 0 & \frac{1}{4\Delta} & \cdots & 0 & 0 & 0 & -\frac{im}{2} & 0 & 0 & \cdots & 0\\ \vdots & & & \ddots & & & \vdots & & & & \ddots & \vdots \\ \frac{1}{4\Delta} & 0 & 0 & \cdots & -\frac{1}{4\Delta} & 0 & 0 & 0 & 0 & 0 & \cdots & -\frac{im}{2}\\\hline \frac{im}{2} & 0 & 0 & 0 & \cdots & 0 & 0 & \frac{1}{4\Delta} & 0 & \cdots & 0 & -\frac{1}{4\Delta}\\ 0 & \frac{im}{2} & 0 & 0 & \cdots & 0 & -\frac{1}{4\Delta} & 0 & \frac{1}{4\Delta} & \cdots & 0 & 0\\ \vdots & & & \ddots & & \vdots & \vdots & & & & \ddots & \vdots \\ 0 & 0 & 0 & 0 & \cdots & -\frac{im}{2} & \frac{1}{4\Delta} & 0 & 0 & \cdots & -\frac{1}{4\Delta} & 0 \end{array}\right) \begin{pmatrix} \varphi_0 \\ \varphi_1 \\ \vdots \\ \varphi_{N-1} \\ \bar{\varphi}_0 \\ \bar{\varphi}_1 \\ \vdots \\ \bar{\varphi}_{N-1} \end{pmatrix}\\ &=& -\frac{1}{2} \sum_{\alpha=0}^{2N-1} \sum_{\beta=0}^{2N-1} \tilde{\varphi}_\alpha \Lambda_{\alpha\beta} \tilde{\varphi}_\beta. \end{eqnarray} 여기에서는 중심미분을 사용했지만 앞에서와 일관되게 $\partial_1 \varphi \approx (\varphi_{j+1}-\varphi_j)/\Delta$를 사용해도 마찬가지이다. 편의상 주기적 경계조건을 가정했다.
이것을 지수함수 위에 올려 적분하는 분배함수는 $$Z = \int D\tilde{\varphi} \exp(-S) = \text{Pfaff}\Lambda = \prod_{n=0}^{N-1} \left( \frac{1}{\Delta^2} \sin^2 k_n \Delta + m^2 \right)^{1/2} \xrightarrow[\Delta \to 0]{} \prod_{n=0}^{N-1} \left( k_n^2 + m^2 \right)^{1/2}$$
2차원 문제로 돌아와서 $k^2=k_x^2 +k_y^2$으로 일반화하고 $Z$에 로그를 취하면 \begin{eqnarray} -\beta f &=& \frac{1}{L^2} \ln Z \propto \frac{1}{2} \int \frac{d^2 k}{(2\pi)^2} \ln (k^2 + m^2) = \frac{1}{8\pi^2} \int dk ~2\pi k \ln (k^2 + m^2)\\ &=& \frac{1}{8\pi} [(k^2+m^2) \ln(k^2+m^2) - k^2] = \frac{1}{8\pi} m^2 \ln(m^2) + k^2 \ln(m^2) + O(k^4). \end{eqnarray} 장파장 영역($k \to 0$)에서 $-\beta f \propto m^2 \ln m^2$이며 $m = 4(K-K_c)$이므로 $m$으로의 미분은 $K$로의 미분과 대응된다. 즉 $\frac{\partial^2 f}{\partial K^2} \propto -\ln m^2$이 되어 비열이 임계점에서 로그 발산을 보인다.
함께 보기
참고문헌
- Robert Savit, Duality in field theory and statistical systems, Rev. Mod. Phys. 52, 453 (1980).
- Ising Field Theory by A. Zamolodchikov, https://www.weizmann.ac.il/complex/falkovich/courses
- V. N. Plechko, J. Phys. Studies, 1, 554 (1997).
- J.M Carmona, A. Di Giacomoa, and B. Lucini, A disorder analysis of the Ising model, Phys. Lett. B, 485, 126 (2000).
- Massimo D’Elia and Luca Tagliacozzo, Direct numerical computation of disorder parameters, Phys. Rev. D 74, 114510 (2006).