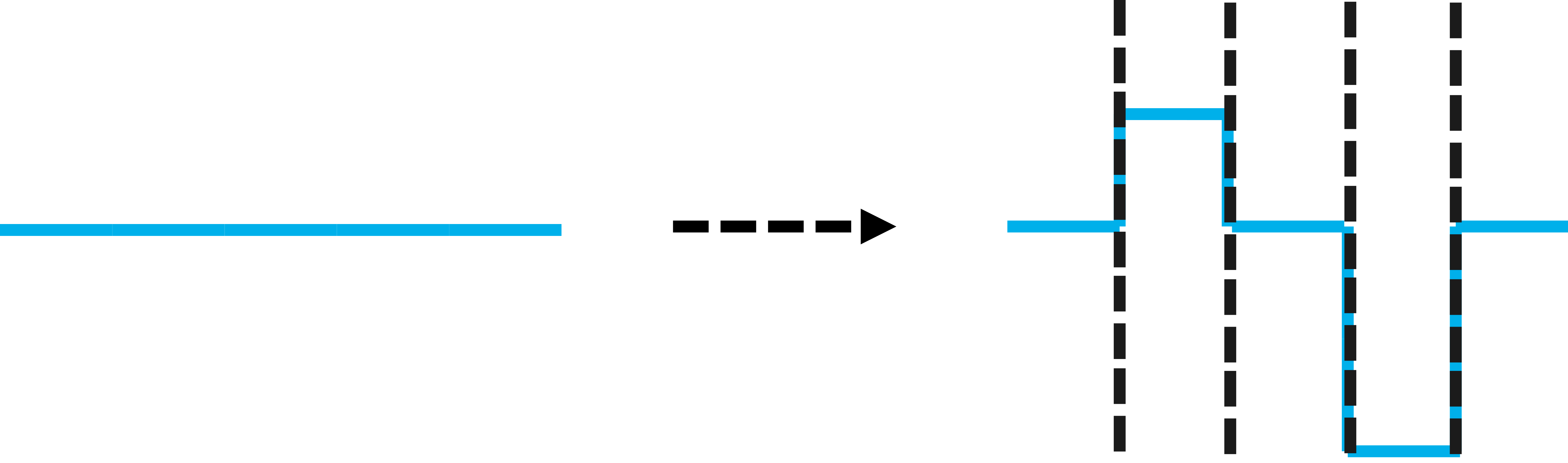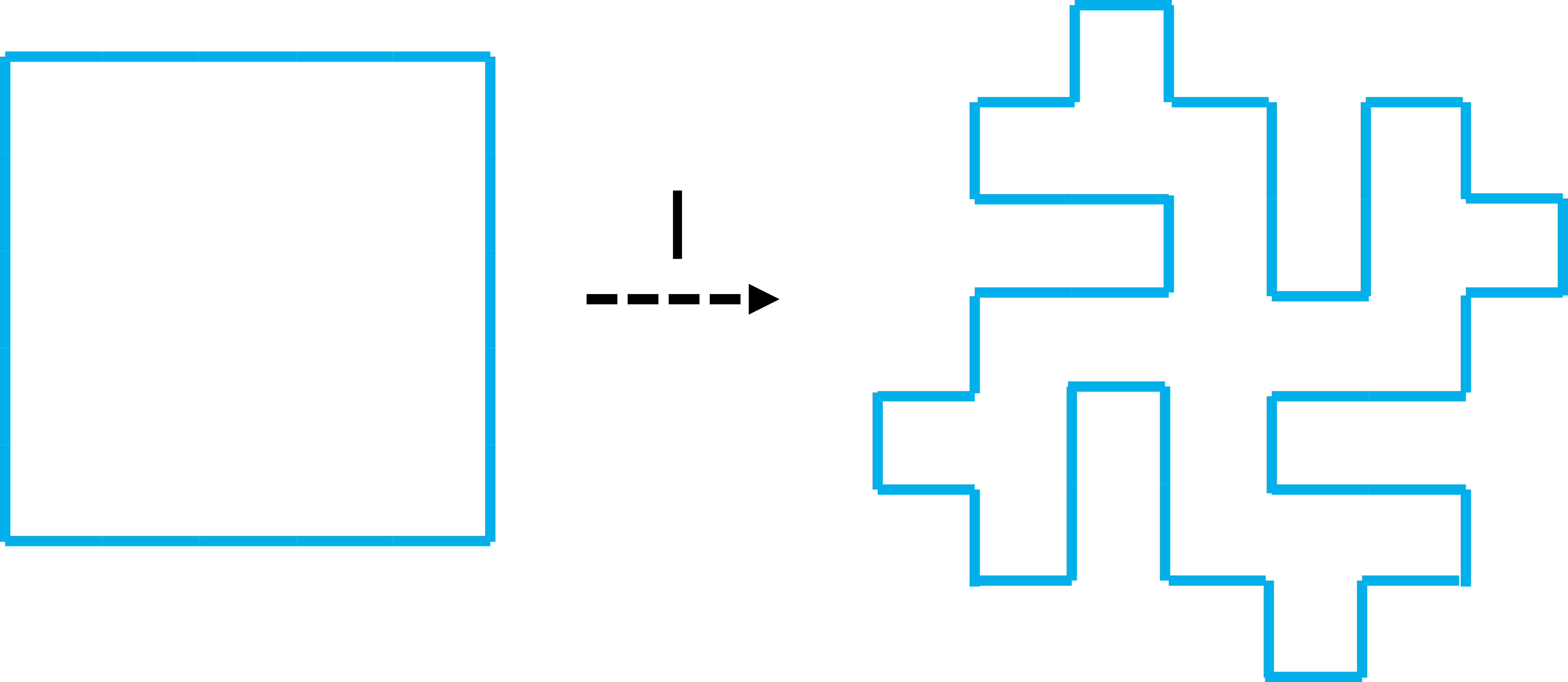코흐 곡선은 여러 프랙탈 도형중의 하나로, 같은 모양이 지속적으로 반복되는 프랙탈이다. 다양한 도형을 생각해볼 수 있으며, 여기서는 아래와 같은 모양을 형성하는 선을 예시로 살펴보자.

위의 그림에서, 길이 5인 직선이 변환 I를 거침으로, 선의 총 길이가 11로 변한것을 알 수 있다. 우측의 수직점선을 그은 것과 같이, 선의 모양변화를 5구역으로 나누어 생각해볼 수 있다. 이러한 변환을 만드는 도형은 스케일 팩터가 $b=5$이고, 따라서 프랙탈의 길이 차원 $d_L$은

\begin{equation} 5^{d_L} = 11 \, \rightarrow \, d_L = \ln11 / \ln5 \end{equation}

으로 결정된다. 프랙탈의 차원에 대한 자세한 설명은 프랙탈 차원을 참고할 수 있다.

이제 여기서 크기를 키우는 작업을 시행하자. 그 변환을 S라고 부르고, 크기는 5배씩 증가시킨다. 과정 S와 I는 도형의 변환에 따라 그 수가 달라지는 데, 지금의 경우에서는 선 하나에 대해서 5개 구역으로 나뉠 수 있으므로, 변환 1회시 S와 I가 각 5배가 된다. 초기 도형에서 변환 I, S, I를 거치면 아래와 같은 도형이 된다.

(※ 하나의 이미지에 담기 위해 여기서는 변환 S를 2.5배로 두었다.)

이번에는 하나의 선을 이용하여 형성된 프랙탈을 면으로 구성하여 변환을 거쳐보자. 이러한 프랙탈 도형을 이차 코흐곡선(Quadratic Koch curve), 이차 코흐 섬(Quadratic Koch island), 또는 코흐 눈꽃송이(Koch snowflake) 등으로 불린다. 앞의 과정과 같이 선의 길이는 5이고, 여기서는 기본 도형이 사각형으로 시작하여 각 선분마다 변환을 시행한다.

마찬가지로 다음 변환을 진행하기 위해, 가로 및 세로의 길이를 5배 늘리고, 변환 I를 진행하여 그림을 그릴 수 있을 것이다. 하지만 앞의 선의 경우와 달리 면을 형성하고 있어 다소 복잡하므로, 다음 변환을 생각하기 위해 규칙을 찾아보자. 사각형이 변환 I를 거쳐 모습이 형성되었을 때, 2차원 격자를 그어 살펴보자.

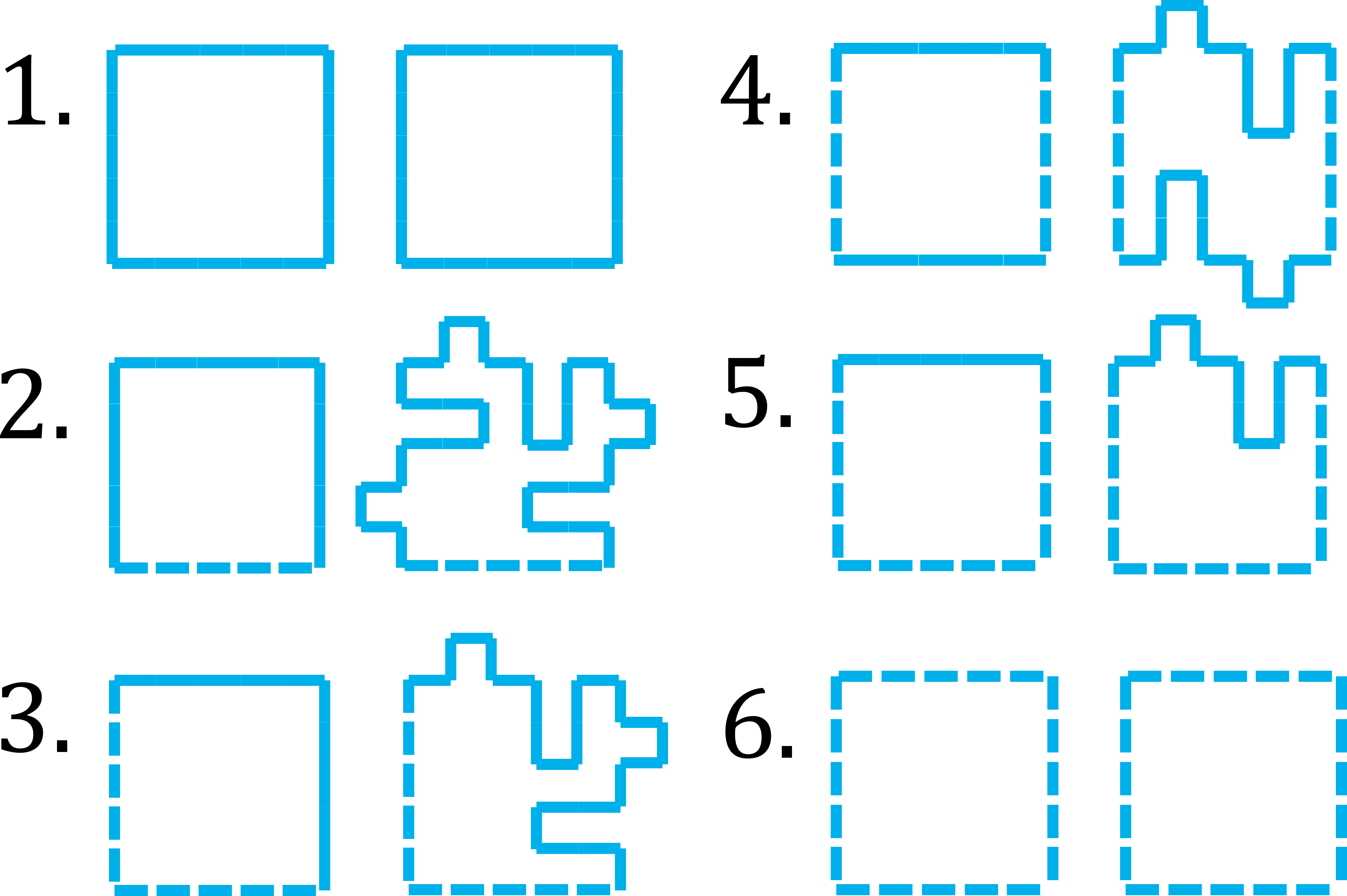
외부는 신경쓰지 않고, 내부에서 형성되는 사각형을 살펴보면, 6가지의 공통된 사각형을 가지는 것을 확인할 수 있다.

번호순대로 모양별 사각형을 square, dead-end, corner, parallel, line, empty라고 부르자. 오른쪽에 그려진 도형은 각 도형별로 변환 I를 거쳤을 때 생각할 수 있는 그림이다.

주어진 변환을 행렬로 구성하고, 변환되는 사각형을 벡터로 구성하면, 간단히 선형방정식으로 구성할 수 있는 것을 알 수 있다. 각 사각형에 대한 기저를 아래와 같이 구성하자.

\begin{equation} \mathbf{d} = \left( d_{\rm sq}\,, d_{\rm dead}\,, d_{\rm cor}\,, d_{\rm para}\,, d_{\rm line}\,, d_{\rm empty} \right) \end{equation}

위 식의 기저를 순서로 하여, 도형 변환 I와 크기 변환 S의 행렬 SI를 아래와 같이 구성할 수 있을 것이다.

\begin{align} SI = \begin{pmatrix} 0 & 0 & 0 & 0 & 0 & 0 \\ 8 & 5 & 3 & 2 & 1 & 0 \\ 4 & 4 & 3 & 4 & 2 & 0 \\ 4 & 2 & 1 & 0 & 0 & 0 \\ 4 & 6 & 5 & 8 & 4 & 0 \\ 1 & 5 & 11 & 9 & 17 & 25 \end{pmatrix} \end{align}

따라서 n-1번의 변환을 거친 프랙탈에 대해 아래와 같은 선형 방정식을 세울 수 있다.

\begin{equation} \mathbf{d}_{n} = SI \mathbf{d}_{n-1} = SI^{n-1} \mathbf{d}_1 \qquad (n \geq 2) \end{equation}

하지만 이는 편의상 우리가 살펴보는 직교좌표계의 행렬이므로, 고유방정식을 계산하여 실제 프랙탈 구성요소의 직교좌표로 구성된 공간의 모습을 살펴보자. 행렬 SI를 대각화하면

\begin{align} D= \begin{pmatrix} 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 0 & 11 & 0 \\ 0 & 0 & 0 & 0 & 0 & 25 \end{pmatrix} \end{align}

$\lambda_{\rm sq}\,, \lambda_{\rm dead}\,, \lambda_{\rm cor}$는 0, $\lambda_{\rm para}$는 1, $\lambda_{\rm line}$는 11, $\lambda_{\rm empty}$는 25의 고윳값을 가지는 것을 확인할 수 있다. 코흐 곡선의 정의에서 길이 차원을 구한 것과 같이, 면적에 대한 차원을 계산해 볼 수 있는데,

\begin{align*} 5^{{d}_{\rm{sq}}} =& 5^{{d}_{\rm{dead}}} = 5^{{d}_{\rm{cor}}} = 0 \\ 5^{{d}_{\rm{para}}} =& 1 \, \rightarrow \, d_{\rm{para}} = \ln 1 / \ln 5 = 0 \\ 5^{d}_{\rm{line}} =& 11 \, \rightarrow \, d_{\rm{para}} = \ln 11 / \ln 5 \\ 5^{d}_{\rm{empty}} =& 25 \, \rightarrow \, d_{\rm{para}} = \ln 25 / \ln 5 = 2 \\ \end{align*}

따라서 $d_{\rm sq}\,, d_{\rm dead}\,, d_{\rm cor}$는 irrelevant하며, $d_{\rm para}$는 marginal, $d_{\rm line}$와 $d_{\rm empty}$는 relevant하다.

한편 각 고유값에 대응되는 고유벡터는, \begin{equation*} \begin{aligned} \mathbf{d}_{\rm{sq}} =& \, \left( -1 ~~ 4 ~~ -4 ~~ 0 ~~ 0 ~~ 1 \right) \\ \mathbf{d}_{\rm{dead}} =& \, \left( 0 ~~ 1 ~~ -2 ~~ 0 ~~ 1 ~~ 0 \right) \\ \mathbf{d}_{\rm{cor}} =& \, \left( 1 ~~ -2 ~~ 0 ~~ 1 ~~ 0 ~~ 0 \right) \end{aligned} \qquad \begin{aligned} \mathbf{d}_{\rm{para}} =& \, \left( 0 ~~ 1 ~~ -1 ~~ 1 ~~ -3 ~~ 2 \right) \\ \mathbf{d}_{\rm{line}} =& \, \left( 0 ~~ -98 ~~ -112 ~~ -28 ~~ -196 ~~ 379 \right) \\ \mathbf{d}_{\rm{empty}} =& \, \left( 0 ~~ 0 ~~ 0 ~~ 0 ~~ 0 ~~ 1 \right) \end{aligned} \end{equation*}

고유벡터로 구성되는 행렬 Q를 $Q = \left( \mathbf{d}_{\rm{sq}}\,, \mathbf{d}_{\rm{dead}}\,, \mathbf{d}_{\rm{cor}}\,, \mathbf{d}_{\rm{para}}\,, \mathbf{d}_{\rm{line}}\,, \mathbf{d}_{\rm{empty}} \right)$ 으로 구성하면, 간단히 대각행렬 D만 계산하여 n번의 변환을 거친 프랙탈 기본 구성 사각형의 총 개수를 얻을 수 있다. \begin{equation*} SI^{n} = \left( QDQ^{-1} \right)^{n} = QD^{n}Q^{-1} \end{equation*}

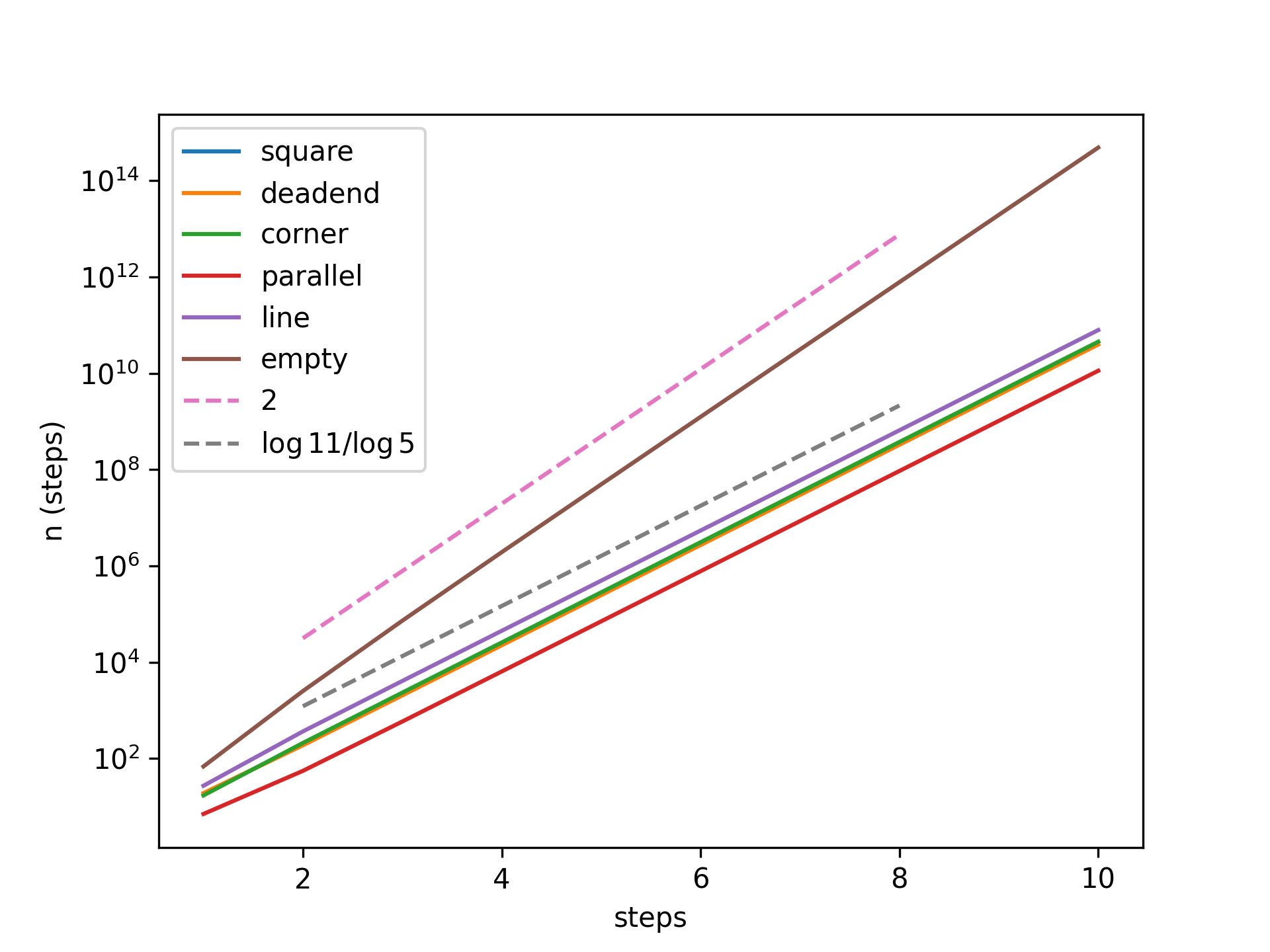
위 식의 성질을 이용하여 python의 numpy, matplotlib를 이용한 코드는 아래와 같다.

| fractalstep.py

import numpy as np
import numpy.linalg as lin
import matplotlib.pyplot as plt
 
matrix = np.array(
        [[0,0,0,0,0,0],
        [8,5,3,2,1,0],
        [4,4,3,4,2,0],
        [4,2,1,0,0,0],
        [4,6,5,8,4,0],
        [1,5,11,9,17,25]]
)
 
steps = 10
eigval, eigvec = lin.eig(matrix)
diagmat = np.zeros((6,6))
np.fill_diagonal(diagmat,eigval)
diagmat0 = diagmat
sum_mat = np.zeros((6,steps))
for i in range(steps):
        A = eigvec @ diagmat @ lin.inv(eigvec)
        for j in range(6):
                sum_mat[j][i] = np.sum(A[j])
        diagmat = diagmat0 @ diagmat
 
x = np.arange(1,steps+1,1)
label = ['square', 'deadend', 'corner', 'parallel', 'line', 'empty']
for i in range(6):
        plt.plot(x, sum_mat[i], label=label[i])
plt.yscale('log')
plt.plot((2,8),(5**5*10,5**17*10),'--',label='2')
log_5_11=np.log(11)/np.log(5)
plt.plot((2,8),(5**(log_5_11*2)*10,5**(log_5_11*8)*10),'--',label=r'$\log 11 / \log 5$')
plt.xlabel('steps')
plt.ylabel('n (steps)')
plt.legend()
plt.savefig('kochgraph.png', dpi=300, transparent=True)

• 프랙탈 차원
• The 19th KIAS-APCTP Winter School on Statistical Physics