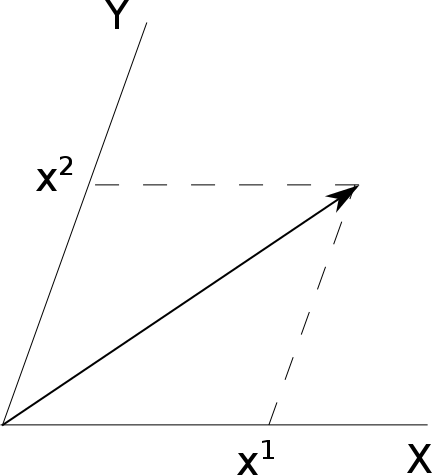
좌표계의 축들이 직교하지 않는다고 해보자. 이 때 벡터를 성분으로 나타내려면 두 가지 방안이 있을 수 있다.

하나는 왼쪽처럼 축에 평행한 방향으로 선을 그어서 표현하는 방법이다. 이렇게 표현하는 벡터를 $\vec{r} = x^1 \vec{a}_1 + x^2 \vec{a}_2$라고 하자. $\vec{a}_i$는 적절한 기저 벡터이고, 윗 첨자는 제곱을 의미하는 것이 아님에 주의한다.

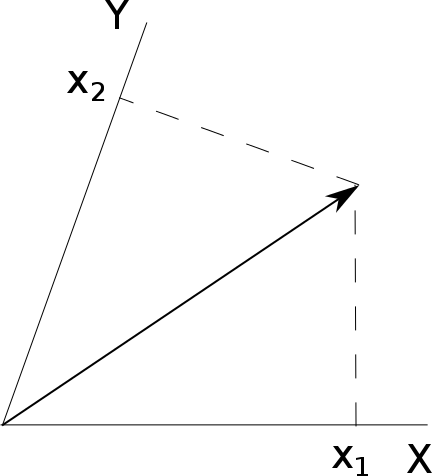
다른 방법은 오른쪽 그림처럼 축에 수선을 내림으로써 표현하는 것이다. 이렇게 표현하는 벡터를 $\vec{r} = x_1 \vec{a}^1 + x_2 \vec{a}^2$으로 적자. 마찬가지로 $\vec{a}^i$는 적절한 기저 벡터로, $\vec{a}_i$와 일반적으로 같지 않다.

좌표축이 수직하다면 이 두 표기법을 구분할 필요는 없다.

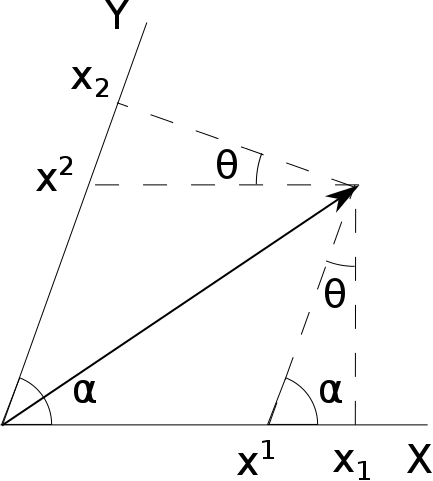
아인슈타인 표기법에 따르면 $\vec{r} = x_i \vec{a}^i = x^i \vec{a}_i$이며, 반면 $\vec{r} \neq x_i \vec{a}_i$이고 $\vec{r} \neq x^i \vec{a}^i$이다. 이제 이 둘을 같이 그려보자.

좌표축 사이의 각도를 $\alpha$라고 하자. 벡터의 화살표 끄트머리로부터 $x^1$으로 내려오는 선과 $x_1$으로 내려오는 선 사이의 각도를 $\theta$라고 하면, 위 그림 오른쪽의 삼각형으로부터 $\alpha+\theta = \pi/2$임을 쉽게 알 수 있다.

그 삼각형을 좀더 들여다보면, 밑변의 길이가 $x_1 - x^1$이고 가장 긴 변의 길이는 $x^2$이다. 둘 사이의 각도가 $\theta$이므로 다음의 식을 얻는다: $$ x_1 - x^1 = x^2 \sin \theta. $$ 마찬가지로 제일 위에 놓인 삼각형을 보면 $$ x_2 - x^2 = x^1 \sin \theta. $$ 임을 알게 된다. 다시 말해서, $$\begin{pmatrix} x_1 \\ x_2 \end{pmatrix} = \begin{pmatrix} 1 & \sin\theta\\ \sin\theta & 1 \end{pmatrix} \begin{pmatrix} x^1\\ x^2 \end{pmatrix} $$ 이라는 것이다. 중간의 $2 \times 2$ 행렬을 $g$라고 부르면 다음처럼 적을 수 있다: $$x_i = g_{ij} x^j.$$

위 그림에서 벡터의 길이 $r^2$은 코사인 법칙에 의해 $$r^2 = x^1 \times x^1 + x^2 \times x^2 - 2x^1 x^2 \cos(\pi - \alpha)$$ 이다. 위에서 $\alpha+\theta = \pi/2$임을 보였으므로 $\cos (\pi-\alpha) = -\cos\alpha = -\sin \theta$이고 따라서 $$r^2 = x^1 \times x^1 + x^2 \times x^2 + 2x^1 x^2 \sin\theta = \begin{pmatrix} x^1 & x^2 \end{pmatrix} \begin{pmatrix} 1 & \sin\theta\\ \sin\theta & 1 \end{pmatrix} \begin{pmatrix} x^1\\ x^2 \end{pmatrix} $$ 이다. 위에서 정의한 $g$가 다시 등장하였으므로 $$r^2 = x^i g_{ij} x^j = x^i x_i$$ 라고 줄여 쓸 수 있다.

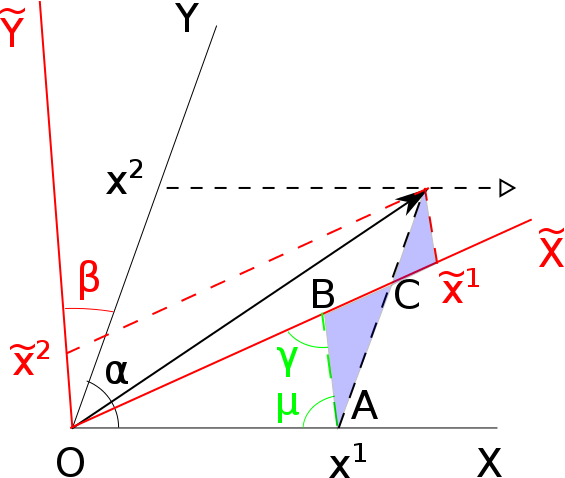
위의 좌표축을 각도 $\beta$만큼 회전시켜보자. 아래 그림처럼 벡터 $\vec{r}$은 이 새로운 좌표축 $(\tilde{X}, \tilde{Y})$에서 $\tilde{x}^1$과 $\tilde{x}^2$라는 성분으로 기술될 것이다.

설명의 편의를 위해, $O\tilde{Y}$에 평행하게 $A=x^1 \vec{a}_1$으로부터 $\tilde{X}$ 축 위로 선분을 긋자. 이 때에 만들어지는 각을 $\gamma$와 $\mu$라고 부르고 있다. 위 그림에서 이 두 각을 포함하고 있는 삼각형 OAB를 보면, 그 둘을 제외한 나머지 각 BOA는 단순히 회전각 $\beta$이므로 $\beta + \gamma + \mu = \pi$임을 알 수 있다.

삼각형 OAB에서 붉은 색으로 칠해진 변 OB의 길이는 사인 법칙에 의해 $x^1 \frac{\sin \mu}{\sin \gamma}$이다.

그 옆의 색칠된 삼각형 두 개는 서로 닮음인데, 그 중 큰 쪽을 보면, 아래에 놓인 예각 BAC는 $\beta$와 같고 왼쪽 위의 둔각 ABC는 $\pi - \gamma$와 같다. 따라서 사인 법칙을 다시 한번 이용하면, 이 삼각형에서 붉은 색 실선으로 나타낸 변 BC의 길이는 검은 점선으로 나타낸 변 AC의 $\frac{\sin \beta}{\sin \gamma}$ 배일 것이다

작은 삼각형도 닮음에 의해 마찬가지. 그리고 두 삼각형에서 검은 점선 두 개 길이의 합은 $x^2$에 다름 아니므로 결과적으로 우리는 $\tilde{x}^1$의 크기를 알게 되었다: $$\tilde{x}^1 = x^1 \frac{\sin\mu}{\sin\gamma} + x^2 \frac{\sin\beta}{\sin\gamma}.$$

다른 한편, $x_2$를 고정한 채 $x_1$을 늘려갈 때 $\tilde{x}_1$이 얼마나 변화하는지 생각해보자. 즉 위 그림에서 빈 화살표 방향으로 진행하는 것을 의미한다. 여기에서도 사인 법칙을 이용하면 그 변화량이 $$ \left( \frac{\partial \tilde{x}^1}{\partial x^1} \right)_{x^2} = \frac{\sin\mu}{\sin\gamma}$$ 임을 보일 수 있다.

또 이번에는 $x_1$를 고정한 채 $x_2$을 늘려갈 때 $\tilde{x}_1$이 얼마나 변화하는지를 생각해본다면, 이는 선분 AC를 연장시키며 진행하는 것에 대응하는데, 그 변화량은 다음과 같다: $$ \left( \frac{\partial \tilde{x}^1}{\partial x^2} \right)_{x^1} = \frac{\sin\beta}{\sin\gamma}.$$

다시 말해서, $$\tilde{x}^1 = \left( \frac{\partial \tilde{x}^1}{\partial x^1} \right)_{x^2} x^1 + \left( \frac{\partial \tilde{x}^1}{\partial x^2} \right)_{x^1} x^2$$ 이 성립하고 더 일반적인 표현식으로는 $$ \tilde{x}^j = \frac{\partial \tilde{x}^j}{\partial x^k} x^k $$ 이 된다.

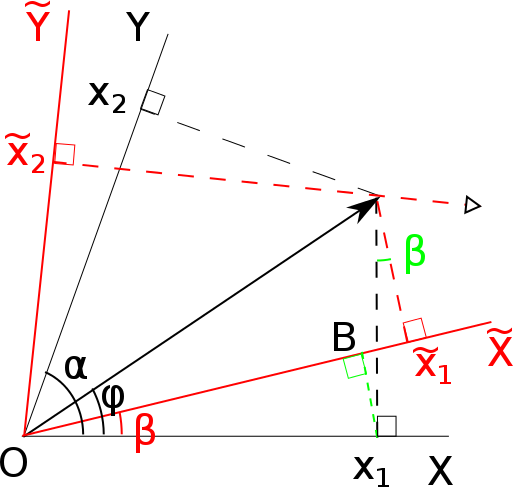
이번에는 축에 수선을 내린 경우에서 좌표축을 각도 $\beta$만큼 회전해보자.

$\tilde{x}_1$의 표현식을 구하려고 한다.

먼저 선분 OB의 길이는 $x_1 \cos\beta$임을 $X$ 축과 비교함으로써 알 수 있다.

나머지 부분의 길이를 구하기 위해, 벡터의 화살표 끝에서 $X$ 축으로 내린 검은색 점선을 보자. 여기에 $\sin\beta$를 곱하면 우리가 알고자 하는 길이가 된다.

그리고 벡터 $\vec{r}$의 길이를 $r$이라 하면 그 검은색 점선의 길이는 $r \sin\phi$이다.

요컨대, $\tilde{x}_1 = x_1 \cos\beta + r \sin\phi \sin\beta$이다.

그런데 벡터의 길이 $r$에 대해 다음 식이 성립함을 쉽게 알 수 있다. $$ r = \frac{x_1}{\cos\phi} = \frac{x_2}{\cos(\alpha-\phi)}. $$ 이를 통해 $r$을 소거하고 다음처럼 쓸 수 있다.

$$\tilde{x}_1 = x_1 \frac{\sin(\alpha-\beta)}{\sin\alpha} + x_2 \frac{\sin\beta}{\sin\alpha}.$$

그런데 $\tilde{x}_2$를 고정한 채 $\tilde{x}_1$을 증가시켰을 때 $x_1$이 얼마나 변화하는지를 보면 (빈 화살표 참조) $$ \left( \frac{\partial x_1}{\partial \tilde{x}_1} \right)_{\tilde{x}_2} = \frac{\sin(\alpha-\beta)}{\sin\alpha}$$ 임을 보일 수 있다.

마찬가지로 $\tilde{x}_2$를 고정한 채 $\tilde{x}_1$을 증가시켰을 때 $x_2$가 얼마나 변화하는지를 보면 $$ \left( \frac{\partial x_2}{\partial \tilde{x}_1} \right)_{\tilde{x}_2} = \frac{\sin\beta}{\sin\alpha}$$ 이다. 따라서 $$\tilde{x}_1 = \left( \frac{\partial x_1}{\partial \tilde{x}_1} \right)_{\tilde{x}_2} x_1 + \left( \frac{\partial x_2}{\partial \tilde{x}_1} \right)_{\tilde{x}_2} x_2$$ 이고 더 일반적으로 적으면 다음과 같다: $$\tilde{x}_j = \frac{\partial x_k}{\partial \tilde{x}_j} x_k.$$

위의 그림을 다시 한번 생각해보자. 사인 법칙에 의해 $$\frac{r}{\sin(\pi-\alpha)} = \frac{x^1}{\sin(\alpha-\phi)} = \frac{x^2}{\sin\phi}$$ 이므로 $$x^1 = r \frac{\sin(\alpha-\phi)}{\sin\alpha},$$ $$x^2 = r \frac{\sin\phi}{\sin\alpha}$$ 임을 알 수 있다.

다른 한편, 공변 성분은 간단히 $x_1 = r \cos\phi$, $x_2 = r \cos(\alpha-\phi)$이다.

위의 표현식들을 이용해 $\phi_1$ 방향을 가리키는 반변 벡터 $\vec{F}$와 $\phi_2$ 방향을 가리키는 공변 벡터 $\vec{s}$를 내적해보자: $$F^i s_i = F^1 s_1 + F^2 s_2 = F \frac{\sin(\alpha-\phi_1)}{\sin\alpha} s \cos\phi_2 + F \frac{\sin\phi_1}{\sin\alpha} s \cos(\alpha-\phi_2).$$ 이 때에 $F \equiv |\vec{F}|$, $s \equiv |\vec{s}|$이다. 코사인과 사인을 전개하고 정리하면 $$F^i s_i = F s \cos(\phi_1 - \phi_2)$$ 로서 올바른 결과를 얻는다.

텐서 분석에서는 어떤 물리적 실재가 있다는 것, 그래서 우리가 관찰을 위해 선택한 특정한 좌표계와 무관하게 동일한 것으로 남아있어야 한다는 생각이 바탕에 깔려 있다. 이를 위해 공변과 반변이 같이 등장해야 한다.위키피디아의 탁월한 비유처럼, 만일 우리가 좌표의 축척을 100만큼 나누어서 미터 대신 센티미터로 길이를 재고자 한다면 좌표축에 등장하는 숫자는 100배를 곱해줘야 한다 (즉 1m = 100cm). 전자가 공변이라면 후자는 반변이다. 벡터의 경우에도 공변과 반변이 같이 있음으로써 이러한 불변성이 보장된다: $$\vec{v} = v_i \vec{a}^i = v^i \vec{a}_i.$$ 기울기(gradient) 벡터가 공변이라고 하는 것은 그 원소가 공변이라는 뜻이다: $$\left( \nabla u \right)_i = \frac{\partial u}{\partial x^i} = \frac{\partial \tilde{x}^j}{\partial x^i} \frac{\partial u}{\partial \tilde{x}^j}.$$ 기울기 벡터 자체를 적어보면 $$\nabla u = \frac{\partial u}{\partial x^i} \vec{a}^i$$ 로서, 여기에서 만일 $u = x^j$라면 $$\nabla u = \frac{\partial x^j}{\partial x^i} \vec{a}^i = \delta^j_i \vec{a}^i = \vec{a}^j$$ 가 됨으로써 기울기는 반변 벡터가 될 수 있다. 이는 그 원소가 공변이라는 진술과 모순이 아니라 오히려 잘 들어맞는 결과이다.

$x^i$ 좌표계에서 아주 짧은 변위 벡터는 $d\vec{s} = dx^i \vec{a}_i$ 이고 따라서 그 제곱은 $ds^2 = dx^i dx^j \vec{a}_i \cdot \vec{a}_j$이다. $g_{ij} \equiv \vec{a}_i \cdot \vec{a}_j$로 정의하면 $ds^2 = g_{ij} dx^i dx^j$이며, 이 때 $g_{ij}$를 계량 텐서라고 부른다.

데카르트 좌표계에서 $g_{ij} = \delta_{ij}$이다.

이제 기저 벡터 $\vec{\alpha}_i$를 가지는 새로운 $\tilde{x}^i$ 좌표계를 생각해보자. 변위 벡터가 $\vec{s} = \tilde{x}^i \vec{\alpha}_i = \tilde{x}_i \vec{\alpha}^i$로 표현되므로 $$\vec{\alpha}_j = \frac{\partial}{\partial \tilde{x}^j} \vec{s} = \frac{\partial x^i}{\partial \tilde{x}^j} \vec{a}_i$$ 이다. 기존 좌표계에서의 기저 벡터 $\vec{a}_i$로 표현되었음에 유의한다. 행렬 $J$가 원소로서 $$J_{ij} = \frac{\partial x^i}{\partial \tilde{x}^j}$$ 를 가진다고 하자. 위 $\vec{\alpha}_j$의 표현식과 비교해보면, $J$의 $j$ 번째 열은 $\vec{\alpha}_j$를 기존 좌표계에서 표현한 것에 해당한다. 그리고 새로운 좌표계에서의 공변 계량 텐서는 행렬 $\tilde{g} = J^T J$로 표현된다.

원래의 $x^i$ 좌표계에서의 기술을 이 $\tilde{x}^i$ 좌표계로 옮겨주는 행렬 $R$을 고려하면, 그 행렬의 원소는 다음처럼 주어진다: $$R_{ij} = \frac{\partial \tilde{x}^i}{\partial x^j}.$$ 한편 우리는 이미 $\nabla x^i = \vec{a}^i$임을 보았다. 이는 $\nabla \tilde{x}^i = \vec{\alpha}^i$임을 유츄하게끔 해주는데, 이 때 $\nabla$는 원래의 $x^i$ 좌표계에서 계산하는 것임에 유의하라. 즉 새로운 좌표계 $\tilde{x}_i$가 가지는 기저 벡터 $\vec{\alpha}^i$들을 기존 좌표계에서 표현하는 것이다. 그러한 방식으로 이 $R$의 $i$ 번째 행은 $\vec{\alpha}^i$를 나타낸다.

$R = J^{-1}$이므로 $J^T J R R^T = I$임은 자명하다. 이를 고쳐 적어보면 $R J = J^T J R R^T = \tilde{g} R R^T$ 인데 좌변의 $R J$는 새로운 좌표계에서 적은 $\vec{\alpha}_j$들을 묶어놓은 것이고, 제일 오른쪽에 등장하는 $R R^T$는 마찬가지로 새로운 좌표계에서 적은 $\vec{\alpha}^i$들을 열 벡터들로 묶어둔 것이다. 이 좌표계에서 적은 계량 텐서 $\tilde{g}$가 양쪽을 연결해주는데, 구체적으로는 반변 텐서를 공변으로 바꾸어준다.

예를 들어 $\left\{ \begin{array}{lcl} x_1&=&\tilde{x}_1+\tilde{x}_2
x_2&=&\tilde{x}_2 \end{array}\right.$, 혹은 다른 말로 $\left\{ \begin{array}{lcl} \tilde{x}_1&=&x_1-x_2
\tilde{x}_2&=&x_2 \end{array}\right.$, 라고 해보자. 위의 $J$ 행렬은 이 경우 다음처럼 구해질 것이다: $$J = \begin{pmatrix} 1 & 1\\0 & 1 \end{pmatrix} = \begin{pmatrix} \vec{\alpha}_1 & \vec{\alpha}_2. \end{pmatrix}$$ 따라서 계량 텐서는 $\tilde{g} = J^T J = \begin{pmatrix} 1 & 1\\1 & 2 \end{pmatrix} = \begin{pmatrix} g_{11} & g_{12} \\ g_{21} & g_{22} \end{pmatrix}$이다. 다른 한편으로 위에서 쓴 $R$ 행렬은 아래와 같을 것이다: $$R = \begin{pmatrix} 1 & -1 \\ 0 & 1 \end{pmatrix} = \begin{pmatrix} \vec{\alpha}^{1^T} \\ \vec{\alpha}^{2^T} \end{pmatrix}.$$ 위의 항등식 $RB = gRR^T$로부터 아래의 관계식을 쉽게 확인할 수 있다: $$R \begin{pmatrix} \vec{\alpha}_1 & \vec{\alpha}_2 \end{pmatrix} = g R \begin{pmatrix} \vec{\alpha}^1 & \vec{\alpha}^2 \end{pmatrix}.$$ 즉 새로운 좌표계에서 기술한 반변 텐서 $R \vec{\alpha}^i$가 $\tilde{g}$에 의해 (역시 새로운 좌표계에서 기술한) 공변 텐서 $R \vec{\alpha}_i$로 옮겨진다.

• http://nct.goetheanum.org/cocontra.htm
• http://mathpages.com/rr/s5-02/5-02.htm
• http://www.openicon.com/mu/math/gradient_covariance/gradient_covariance.html