난수를 이용한 함수의 적분법이다.

다음과 같은 적분을 계산한다고 생각해보자.

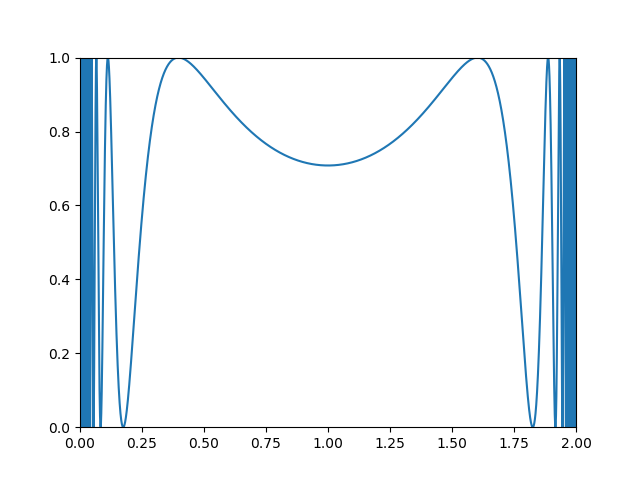
$$ I = \int_0^2\sin^2\left[\frac{1}{x(2-x)}\right]dx $$

적분할 함수의 개형을 보면 양 끝 점으로 갈수록 무한히 가파르게 변하는 모습을 볼 수 있다. 반면, 함수의 그래프가 2$\times$1인 사각형 안에 알맞게 들어오기 때문에 적분값이 유한하고 그 값이 2보다 작다는 것을 알 수 있다. 수치적분을 할 때 사다리꼴 적분법이나 가우스 구적법을 많이 사용하지만 이러한 방법들은 위와 같이 가파르게 변하는 함수의 적분값을 적절하게 구해주지 못한다. 이러한 경우에 다른 여러 방법들 중에서 많이 사용하는 방법 중 하나가 몬테 카를로 적분법이다.

함수를 적분한다는 것은 기하학적으로 그 함수의 그래프가 가지는 면적을 구한다는 것과 같다. 이러한 원리를 이용하기 위해서 2$\times$1이란 제한된 면적 위에 임의로 점을 찍는다고 생각해보자. 그 점들 중에서 함수값보다 작은 $y$ 값을 갖는 점이 있을 것이고 우리는 이러한 점의 갯수가 우리가 찍은 전체 점의 갯수 중에서 가지는 비율을 구할 수 있다. 이러한 과정을 많이 반복하다 보면 이 비율이 곧 제한된 공간 안에서 그래프가 가지는 면적의 비율과 비슷한 값을 가질 것이라 생각할 수 있다. 즉 이와 같은 $N$ 번의 시행 중에서 함수값보다 작은 $y$ 값을 갖는 점의 갯수가 $k$ 개, 제한된 공간의 전체 넓이 $A$에서 함수가 그리는 그래프의 넓이를 $I$라 하면

$$ \frac{I}{A} \sim \frac{k}{N}$$

의 관계를 얻을 수 있다. 이 관계식을 정리하여 다시 쓰면 다음과 같이 적잘한 적분값을 구할 수 있다.

$$ I \sim \frac{kA}{N} $$

무작위로 뽑은 점 하나가 함수값 보다 작을 확률이 $ p = I/A $이므로 함수값 보다 크거나 같은 값을 가질 확률은 $ 1-p $이다. 만약 무작위 수를 뽑는 횟수가 $N$ 번이고 이 중 함수값보다 작은 값을 가지는 수가 $k$개가 뽑일 확률은

$$ P(k) = \binom{N}{k}p^k(1-p)^{N-k} $$

이 되어 이항분포를 가진다. 이항분포의 분산 식을 이용하면

$$\text{var}~k = Np(1-p) = N\frac{I}{A}\left(1-\frac{I}{A}\right) $$

임을 알 수 있다. 그러므로 표준편차를 아래와 같이 얻을 수 있다.

$$ \sigma_N = \sqrt{\text{var}~k}\frac{A}{N} = \frac{\sqrt{I(A-I)}}{\sqrt{N}} $$

따라서 무작위 수를 $N$ 번 얻어 몬테 카를로 적분법을 사용하면 난수를 이용하여 구한 적분의 기댓값과 비교하여 $1/\sqrt{N}$에 비례하는 오차를 가지는 것을 알 수 있다.

$$ \sigma_N \sim \frac{1}{\sqrt{N}} $$

평균값 방법

1. M. E. J. Newman, Computational Physics (Createspace Independent Pub, 2012).