울프 군집 셈법(Wolff cluster algorithm) 혹은 울프 셈법(Wolff algorithm)은 이징 모형(Ising model)에서 온도 $T$가 $T\neq0$일 때, T에 따라 스핀을 뒤집는 셈법으로 군집 셈법(cluster algorithm) 중 하나이다.
온도 $T$가 주어져 있고 외부 자기장이 없는 경우에 상호작용 세기를 $J=1$, 볼츠만 상수 $k_B = 1$로 가정하면 울프 군집 셈법은 다음과 같은 순서로 작동한다. 일반적인 경우 뒤집히는 확률은 $1-exp(-2\beta J)$다.
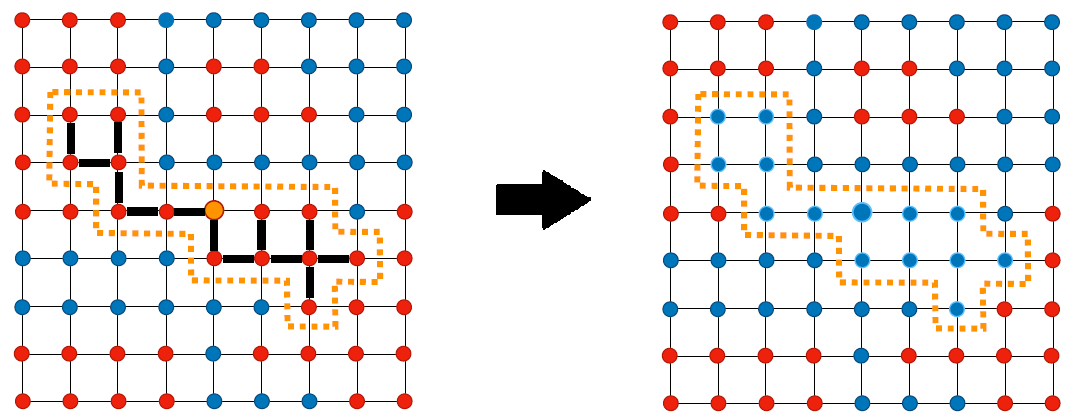
- 먼저 입자 하나를 무작위로 고른다.
- 그 입자의 최근접 이웃 입자 중 같은 스핀을 가진 입자들을 모두 찾고, 찾아진 이웃들에 대해서 더이상 같은 스핀을 가진 최근접 이웃이 없을 때까지 계속하여 찾는다.
- 1번에서 선택된 입자의 스핀을 뒤집고, 2번에서 찾은 입자들의 스핀을 $1-exp(-2/T)$의 확률로 뒤집는다.
- 1번으로 돌아가서 2~3번을 반복한다.
결과적으로 아래와 같은 그림처럼 한 스텝에 입자들이 군집을 이뤄서 뒤집히게 된다.
다음은 울프 셈법으로 주기적 경계(periodic boundary)를 갖는 128$\times$128 크기의 정사각 격자(square latice)에서 단계(step)별 자화(magnetization)를 구하고 파일로 내보내는 C++코드이다. 초기 상태는 모두가 한 방향으로 정렬되어 있는 상태다.
- | wolff.cpp
#include <fstream> #include <cmath> #include <vector> #include <deque> #include <random> using std::vector; using std::deque; using std::ofstream; using std::random_device; using std::uniform_real_distribution; using std::uniform_int_distribution; using std::mt19937_64; using std::exp; using std::abs; using std::pow; random_device rd; mt19937_64 rng(rd()); uniform_real_distribution<double> dds(0,1); void Wolff(int N, int k, vector<int> &S, vector<vector<int>> A, double p, double &m); int main() { int N = 128;//lattice length double T = 4.0;//given temparature double p = 1.0-exp(-2.0/T);//flip probability double m = 1.0; //magnetization int mcs_max = (int)(pow(2,20)+0.5); //max montecarlo step int eq_time = 100000; //equilibrium time vector<int> S(N*N, 1);//spin information array vector<vector<int>> A(N*N, vector<int>(4,-1));//the closest neighbor information for(int i = 0; i < N; ++i) { for(int j = 0; j < N; ++j) { A[i*N + j][0] = i*N + (j+1)%N; //the right particle A[i*N + j][1] = i*N + (j-1+N)%N; //the left particle A[i*N + j][2] = ((i+1)%N)*N + j; //the above particle A[i*N + j][3] = ((i-1+N)%N)*N + j; //the below particle } } ofstream fout; fout.open("mag.dat"); //output file //equlibrium step for(int i = 0; i < eq_time; ++i) { int loc = ids(rng); Wolff(N, loc, S, A, p, m); } uniform_int_distribution<int> ids(0,(N*N)-1); //measure the magnetization for(int i = 0; i < mcs_max; ++i) { int loc = ids(rng); Wolff(N, loc, S, A, p, m); fout << i << "," << m << "\n"; } fout.close(); } void Wolff(int N, int k, vector<int> &S, vector<vector<int>> A, double p, double &m) { int nc = 1; //# of cluster int s0 = S[k]; //the spin information of selected particle int ind = -1; //the particle index S[k] = -s0; // flip spin deque<int> dq; //queue for saving same spin neighbor index dq.emplace_back(k); //save selected particle's index dq.shrink_to_fit(); //free memories which are not used while(!dq.empty()) { ind = dq.front(); //extract information of the leftmost queue dq.pop_front(); //remove the leftmost queue for(int j = 0; j < A[ind].capacity(); ++j) { if(S[A[ind][j]] == s0) //compare the spins { if(dds(rng) < p) //proceed in the probability p { dq.emplace_back(A[ind][j]);//save the neigbor's index dq.shrink_to_fit();//free memories S[A[ind][j]] = -s0;//flip spin ++nc; //add 1 to # of cluster } } } } m = 0.0; //calculating the magnetization for(int i = 0; i < S.capacity(); ++i) { m += (double)S[i]/(N*N); } m = abs(m); }