개요
입실론 기계(epsilon machine)은 시계열의 패턴을 찾기 위해 개발된 방법이다. 주어진 과거들에 대해 앞으로 나올 기호의 확률 분포를 보고 통계적으로 충분히 비슷할 경우 묶어서 하나의 '상태'로 간주한다는 것이 핵심 아이디어이다. '상태'들과 그 상태들 간의 전이확률은 시계열로부터 추출되며, 이런 전이의 모형들 중 정보 관점에서 가장 단순한 모형을 선택한다.
알고리듬
입실론 기계를 만들기 위한 대표적인 방법은 원인 상태 분할 구축 (Causual State Splitting Reconstruction, CSSR) 알고리듬이다. 여기에서는 시계열을 만들어내는 확률과정을 최대한 단순한 것으로 가정한 다음 단순한 가정이 설명하지 못하는 통계를 만나면 새로운 상태를 추가해 나간다. 물론 설명 여부는 적절한 통계적 기법을 통해 판정되어야 한다.
짝수 과정(Even process)의 실행 예
이 예는 참고문헌 항목의 첫 번째인 Shalizi 등의 논문에서 가져온 것이며, 입실론 기계 구축의 세부적인 설명은 두 번째 참고문헌인 Cirera의 학위논문에서 가져온 것이다.
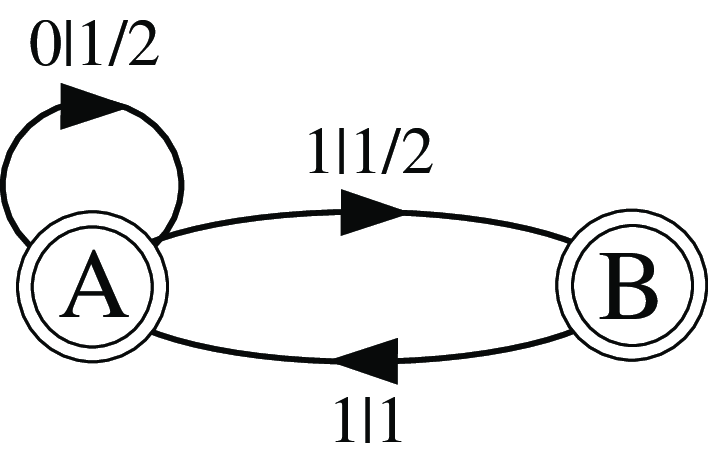
짝수 과정은 다음처럼 구성된다. 먼저 0,1로 이루어진 시계열 뒤에는 두 개의 숨은 상태 A, B가 존재한다. A는 1/2의 확률로 0을 내놓고 머무르거나 1을 내고 B로 전이한다. 반면 B는 언제나 1을 내고 A로 전이한다. 그 결과 1의 연쇄는 짝수번만 가능하고, 010, 01110, 0111110, … 처럼 홀수 번 나오는 것은 불가능하다. 그림으로 나타내면 아래와 같다 (Shalizi et al.):
짝수 과정이 특히 흥미로운 것은, 우리가 A와 B라는 숨은 상태를 찾지 않고 0과 1의 시계열 자체만을 본다면 절대로 마르코프 연쇄로 표현할 수 없는 과정이라는 점이다. 이는 1의 연쇄가 아무리 길게 이어져도 짝수와 홀수를 구분한다는 점에서 기억의 길이가 사실상 무한대이기 때문에 그러하다.
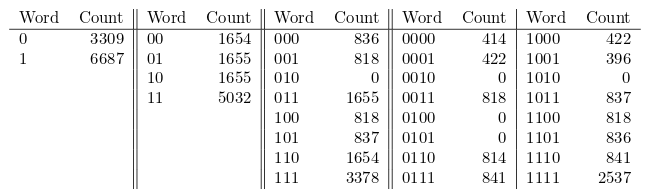
이 짝수 과정을 통해 길이가 $10^4$인 시계열을 얻었고, 이로부터 다음과 같은 통계를 뽑아내었다고 하자(Shalizi et al.):
우리는 길이가 $L_\text{max}=3$인 문자열 후에 등장하는 문자까지만 보려고 한다. 그렇기 때문에 위의 표는 길이 4인 문자열의 빈도까지 기록하고 있다. 이것이 짝수 과정을 올바로 재구축하기 위한 최소한의 길이이다.
$L=0$의 통계
CSSR 알고리듬은 가장 간단한 가정에서부터 시작한다. 즉 아무런 기억 없이 일정한 확률로 0과 1이 나온다고 가정하는 것이다. 아무 기억이 없다는 뜻에서 $\emptyset$을 써놓고, 계의 상태가 이것 하나만 존재하므로 그 이름을 $A=\{ \emptyset \}$으로 놓자. 표의 가장 왼쪽을 보면, 상태 $A$에 있을 때 1이 따라나올 확률은 66.9%이다.
$L=1$의 통계
이제 직전에 나온 기호에 의존한다고 가정해보자. 표에서 왼쪽으로부터 두 번째 칸, 그러니까 00, 01 등의 빈도를 보여주는 영역을 보아야 한다.
- 0이 나왔을 때 다음에 1이 나올 확률은 1655/3309 = 50.0%이다. 이는 상태 $A$로부터 예측되는 것과는 다르다. 따라서 $B=\{0\}$이라는 상태를 새로 만들어야 한다.
- 1이 나왔을 때에 1이 따라나올 확률은 5032/6687=75.3%로서, 역시 $A$와는 다르고 $B$와도 다르다. 따라서 $C=\{1\}$을 새로운 상태로 추가한다.
$A=\{\emptyset\}$으로부터 파생된 위의 두 경우가 서로 다른 상태로 분리되므로 $A$는 그 자체로는 예측력이 없다. 따라서 $A$를 제거한다. 우리에게 남은 상태들은 $B=\{0\}$과 $C=\{1\}$ 두 개이다.
$L=2$의 통계
다음으로 넘어가면,
- 00 다음에 1이 나올 확률은 818/1654=49.5%이다. 이는 $B$와 매우 유사하므로 B에 00을 추가한다: $B=\{0,00\}$.
- 01 다음에 1이 나올 확률은 1655/1655=100%로서 앞에 나온 어떤 경우와도 다르다. 따라서 새로운 상태 $D=\{01\}$이 추가된다.
- 10 다음에 1이 나올 확률은 837/1655=50.6%이므로 다시 $B$에 추가한다: $B=\{0,00,10\}$.
- 11 다음에 1이 나올 확률은 3378/5032=67.1%로서 지금 존재하는 어떤 상태와도 다르다. 따라서 $E=\{11\}$을 만든다.
01과 11이 다른 상태로 나뉘므로 $C=\{1\}$은 예측력이 없다. 따라서 $C$를 제거한다. 이제 우리에게 있는 상태는 $B=\{0,00,10\}$, $D=\{01\}$, $E=\{11\}$의 세 개이다.
$L=3$의 통계
마찬가지로 따져보면,
- $P(1|000) = 422/836 = 50.5\% \longrightarrow B=\{0,00,10,000\}$
- $P(1|001) = 818/818 = 100 \% \longrightarrow D=\{01,001\}$
- $P(1|010) = 0/0$
- $P(1|011) = 841/1655 = 50.8\% \longrightarrow B=\{0,00,10,000,011\}$
- $P(1|100) = 396/818 = 48.4\% \longrightarrow B=\{0,00,10,000,011,100\}$
- $P(1|101) = 837/837 = 100\% \longrightarrow D=\{01,001,101\}$
- $P(1|110) = 836/1654 = 50.5\% \longrightarrow B=\{0,00,10,000,011,100,110\}$
- $P(1|111) = 2537/3378 = 75.1\% \longrightarrow F=\{111\}$
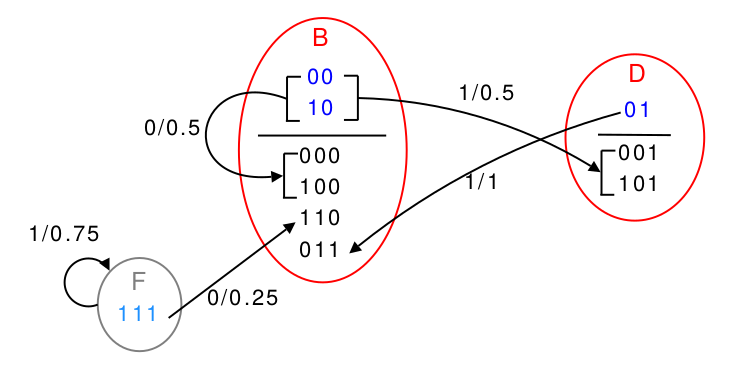
이 때 011과 111이 다른 상태로 분류되었으므로 $E=\{11\}$은 예측력을 잃어서 제거되어야 한다. 또 길이가 1인 문자열들은 길이가 2인 문자열들보다 새로운 정보를 담고 있지 않으므로 제거될 수 있다. 우리가 가지고 있는 상태는 $B=\{00,10,000,011,100,110\}$, $D=\{01,001,101\}$, $F=\{111\}$의 세 개이다.
우리는 여기까지 상태를 나누겠다고 결정해놓았으므로 이제 이 세 상태 사이의 전이를 결정해야 한다. 이 때 길이 $L_\text{max}-1$인 문자열로부터 시작하여 어느 상태로 가는지를 보는 것이 원칙이다. 예컨대 00 뒤에 0이 오면 (1/2의 확률) 000이므로 $B$에서 $B$로의 전이가 있다는 뜻이고, 나머지 1/2의 확률로 00 뒤에 1이 오면 001이 되므로 $B$에서 $D$로 가는 전이가 있다는 뜻이다.
반면 길이 $L_\text{max}$인 문자열을 가지고 이 과정을 수행하는 것은 문제가 되는데, 예컨대 011 다음에 1을 붙이고 앞의 0을 잊어버리면 (가정상 우리에겐 $L_\text{max}=3$의 기억 제한이 있으므로) 111이 되어 F로 간다고 놓을 수도 있지만, 이 경우 1이 지금까지 몇 개나 나왔었는지에 대한 정보는 영원히 사라져버리고 만다. 그러면 짝수 과정의 기본 성질은 소실될 것이다. 이는 data closure라고 불리는 일반적인 문제에 속한다.
물론 $F$처럼 어떤 상태가 길이 $L_\text{max}$인 문자열 하나만을 가지고 있다면 어쩔 수 없이 이로부터 전이를 말해야 할 것이지만 이는 예외적인 상황이다.
아래 그림은 세 상태 사이의 전이까지 그려넣은 그림이다(Cirera):
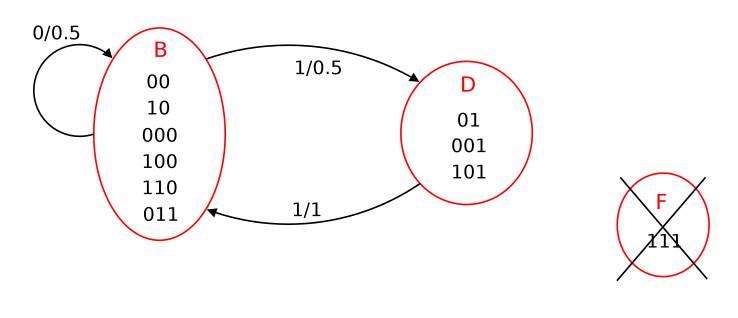
여기에서 $F$로 들어가는 전이가 없으므로 $F$는 조금만 시간이 지나도 별 역할을 하지 못하는 과도적(transient) 상태이다. 이를 그림에서 지우고 정리해서 그린다(Cirera):
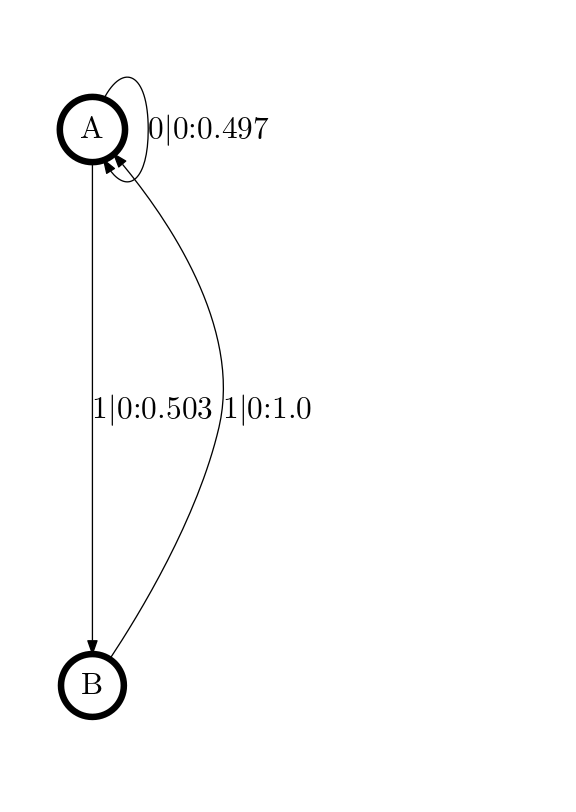
이는 제일 위에서 보여주었던 짝수 과정의 전이 도표를 성공적으로 재구축한 것이다.
코드
제안자들이 직접 개발한 CMPy1.0은 비공개이다. 그 대안으로서 David Darmon의 공개 코드가 있다: https://github.com/ddarmon/transCSSR
이를 사용하기 위해서는
- 분석하고 싶은 시계열을 data라는 디렉토리에 저장하고
- demo_CSSR.py를 편집, 실행한다.
- transCSSR_results라는 디렉토리에 생성된 .dot 파일을 그래프로 변환한다.
- .dat_results라는 확장자를 가지는 파일 안에는 그래프에 대한 더 자세한 정보가 담겨있다.
짝수 과정에 대해 실행해보면 다음과 같은 그래프를 얻는다.