Table of Contents
:
개요
주성분 분석(principal component analysis)란 데이터를 독립적인 성분들로 분해하는 기법이다. 분산이 큰 방향부터 순서대로 주축(principal axis)를 구한 다음, 몇 개의 주축들만을 사용해 데이터를 압축해서 표현할 수 있다.
이론
$N$번의 관찰로 얻어진 데이터가 있고, 각각의 데이터가 $M$개의 성분을 가진다고 하자. $n$ 번째 관찰은 $[R_{1n}, \ldots, R_{Mn}]^T$라는 열 벡터로 표현할 수 있고, 전체 데이터는 $M \times N$ 행렬 $R$로 쓸 수 있다. 여기에서 성분별 평균 $\mu_m = N^{-1} \sum_n R_{mn}$을 빼주어 새로운 행렬 $X$를 만들자: \begin{equation} X = \begin{pmatrix} R_{11} - \mu_1 & \ldots & R_{1N} - \mu_1\\ \vdots & \ddots & \vdots\\ R_{M1}-\mu_M & \ldots & R_{MN}-\mu_M \end{pmatrix}. \end{equation}
공분산(covariance) 행렬은 성분끼리의 상관 관계를 알려주는 $M \times M$의 실수 대칭 행렬이다. \begin{eqnarray} Q &=& \frac{1}{N-1} XX^T\\ &=& \frac{1}{N-1} \begin{pmatrix} X_{11} & \ldots & X_{1N}\\ \vdots & \ddots & \vdots\\ X_{M1} & \vdots & X_{MN} \end{pmatrix} \begin{pmatrix} X_{11} & \ldots & X_{M1}\\ \vdots & \ddots & \vdots\\ X_{1N} & \vdots & X_{MN} \end{pmatrix}. \end{eqnarray} 예를 들어 이 중 한 원소를 뽑아보면 다음과 같다: \begin{eqnarray} Q_{ij} &=& \frac{1}{N-1} \sum_{n=1}^N X_{in} X_{jn}\\ &=& \frac{1}{N-1} \sum_{n=1}^N (R_{in}-\mu_i) (R_{jn}-\mu_j). \end{eqnarray}
위의 공분산 행렬을 대각화하였을 때 얻는 고유값 $\lambda_1 \ge \lambda_2 \ge \ldots \ge \lambda_M$이 있고 이에 해당하는 고유 벡터 $\hat{e}_1, \hat{e}_2, \ldots, \hat{e}_M$들이 있는데 이 고유 벡터들이 주축의 방향을 가리킨다.
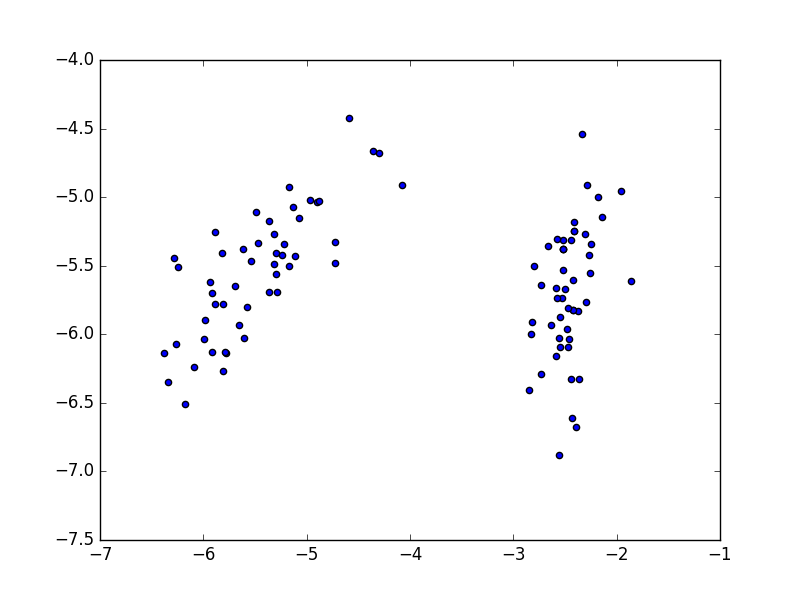
다음처럼 예제 코드를 적을 수 있다. sklearn.datasets로부터 iris 데이터를 읽어들여서 이 중 $M(=3)$차원 데이터 $N(=100)$개를 사용하자. 주성분 분석으로 얻어진 2개의 주축만을 취하고, 모든 데이터를 이 방향으로 사상시켜서 그린다. 이는 원래의 3차원 데이터를 2차원으로 압축하는 것에 해당한다.
<Code:python> from future import print_function,division from pylab import scatter,show from sklearn.datasets import load_iris from numpy.linalg import eigh # for Hermitian or symmetric matrices
iris = load_iris() M, N = 3, 100 R_transpose = iris.data[:N, :M] # R^T: N*M matrix mu = R_transpose.mean(axis=0) # average components X_transpose = R_transpose - mu
Q = X_transpose.T.dot(X_transpose)/(X_transpose.shape[0]-1) # XX^T/(N-1) eigenvalues, eigenvectors = eigh(Q) u0 = eigenvectors[:,M-1] # 1st principal axis u1 = eigenvectors[:,M-2] # 2nd principal axis scatter(R_transpose.dot(u0),R_transpose.dot(u1)) show() </Code>
특이값 분해와의 관계
특이값 분해(singular value decomposition)를 사용하면 $M \times N$ 행렬 $X$를 $X = U D V^T$로 분해할 수 있다. 이 때 $U$는 $M \times M$ 직교행렬, $V$는 $N \times N$ 직교행렬, 그리고 $D$는 대각행렬이다. $U$의 열들은 $X X^T$의 고유 벡터, 그리고 $V$의 열들은 $X^T X$의 고유 벡터들이다.
특이값 분해를 써서 아래처럼 더 간결하게 적을 수 있다. <Code:python> from future import print_function,division from pylab import scatter,show from sklearn.datasets import load_iris from numpy.linalg import svd
iris = load_iris() M, N = 3, 100 R_transpose = iris.data[:N, :M] # R^T: N*M matrix mu = R_transpose.mean(axis=0) # average components X_transpose = R_transpose - mu
U, D, V_transpose = svd(X_transpose.T, full_matrices=False) #U: M*M, V: N*N scatter(V_transpose[0,:], V_transpose[1,:]) show() </Code>
V_transpose의 행 벡터들(= V의 열 벡터들)을 바로 그려도 앞의 코드와 정성적으로 같은 결과를 얻는 까닭은, 특이값 분해에서 다음 관계가 성립하기 때문이다: $$ X \hat{v}_i = \sigma_i \hat{u}_i \longleftrightarrow X^T \hat{u}_i = \sigma_i \hat{v}_i.$$
정확히 같은 결과를 원할 경우 특이값을 곱하고 평균만큼 옮겨 주어서 다음처럼 적으면 될 것이다. <Code:python> scatter(D[0]*V_transpose[0,:]+mu.dot(U[:,0]), D[1]*V_transpose[1,:]+mu.dot(U[:,1])) </Code>
실행 결과는 아래와 같다.