양자 조화 진동자

양자 조화 진동자(quantum harmonic oscillator)는 고전적인(classical) 조화 진동자와 같은 에너지의 형태를 양자역학으로 기술하는 모형이다.

$$ \\ $$ 고전적인 조화 진동자는 다음의 'Hooke의 법칙'을 따르며 $$ F=-kx=m \frac{d^2x}{dt^2}$$

이 경우 퍼텐셜(potential) 에너지는 다음과 같다. $$V(x) = \frac{1}{2}kx^2$$

어떤 형태의 임의의 퍼텐셜을 국소적 최솟값 근처에서 어림할 때 다음과 같이 테일러 전개 (Taylor expansion)할 수 있고

$$V(x) = V(x_0) + V'(x-x_0) + \frac{1}{2}V''(x_0)(x-x_0)^2 + \ ... $$ $x_0$가 '최소점'일 때 $V'(x_0)=0$임을 통해서 포물선 식의 형태로 근사할 수 있으므로

조화 진동자는 기초적으로 중요한 모형이라고 할 수 있다.

$$ \\ $$ 그의 에너지는 고전역학으로 다음과 같이 표현되는데

$$ E = \frac{p^2}{2m} + V(x) = \frac{p^2}{2m} + \frac{1}{2}kx^2 = \frac{1}{2m}(p^2 + (m\omega x)^2) \\ \left(\because \omega \equiv \sqrt{\frac{k}{m}}\ \right)$$

양자역학에서는 $x$에 대한 공간에서 운동량 $p$를 '연산자' $$\hat{p}= \frac{\hbar}{i}\frac{d}{dx} $$

로 취급해야 하며

그 때에는 $x$와 $\hat{p}$를 교환할 수 없게 되어 다음과 같은 식을 따른다.

$$ [x,\hat{p}]\ \psi(x)=(x\hat{p}-\hat{p}x)\psi(x) = i\hbar \psi(x) \\ \therefore [x,\hat{p}]=i\hbar $$

'올림연산자'(raising operator)와 '내림연산자'(lowering operator)는 다음과 같이 정의된다.

$$\text{raising(creation) operator : } \ a^{\dagger}\equiv \sqrt{\frac{m\omega}{2\hbar}}\left( \hat{x}-\frac{i}{m\omega}\hat{p} \right) \\ \\ \text{lowering(annihilation) operator : } \ a\equiv \sqrt{\frac{m\omega}{2\hbar}}\left( \hat{x}+\frac{i}{m\omega}\hat{p} \right) \\ \\ $$

그에 따라서 다음의 교환관계도 성립한다.

$$[a,a^{\dagger}]=1 $$

$$ \\ $$ 수 연산자(number operator)는 다음과 같이 정의된다.

$$ N \equiv a^{\dagger}a$$

그에 따라서 다음의 교환관계도 마찬가지로 성립한다.

$$[N,a]=-a, \ [N,a^{\dagger}] = a^{\dagger} $$

$$ \\ $$

연산자 $N$에 대한 고유 상태를 $|n\rangle$로 나타낸다면,

$$ N | n\rangle = a^{\dagger}a |n \rangle = n | n \rangle$$ 와 같이 표현할 수 있다.

이때, $[a,a^{\dagger}]=1 $를 이용한 다음과 같은 풀이에 의해서

연산자 $a$와 $a^{\dagger}$ 의미를 알 수 있다.

$$ N a| n\rangle = [N,a] + a N |n \rangle = a N - a | n \rangle \\ a N | n \rangle - a | n \rangle = (n - 1) a | n \rangle\\ (\because \ N | n \rangle = n | n \rangle )\\ \therefore \ a |n \rangle = c_- | n-1 \rangle $$

$$\\ $$ $$ N a^{\dagger}| n\rangle = [N,a^{\dagger}] + a^{\dagger} N |n \rangle = a^{\dagger} N + a^{\dagger} | n \rangle \\ a^{\dagger} N | n \rangle + a^{\dagger} | n \rangle = (n + 1) a^{\dagger} | n \rangle\\ \\ \therefore \ a^{\dagger} |n \rangle = c_+ | n-1 \rangle $$

또한, 규격화 (normalization)을 통해서 각 계수 $c_-$와 $c_+$를 다음과 같이 결정할 수 있다.

$$a|n \rangle=\sqrt{n}|n-1\rangle \\ a^{\dagger}|n \rangle=\sqrt{n+1}|n+1\rangle$$

$$ \\ $$ 그리고 $a$와 $a^{\dagger}$의 정의에 의해서 다음의 식이 성립되어

$$ aa^{\dagger} = \frac{H}{\hbar \omega} + \frac{1}{2},\\ a^{\dagger}a = \frac{H}{\hbar \omega} - \frac{1}{2}\\ (\because \ H= \frac{1}{2m}\left[p^2 + (m\omega x)^2 \right] \ ) $$

해밀토니안 연산자 $H$를 다음과 같이 표현할 수 있음을 확인할 수 있다.

$$H =\hbar\omega\left(a^{\dagger}a+\frac{1}{2}\right)= \hbar\omega\left(N+\frac{1}{2}\right) \\ H|n\rangle = E_n|n\rangle, \ E_n = \hbar\omega\left(n+\frac{1}{2} \right)$$ $ \\ $

'결맞는 상태'는 내림 연산자 $a$의 고유 상태로 정의한다.

$$ a|\alpha\rangle=\alpha|\alpha\rangle, \quad (\alpha \text{: complex number}) $$

그에 대응되는 고유값 $\alpha$는 일반적으로 복소수이다.

$ \\ $

결맞는 상태 $| \alpha \rangle$ 를 아래와 같이 $|n \rangle$을 기저로 하여 생성한다면

$$|\alpha\rangle = \sum_{n=0}^{\infty} c_n(\alpha) |n\rangle\\ $$ 와 같이 표현할 수 있다.

계수 $c_n(\alpha)$은 다음의 과정에 따라서 구할 수 있다.

\begin{align} &a|\alpha\rangle = a\sum_{n=0}^\infty c_n(\alpha) |n\rangle = \sum_{n=0}^\infty c_n(\alpha)\ a|n\rangle \\ &\ \quad = \sum_{n=1}^\infty c_n(\alpha)\ a|n\rangle= \sum_{n=1}^\infty c_n(\alpha)\ \sqrt{n}|n-1\rangle = \sum_{n=0}^\infty c_{n+1}(\alpha)\ \sqrt{n+1}|n\rangle \quad (\because a|0\rangle=0). \\ \\ &a|\alpha\rangle = \sum_{n=0}^\infty c_{n+1}(\alpha) \sqrt{n+1} |n\rangle= \alpha | \alpha\rangle = \alpha\sum_{n=0}^\infty c_n(\alpha) |n\rangle \\ &\to \sum_{n=0} ^\infty \left[c_{n+1}(\alpha)\sqrt{n+1} - \alpha c_n(\alpha) \right]=0 \\ &\Rightarrow \ c_{n+1}(\alpha)=\frac{\alpha}{\sqrt{n+1}}c_n(\alpha)=\frac{\alpha}{\sqrt{n+1}}\frac{\alpha}{\sqrt{n}}c_{n-1}(\alpha) =\ ... \\ \\ & \therefore c_n(\alpha)=\frac{{\alpha}^n}{\sqrt{n!}}c_0(\alpha) \ \to \ |\alpha\rangle=\sum_{n=0}^\infty \frac{\alpha^n}{\sqrt{n!}} c_0(\alpha) | n\rangle \end{align}

$$ \\ $$ 이제 $c_0(\alpha)$를 규격화를 통해서 구하면 다음과 같다.

\begin{align} &1=\langle\alpha|\alpha\rangle=\langle n|n \rangle \sum_{n=0}^\infty |c_n(\alpha)|^2=\sum_{n=0}^\infty |c_n(\alpha)|^2 =\sum_{n=0}^\infty \frac{|\alpha|^{2n}}{n!} |c_0(\alpha)|^2 \\ & \ \ =|c_0(\alpha)|^2 \sum_{n=0}^\infty \boldsymbol{\frac{|\alpha|^{2n}}{n!}} =|c_0(\alpha)|^2 \boldsymbol{e^{|\alpha|^2}} \\ &\ \ \to |c_0(\alpha)|^2 =e^{-|\alpha|^2} \\ \\ & \therefore |\alpha\rangle = \sum_{n=0}^\infty c_n(\alpha) |n\rangle = \sum_{n=0}^\infty\frac{\alpha^{n}}{\sqrt{n!}}e^{-|\alpha|^2/2}|n\rangle \end{align}

아래의 '결맞는 상태'에 대해서,

$$ |\alpha\rangle = \sum_{n=0}^\infty\frac{\alpha^{n}}{\sqrt{n!}}e^{-|\alpha|^2/2}|n\rangle $$

$|n \rangle$의 상태로 발견될 확률은 다음과 같다.

$$P(n)=|\langle n | \alpha \rangle|^2=e^{-|\alpha|^2} \frac{\alpha^{2n}}{n!}$$

그런데, $|n \rangle$의 $n$은 에너지의 높고 낮음을 표현하므로

이는 $n$개의 광자를 흡수한 상태로 이해할 수 있다.

즉, $P(n)=|\langle n | \alpha \rangle|^2=e^{-|\alpha|^2} \frac{\alpha^{2n}}{n!}$는 $n$개의 광자(photon)들을 발견할 확률과 같다.

$$ \\ $$ 이를 통해, 결맞는 상태에 대해서 '평균 광자 수'가 $\langle n \rangle=\langle a^{\dagger}a \rangle=|\alpha|^2$와 같은 푸아송 분포 (Poisson distribution)를 따른다는 것을 알 수 있으며

그의 분산도 $|\alpha|^2$이다.

앞서 언급한 '고전적 모형', '수 고유 상태 ($|n \rangle $)', 그리고 '결맞는 상태 ($| \alpha \rangle$)'에 대해서

불확정성을 식으로 계산한 후에 물리적인 직관을 얻어보자.

$$ \\ $$ 설명의 편의를 위해, $m=\omega=\hbar=1$ 로 두고 $x$와 $p$에 대한 위상 평면(phase plane)을 소개하고자 한다.

고전적인 운동의 경우는 위치 $x$와 운동량 $p$를 동시에 정확히 기술할 수 있으므로

조화 진동자 모형의 운동을 위상 평면에 아래와 같이 그릴 수 있다.

(이는 1차원 용수철 운동을 떠올린다면 더 쉽게 이해할 수 있다.)

이러한 $x$와 $p$가 이루는 자취의 방정식을 수식으로 표현하자면

$\frac{1}{2}(x^2+p^2)=n$ 으로 표현할 수 있겠다.

양자 조화 진동자 (quantum harmonic oscillator)에 대한 고유 상태 $|n \rangle$에 대해서는

아래와 같은 계산 과정을 따라갈 수 있다.

\begin{align} &\ a^{\dagger}=\sqrt{\frac{m\omega}{2\hbar}}\left( x-\frac{i}{m\omega}\hat{p} \right), \ a=\sqrt{\frac{m\omega}{2\hbar}}\left( x+\frac{i}{m\omega}\hat{p} \right) \\ \\ &\ a^{\dagger}|n \rangle=\sqrt{n+1}|n+1\rangle, \ a|n \rangle=\sqrt{n}|n-1\rangle \\ \\ &\to x=\sqrt{\frac{\hbar}{2m\omega}}(a+a^{\dagger}), \ \hat{p}=-i\sqrt{\frac{\hbar m\omega}{2}}(a-a^{\dagger}) \\ & \ \langle n|x|n \rangle = \langle n|\sqrt{\frac{\hbar}{2m\omega}}(a+a^{\dagger})|n \rangle =0 \\ & \ \langle n|\hat{p}|n \rangle = \langle n|-i\sqrt{\frac{\hbar m\omega}{2}}(a-a^{\dagger})|n \rangle =0 \quad (\because \ \text{orthogonality}) \\ \\ & \ \langle n|x^2|n \rangle = \langle n|\frac{\hbar}{2m\omega}(a+a^{\dagger})(a+a^{\dagger})|n \rangle \\ & \ \ \quad = \langle n|\frac{\hbar}{2m\omega}(aa^{\dagger}+a^{\dagger}a)|n \rangle = \frac{\hbar}{m\omega}\left(n+\frac{1}{2} \right) \\ & \ \langle n|\hat{p}^2|n \rangle = \langle n|-\frac{\hbar m\omega}{2}(a-a^{\dagger})(a-a^{\dagger})|n\rangle \\ & \ \ \quad = \langle n| \frac{\hbar m\omega}{2}(aa^{\dagger}+a^{\dagger}a)|n\rangle = \hbar m\omega \left(n+\frac{1}{2}\right) \\ \\ & \sigma_x \sigma_p =\hbar^2 \left(n+\frac{1}{2}\right)^2 \ge \left( \frac{\hbar}{2} \right)^2 \quad \left(\because \ \sigma_A = \langle A^2 \rangle - \langle A \rangle ^2 \right) \end{align}

즉, $n$이 클수록 불확정성(uncertainty)가 더 크다.

$$ \\ $$ 위에서 $ \langle n|x^2|n \rangle = \frac{\hbar}{m\omega}\left(n+\frac{1}{2} \right), \ \langle n|\hat{p}^2|n \rangle = \hbar m\omega \left(n+\frac{1}{2}\right) $ 의 결과를 고려한다면, 다음이 성립함을 알 수 있다.

$$ n \le \frac{1}{2}(x^2+p^2) \le n+1 $$

또한, $\langle n|x|n \rangle=\langle n|\hat{p}|n \rangle=0$ 이 성립한다.

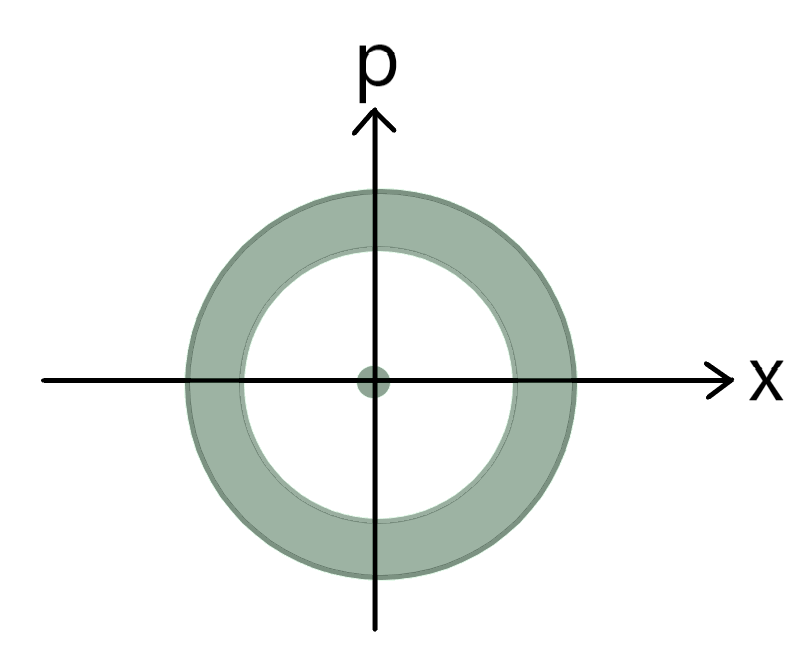
$$ \\ $$ 이를 위상 평면에서 표현하면 다음과 같다.

위의 폭은 $ \sigma_x \sigma_p =\hbar^2 \left(n+\frac{1}{2}\right)^2 \ge \left( \frac{\hbar}{2} \right)^2 $의 불확정성에 의한 것이다.

앞서 언급한 결맞는 상태 $a|\alpha\rangle=\alpha|\alpha\rangle \ \ (\alpha \in \mathbb{C}) $ 의 경우는 어떻게 될까? 아래와 같이 계산해보자.

$$x=\sqrt{\frac{\hbar}{2m\omega}}(a+a^{\dagger}), \ \hat{p}=-i\sqrt{\frac{\hbar m\omega}{2}}(a-a^{\dagger}) ,\\ \langle\alpha| x |\alpha\rangle=\sqrt{\frac{\hbar}{2m \omega}}\left(\ (\langle\alpha| a^{\dagger})+(a|\alpha\rangle)\ \right) \\ = \sqrt{\frac{\hbar}{2m \omega}}(\alpha^* +\alpha) \\ \\ \langle\alpha| \hat{p} |\alpha\rangle=-i\sqrt{\frac{\hbar m\omega}{2}} \left(\ (-\langle\alpha| a^{\dagger})+(a|\alpha\rangle)\ \right) \\ =-i\sqrt{\frac{\hbar m\omega}{2}}(-\alpha^*+\alpha)$$

$\langle n|x|n \rangle$와 $\langle n|\hat{p}|n \rangle$가 $0$이 아니라는 점을 기억해두는 편이 좋다.

$$ \\ $$

\begin{align} &\ \langle \alpha|x^2|\alpha \rangle = \langle \alpha|\frac{\hbar}{2m\omega}(a+a^{\dagger})(a+a^{\dagger})|\alpha \rangle \\ & \ \ \quad = \frac{\hbar}{2m \omega}\langle \alpha |(aa +aa^{\dagger}+a^{\dagger}a+a^{\dagger}a^{\dagger})|\alpha \rangle\\ & \ \ \quad = \frac{\hbar}{2m \omega}\langle \alpha |(aa +2a^{\dagger}a+1+a^{\dagger}a^{\dagger})|\alpha \rangle\\ &\qquad (\because \ [a,a^{\dagger}]=aa^{\dagger}-a^{\dagger}a=1) \\ & \ \ \quad = \frac{\hbar}{2m \omega} \left( \alpha^2 +2\alpha^*\alpha +1+{\alpha^*}^2 \right) \\ \\ & \ \langle \alpha|\hat{p}^2|\alpha \rangle = \langle \alpha|-\frac{\hbar m\omega}{2}(a-a^{\dagger})(a-a^{\dagger})|\alpha\rangle \\ & \ \ \quad =-\frac{\hbar m \omega}{2} \langle\alpha |(aa-aa^{\dagger}-a^{\dagger}a+a^{\dagger}a^{\dagger}) | \alpha\rangle \\ & \ \ \quad =-\frac{\hbar m \omega}{2} \langle\alpha |(aa-2a^{\dagger}a-1+a^{\dagger}a^{\dagger}) | \alpha\rangle \\ & \ \ \quad =-\frac{\hbar m \omega}{2} \left(\alpha^2-2\alpha^*\alpha-1+{\alpha^*}^2 \right) \\ & \sigma_x \sigma_p =(\frac{\hbar}{2m\omega})(\frac{\hbar m\omega}{2})=\left(\frac{\hbar}{2}\right)^2 \end{align}

결맞는 상태(coherent state)의 불확정성(uncertainty)은 $n$의 크기와 무관하며,

$(\frac{\hbar}{2})^2$의 값에 따라 '최소' 불확정성의 상태(minimum uncertainty state) 이다.

$$ \\ $$

또한, 계산한 $\langle x \rangle = \langle\alpha| x |\alpha\rangle$와 $\langle\hat{p}\rangle=\langle\alpha| \hat{p} |\alpha\rangle$의 결과를 고려하면

($m=\omega=\hbar=1$로 두었을 때) 다음이 성립함을 알 수 있다.

$$ \alpha = \frac{1}{\sqrt{2}} (\langle x \rangle + i\langle \hat{p} \rangle) $$

이를 위상 평면에 아래와 같이 나타낼 수 있다.

즉, 마치 고전적인 극한에서 불확정성을 표현하는 면적이 점으로 표현되는 것과 같이

위의 '자취의 반지름'이 ($\alpha$) 매우 클 경우에는 그 불확정성의 면적 크기 $(\frac{\hbar}{2})^2$를 상대적으로 무시 가능하므로

결맞는 상태가 $(x,p)$ 평면 상에서 고전적인 조화 진동자를 모방한다고 표현할 수 있다.

$$ \\ $$

다음의 결맞는 상태의 식에

$$|\alpha\rangle = \sum_{n=0}^\infty c_n(\alpha) |n\rangle = \sum_{n=0}^\infty\frac{\alpha^{n}}{\sqrt{n!}}e^{-|\alpha|^2/2}|n\rangle\\ = \sum_{n=0}^\infty\frac{\alpha^{n}}{\sqrt{n!}}e^{-\alpha^* \alpha/2}|n\rangle $$

'시간 변화 연산자(time evolution operator)'인 $e^{-iHt/\hbar}$ 를 걸어보자.

\begin{align} e^{-iHt/\hbar}|\alpha \rangle = &\sum_{n=0}^\infty\frac{\alpha^{n}}{\sqrt{n!}}e^{-iHt/\hbar} |n\rangle e^{-\alpha^* \alpha/2} \\ = &\sum_{n=0}^\infty\frac{\alpha^{n}}{\sqrt{n!}}e^{-i\hbar \omega (n+\frac{1}{2})t/\hbar} |n\rangle e^{-\alpha^* \alpha/2} \\ = &\sum_{n=0}^\infty\frac{\alpha^{n}}{\sqrt{n!}}e^{-in\omega t} |n\rangle e^{-\alpha^* \alpha/2}e^{-i\omega t/2 } \\ = &\sum_{n=0}^\infty\frac{(\alpha e^{-i\omega t})^n}{\sqrt{n!}}|n\rangle e^{-\alpha^* \alpha/2}e^{-i\omega t/2 } \\ = &|\alpha e^{-i\omega t }\rangle e^{-i\omega t/2 } \end{align}

$$ \\ $$ 즉, $e^{-iHt/\hbar} | \alpha \rangle = |\alpha e^{-i\omega t }\rangle e^{-i\omega t/2 }$의 관계식이 성립한다.

$$ \\ $$ 이러한 결과와 오일러 공식(Euler formula), 그리고 $\alpha$와 $\langle x \rangle, \langle\hat{p}\rangle$의 관계식을 떠올려 볼 때 $$ e^{-i\omega t}=\cos(\omega t)-i\sin(\omega t) \\ \alpha = \frac{1}{\sqrt{2}} (\langle x \rangle + i\langle \hat{p} \rangle), \ i=e^{\pi/2} $$

(위에서 살펴본 그림과 같이) 고전적인 극한($\alpha \gg 1$)에서는 결맞는 상태를 위상 평면 상에서 이해할 때

불확정성을 무시 가능하며 운동하는 입자로 취급할 수 있다는 것을 알 수 있다.

$$ \\ $$

Hitoshi Murayama, Jan27 151 Coherent state, QFT on 1D lattice, 2021. (lecture of Prof. Hitoshi Murayama)