단일 입자 양자역학

This is an old revision of the document!

단일 입자 양자역학을 통해서 '빛 보다 더 빠르게 움직이는 입자의 진폭(amplitude)'를 구해보고자 한다.

상대성이론에 따라서 빛 보다 빠르게 움직일 수 있는 것은 없다. 그렇다면 그 진폭은 $0$ 이어야 할 것인데, 실제로 그러한지 확인해고자 한다.

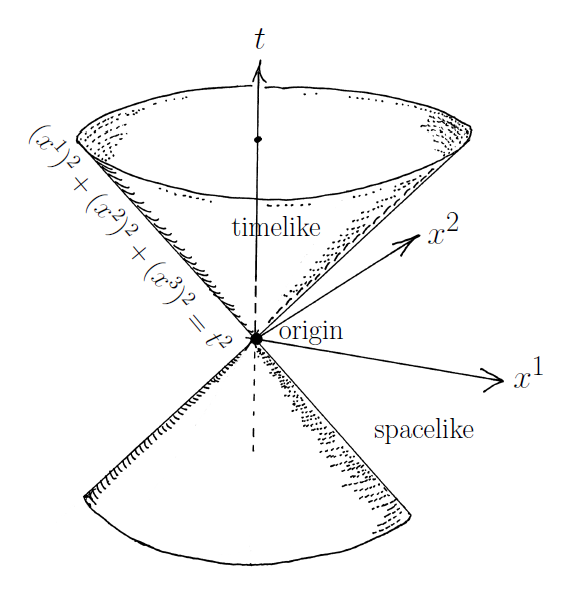
$\\$ 우선 '빛 보다 빠른 입자'를 '빛원뿔(light cone)'위에서 더 쉽게 이해할 수 있다.

즉, 특수상대성 이론에 위배되지 않는 (허용되는) 경로(time-like라고 부른다)는 원뿔의 안쪽에 해당하며 다음을 만족하는 것이다.

$|x|^2 =t^2-(x^1)^2-(x^2)^2-(x^3)^2 >0$

광자(photon)의 경우는 $|x|^2 =t^2-(x^1)^2-(x^2)^2-(x^3)^2 =0$ 으로서, 원뿔면 위에 놓이는 경로를 따라 간다.

$\\$ 이때, $|x|^2 =t^2-(x^1)^2-(x^2)^2-(x^3)^2 <0$ 의 경로(space-like라고 부른다)를 따라가는 경로는 허용가능하지 않는 것이다.

그럼 해당 경로에 대해서, 다음과 같은 양을 정의하고

$\mathcal{A}=\langle \boldsymbol{x} |e^{-i\hat{H}t}| \boldsymbol{x}=0\rangle$

$\begin{align} \mathcal{A}=\langle \boldsymbol{x} |e^{-i\hat{H}t}| \boldsymbol{x}=0\rangle &= \int d^3p \langle \boldsymbol{x} |e^{-i\hat{H}t}|\boldsymbol{p}\rangle \langle \boldsymbol{p}|\boldsymbol{x}=0 \rangle \\ &= \int d^3p \langle \boldsymbol{x} | \boldsymbol{p} \rangle e^{-iE_pt} \frac{1}{(2\pi)^{3/2}}e^{-i\boldsymbol{p}\cdot 0} \\ &= \int d^3p \frac{1}{(2\pi)^3}e^{i\boldsymbol{p}\cdot \boldsymbol{x}}e^{-iE_p t}. \end{align}$ $| \mathcal{A}| ^2$ 이 0이 아닌지를 확인해보자.

$\\$ 첫 번째 줄에서는 완전 집합(complete set)의 성질인 $1=\int d^ep | \boldsymbol{p} \rangle \langle \boldsymbol{p}|$ 을 이용하였다.

두 번째 줄로 넘어갈 때, $e^{-i\hat{H}t}$ 를 $|\boldsymbol{p}\rangle$ 에 걸어줌으로써 고유값을 $e^{-iE_pt}$ 로 얻었다. 또한, 다음의 식을 이용하였다.

$\langle \boldsymbol{x} | \boldsymbol{p}\rangle =\frac{1}{(2\pi)^{3/2}}e^{i\boldsymbol{p}\cdot \boldsymbol{x}}$ (규격화 상수(normalization constant)가 정확한 값일 필요는 없다. $\mathcal{A}$ 가 0인지, 그렇지 않은지만 파악하면 되기 때문이다.)

이제 해야할 것은, 다음의 적분 계산을 $|x|^2 =t^2-(x^1)^2-(x^2)^2-(x^3)^2 <0$ (space-like) 에 해당하는 간격(interval)에 대해서 풀이하는 것이다.

$\begin{align} \mathcal{A}=\int d^3p \frac{1}{(2\pi)^3}e^{i\boldsymbol{p}\cdot \boldsymbol{x}}e^{-iE_p t}. \end{align}$ 이러한 적분식을 구면 좌표계 (spherical polars)로 다음과 같이 변환하자. $\begin{align} \mathcal{A} &= \int _0 ^{2\pi} d\phi \int^\infty _0 \frac{d|\boldsymbol{p} |}{(2\pi)^3}|\boldsymbol{p}|^2 \int^{\pi} _{0} d\theta e^{i\boldsymbol{p}\cdot \boldsymbol{x}}e^{-iE_p t} \\ &= \int _0 ^{2\pi} d\phi \int^\infty _0 \frac{d|\boldsymbol{p} |}{(2\pi)^3}|\boldsymbol{p}|^2 \int^{-1} _{1} (-du) e^{i|\boldsymbol{p}||\boldsymbol{x}|u}e^{-iE_p t} \\ &= \frac{1}{{(2\pi)^3}}\int _0 ^{2\pi} d\phi \int^\infty _0 d|\boldsymbol{p} |\ |\boldsymbol{p}|^2 \int^{1} _{-1} du e^{i|\boldsymbol{p}||\boldsymbol{x}|u}e^{-iE_p t} \\ &= \frac{1}{(2\pi)^3}(2\pi)\int^\infty _0 d|\boldsymbol{p} |\ |\boldsymbol{p}|^2 \left( \frac{1}{i(|\boldsymbol{p}||\boldsymbol{x}|)} \right)\left[e^{i|\boldsymbol{p}||\boldsymbol{x}|u}\right]_{-1}^{1}\ e^{-iE_p t} \\ &= \frac{-i}{(2\pi)^2|\boldsymbol{x}|}\int^\infty _0 d|\boldsymbol{p} |\ |\boldsymbol{p}| \left[e^{i|\boldsymbol{p}||\boldsymbol{x}|}-e^{-i|\boldsymbol{p}||\boldsymbol{x}|}\right] \ e^{-iE_p t} \\ \end{align}$ 위의 식을 풀이할 때, $\cos\theta \equiv u \to -du=\sin\theta d\theta$ 를 이용하였다.

구면 좌표계의 야코비안(Jacobian)이 $r^2 \sin\theta$ 임을 참고하자.

$\\$ (참고로, 위의 계산에서 아직 $|x|^2 =t^2-(x^1)^2-(x^2)^2-(x^3)^2 <0$ 라는 조건은 대입하지 않았다.) $\\$ 위에서 마지막 줄의 적분식을 두 항으로 분리한 뒤, 적분 범위를 아래와 같이 바꿔주면 보다 간단해진다.

$\begin{align} \mathcal{A} &= \frac{-i}{(2\pi)^2|\boldsymbol{x}|}\int^\infty _0 d|\boldsymbol{p} |\ |\boldsymbol{p}| \left[e^{i|\boldsymbol{p}||\boldsymbol{x}|}-e^{-i|\boldsymbol{p}||\boldsymbol{x}|}\right] \ e^{-iE_p t} \\ &= \frac{-i}{(2\pi)^2|\boldsymbol{x}|}\left(\int^\infty _0 d|\boldsymbol{p} |\ |\boldsymbol{p}| e^{i|\boldsymbol{p}||\boldsymbol{x}|} \ e^{-iE_p t} - \int^\infty _0 d|\boldsymbol{p} |\ |\boldsymbol{p}| e^{-i|\boldsymbol{p}||\boldsymbol{x}|} \ e^{-iE_p t}\right) \\ &= \frac{-i}{(2\pi)^2|\boldsymbol{x}|}\left(\int^\infty _0 d|\boldsymbol{p} |\ |\boldsymbol{p}| e^{i|\boldsymbol{p}||\boldsymbol{x}|} \ e^{-iE_p t} - \int^{-\infty }_0 (d(-|\boldsymbol{p} |)\ (-|\boldsymbol{p}|) e^{i|\boldsymbol{p}||\boldsymbol{x}|} \ e^{-iE_p t}\right) \\ &= \frac{-i}{(2\pi)^2|\boldsymbol{x}|}\left(\int^\infty _0 d|\boldsymbol{p} |\ |\boldsymbol{p}| e^{i|\boldsymbol{p}||\boldsymbol{x}|} \ e^{-iE_p t} + \int^{0}_{-\infty } d|\boldsymbol{p} |\ |\boldsymbol{p}| e^{i|\boldsymbol{p}||\boldsymbol{x}|} \ e^{-iE_p t}\right) \\ &= \frac{-i}{(2\pi)^2|\boldsymbol{x}|}\left(\int^\infty _{-\infty } d|\boldsymbol{p} |\ |\boldsymbol{p}| e^{i|\boldsymbol{p}||\boldsymbol{x}|} \ e^{-it\sqrt{|\boldsymbol{p}|^2 + m^2}} \right) \\ \end{align}$ 두 번째 줄에서 세 번째 줄로 넘어갈 때, $|p|$ 에 대한 적분을 $-|p|$ 에 대한 것으로 바꿔주었다.

또한, $E_p = \sqrt{|\boldsymbol{p}|^2 + m^2}$ 을 대입하였다.

$\\$ 위의 적분을 풀이하는 수학적인 방법은 복소(complex) 적분이다.

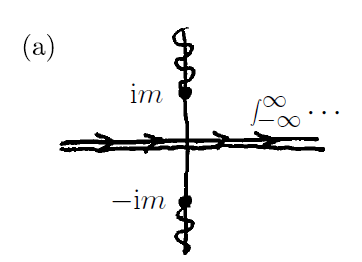
우리가 계산하고자 하는 적분은 $|\boldsymbol{p}|$ 의 $-\infty$ 부터 $\infty$ 까지의 범위에 대한 적분이므로

복소평면에서 아래와 같은 경로를 따라서 다음의 적분을 계산해야 한다.

$\mathcal{A} = \frac{-i}{(2\pi)^2|\boldsymbol{x}|}\left(\int^\infty _{-\infty } d|\boldsymbol{p} |\ |\boldsymbol{p}| e^{i|\boldsymbol{p}||\boldsymbol{x}|} \ e^{-it\sqrt{|\boldsymbol{p}|^2 + m^2}} \right) \\$

(허수축이 $\pm im$ 에서 잘린(cut) 이유는, 시간 연산자(time operator)의 고유값에 해당하는 $e^{-iE_pt}$ 의 지수는 허수이기 때문이다.

$\\$ 이때, '코시의 정리(Cauchy's theorem)'를 이용한다면 적분을 보다 원활하게 풀이할 수 있다.

'코시의 정리'란, 임의의 복소수 $z$ 에 대한 함수 $f(z)$ 가 경로 $C$ 와 그 내부에서 해석적(anaylytic)일 때, 다음의 식을 만족한다는 것이다.

$\oint_C dz\ f(z) = 0.$

즉, 경로 $C$ 내부에서 적분되는 함수 $f(z)$ 가 해석적이지 않은 특이점이 포함되지 않는다면

해당 적분은 시작점과 종점에만 의존한다.

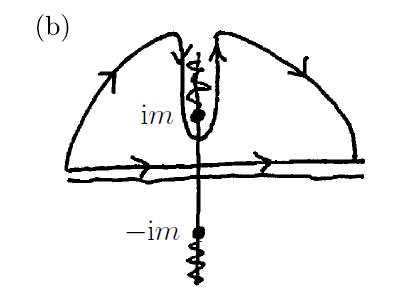
$\\$ 이때, 다음의 그림의 닫힌 곡선 안에서는 특이점이 존재하지 않는다.

따라서 우리의 적분을 반원 위쪽을 지나는 경로에 대한 적분으로 바꾸는 것이 가능하다.

$\\$ 또한, '조르당의 보조 정리(Jordan’s lemma)'에 따르면, 반원의 크기가 커질수록

반원을 지나는 적분의 (총 적분에 대한) 기여분은 $0$ 에 근접한다.

('조르당의 보조 정리'는 이번 게시글 맨 아래에 보충 설명하였다.)

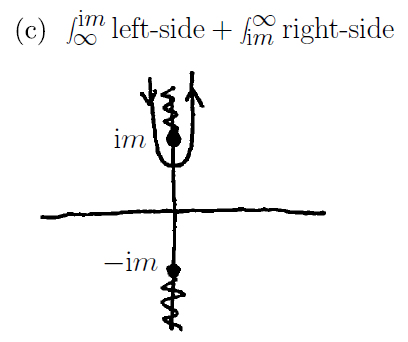
$\\$ 따라서, 유의미한 적분 경로는 아래의 그림과 같다.

$\\$

조르당의 보조 정리란,

$(1) a>0$ 이며

$(2) f(z)$ 가 $\lim_{R \to \infty} |f(Re^{i\theta})|=0$ 을 만족하는(well-behaved) 함수일 때,

'무한한 크기를 가지며 양의 허수축에 정의되는 반원'을 따라서 다음의 적분을 계산한 결과는 $0$ 이라는 것이다.

$\int_{-\infty}^{\infty} dz\ f(z)e^{iaz}$

$\\$ 앞서 설명한 경우에서는, 아래의 적분에서

$\mathcal{A} = \frac{-i}{(2\pi)^2|\boldsymbol{x}|}\left(\int^\infty _{-\infty } d|\boldsymbol{p} |\ |\boldsymbol{p}| e^{i|\boldsymbol{p}||\boldsymbol{x}|} \ e^{-it\sqrt{|\boldsymbol{p}|^2 + m^2}} \right) \\$

$a$ 가 $|x|$ 이고 $f(z)$ 는 $|\boldsymbol{p}| e^{-it\sqrt{|\boldsymbol{p}|^2 + m^2}}$ 에 대응된다.

$|x|$ 는 공간(space)에 대해 정의되는 값으로서 $0$ 보다 크고, 함수 $|\boldsymbol{p}| e^{-it\sqrt{|\boldsymbol{p}|^2 + m^2}}$ 의 값을 $|p|=z=Re^{i\theta}$ 로 두고 $R$ 의 값을 증가시켜서 보면

$z$ 의 허수부의 값도 증가할 것이다.

따라서, 아래와 같이 ( $\exp$ 함수의 지수는 실수부와 허수부를 모두 포함하므로) 허수부의 영향만을 살펴보면

$z\exp\left[{-it\sqrt{{\text{\{i(Im[z])}\}}^2 + m^2}}\right]=z\exp\left[{-it\sqrt{-\text{Im}[Re^{i\theta}]+ m^2}}\right]\\ =z\exp\left[{-it\sqrt{-R\sin \theta +m^2}}\right] \\ =z\exp\left[{-t\sqrt{R\sin \theta - m^2}}\right] \\ (\because i=\sqrt{-1})$