위에서 $n$개의 복제본에 대한 자유에너지를 다음처럼 적었다: $$ -\beta[f] = \lim_{n\rightarrow0}\left\{-\frac{\beta^2J^2}{4n}\sum_{\alpha\neq\beta}q_{\alpha\beta}^2 - \frac{\beta J_0}{2n}\sum_\alpha m_\alpha^2 + \frac14\beta^2J^2+\frac1n\ln\text{Tr}' e^L \right\}. $$

여기서 $h=0$으로 놓고 $\beta Jq_{\alpha\beta} \equiv y^{\alpha\beta}$와 $\sqrt{\beta J_0}m_\alpha \equiv x^\alpha$을 정의하면 자유에너지는

$$ [f] = -\frac{\beta J^2}{4} - \lim_{n\rightarrow0}\frac{1}{\beta n}\left\{-\sum_{\alpha\beta}\frac12(y^{\alpha\beta})^2 - \sum_\alpha\frac12(x^\alpha)^2 + \ln\text{Tr}' \exp \left(\beta J\sum_{\alpha<\beta}y^{\alpha\beta}S^\alpha S^\beta + \sqrt{\beta J_0} \sum_\alpha x^\alpha S^\alpha\right) \right\} $$

가 된다. 복제 대칭해가 안정적인지를 보려면 질서 변수들이 복제 대칭해를 조금 벗어나도록 하고 이들의 계수의 부호를 보면 될 것이다. 즉 $$ x^\alpha = x+\epsilon^\alpha,\quad y^{\alpha\beta} = y + \eta^{\alpha\beta} $$ 로 두고 $\eta^{\alpha\beta}$, $\epsilon^\alpha$로 전개할 것이다. 먼저 $\ln\text{Tr}' \exp$항은 $$ \ln\text{Tr}' \exp\left(L_0+\beta J\sum_{\alpha<\beta}\eta^{\alpha\beta}S^\alpha S^\beta + \sqrt{\beta J_0}\sum_\alpha \epsilon^\alpha S^\alpha\right) $$

인데, 여기서 $L_0 = \beta Jy\sum_{\alpha<\beta}S^\alpha S^\beta + \sqrt{\beta J_0}x\sum_\alpha S^\alpha$로, $\epsilon^\alpha$ 및 $\eta^{\alpha\beta}$와는 상관없는 항이다. 그러므로 $L_0$를 빼고 $\exp$항을 2차항까지 전개하면 ($e^x = 1+x+x^2/2 + \ldots$)

\begin{align*} &\ln\text{Tr}' \exp\left(L_0+\beta J\sum_{\alpha<\beta}\eta^{\alpha\beta}S^\alpha S^\beta + \sqrt{\beta J_0}\sum_\alpha\epsilon^\alpha S^\alpha\right)\\ =&\ln\text{Tr}'e^{L_0}\left[1+\beta J\sum_{\alpha<\beta}\eta^{\alpha\beta}S^\alpha S^\beta + \sqrt{\beta J_0}\sum_\alpha\epsilon^\alpha S^\alpha+\frac12\left(\beta J\sum_{\alpha<\beta}\eta^{\alpha\beta}S^\alpha S^\beta + \sqrt{\beta J_0}\sum_\alpha\epsilon^\alpha S^\alpha\right)^2\right]\\ =&\ln\left[\text{Tr}'e^{L_0}+\text{Tr}'e^{L_0}\left(\beta J\sum_{\alpha<\beta}\eta^{\alpha\beta}S^\alpha S^\beta + \sqrt{\beta J_0}\sum_\alpha\epsilon^\alpha S^\alpha\right)+\frac12\text{Tr}'e^{L_0}\left\{\left(\beta J\sum_{\alpha<\beta}\eta^{\alpha\beta}S^\alpha S^\beta + \sqrt{\beta J_0}\sum_\alpha\epsilon^\alpha S^\alpha\right)^2\right\}\right] \end{align*} 여기서 $\langle A\rangle_{L_0}=\text{Tr}'(e^{L_0}A)/\text{Tr}'e^{L_0}$로 쓰면 위 식은 \begin{align*} =&\ln\text{Tr}'e^{L_0}+\ln\left[1+\left\langle\beta J\sum_{\alpha<\beta}\eta^{\alpha\beta}S^\alpha S^\beta + \sqrt{\beta J_0}\sum_\alpha\epsilon^\alpha S^\alpha\right\rangle_{L_0}+\frac12\left\langle\left(\beta J\sum_{\alpha<\beta}\eta^{\alpha\beta}S^\alpha S^\beta + \sqrt{\beta J_0}\sum_\alpha\epsilon^\alpha S^\alpha\right)^2\right\rangle_{L_0}\right] \end{align*} 로 쓸 수 있고 $\ln(1+\langle x\rangle + \frac12\langle x\rangle^2+\cdots) = \langle x\rangle+\frac12(\langle x^2\rangle-\langle x\rangle^2)+\cdots$임과 $\epsilon^\alpha$ 및 $\eta^{\alpha\beta}$에 대한 1차항들은 극값 조건에 의해 사라진다는 조건을 적용하면 최종적으로 \begin{align*} &\ln\text{Tr}' \exp\left(L_0+\beta J\sum_{\alpha<\beta}\eta^{\alpha\beta}S^\alpha S^\beta + \sqrt{\beta J_0}\sum_\alpha\epsilon^\alpha S^\alpha\right)\\ =& \ln\text{Tr}'e^{L_0} + \frac12\beta^2J^2\sum_{\alpha<\beta}\sum_{\gamma<\delta}\eta^{\alpha\beta}\eta^{\gamma\delta}\left(\left\langle S^\alpha S^\beta S^\gamma S^\delta\right\rangle_{L_0}-\left\langle S^\alpha S^\beta \right\rangle_{L_0}\left\langle S^\gamma S^\delta \right\rangle_{L_0}\right)\\ &+ \beta J\sqrt{\beta J_0}\sum_{\alpha<\beta}\sum_\gamma\eta^{\alpha\beta}\epsilon^\gamma\left(\left\langle S^\alpha S^\beta S^\gamma\right\rangle_{L_0}-\left\langle S^\alpha S^\beta\right\rangle_{L_0}\left\langle S^\gamma\right\rangle_{L_0}\right) + \frac12 \beta J_0\sum_{\alpha\beta}\epsilon^\alpha\epsilon^\beta\left(\left\langle S^\alpha S^\beta\right\rangle_{L_0}-\left\langle S^\alpha\right\rangle_{L_0}\left\langle S^\beta\right\rangle_{L_0}\right) \end{align*} 가 된다. $\epsilon^\alpha$ 및 $\eta^{\alpha\beta}$의 2차항에 해당하는 성분을 모아 $\Delta$라고 쓰면 자유에너지를 $$\left[f\right] = -\frac{\beta J^2}{4} - \lim_{n\rightarrow0}\frac1{\beta n}\left\{-\frac14n(n-1)y^2-\frac12nx^2-\Delta\right\}$$ 의 꼴로 쓸 수 있고, \begin{align*} \Delta=&\frac12\sum_{\alpha<\beta}\sum_{\gamma<\delta}\eta^{\alpha\beta}\eta^{\gamma\delta}\left[\delta_{(\alpha\beta)(\gamma\delta)}-\beta^2J^2\left(\left\langle S^\alpha S^\beta S^\gamma S^\delta\right\rangle_{L_0}-\left\langle S^\alpha S^\beta \right\rangle_{L_0}\left\langle S^\gamma S^\delta \right\rangle_{L_0}\right)\right]\\ &+ \beta J\sqrt{\beta J_0}\sum_{\alpha<\beta}\sum_\gamma\eta^{\alpha\beta}\epsilon^\gamma\left(\left\langle S^\alpha S^\beta\right\rangle_{L_0}\left\langle S^\gamma\right\rangle_{L_0}-\left\langle S^\alpha S^\beta S^\gamma\right\rangle_{L_0}\right) + \frac12 \sum_{\alpha\beta}\epsilon^\alpha\epsilon^\beta\left[\delta_{\alpha\beta}-\beta J_0\left(\left\langle S^\alpha S^\beta\right\rangle_{L_0}-\left\langle S^\alpha\right\rangle_{L_0}\left\langle S^\beta\right\rangle_{L_0}\right)\right] \end{align*} 이다. 오해의 여지가 없으므로 앞으로 $\langle \cdots\rangle_{L_0}$을 $\langle\cdots\rangle$로 쓰자. 이제 안정성을 논할 차례인데 $\Delta$는 $\epsilon^\alpha$ 및 $\eta^{\alpha\beta}$에 대한 2차항 뿐 아니라 교차항도 포함하고 있으므로 벡터 $$ \vec\mu=\begin{pmatrix} \{\epsilon^\alpha\}\\ \{\eta^{\alpha\beta}\} \end{pmatrix} $$ 를 도입해 다음과 같은 2차 형식으로 쓸 수 있고, $$\Delta=\vec\mu^TG\vec\mu$$ 해의 안정성은 이 행렬 $G$의 고윳값의 부호를 통해 살펴볼 수 있다. 만약 모든 고윳값이 양수이면, 복제 대칭해가 극솟값이므로 복제 대칭해는 안정적일 것이다. 행렬 $G$의 각 성분은 $\epsilon^\alpha$, $\eta^{\alpha\beta}$의 계수로부터 알아낼 수 있는데 예를 들어 $\epsilon^\alpha\epsilon^\beta$항으로부터 \begin{align*} G_{\alpha\alpha} &= 1-\beta J_0(1-\langle S^\alpha\rangle^2)\\ G_{\alpha\beta} &= -\beta J_0(\langle S^\alpha S^\beta\rangle-\langle S^\alpha\rangle\langle S^\beta\rangle) \end{align*} 임을 알 수 있다. 마찬가지로 가능한 2차항의 조합을 모두 생각한다면 행렬 $G$의 성분을 다음과 같이 모두 표현할 수 있다. \begin{align*} G_{(\alpha\beta)(\alpha\beta)}&= 1-\beta^2J^2(1-\langle S^\alpha S^\beta\rangle^2)\\ G_{(\alpha\beta)(\alpha\gamma)}&= -\beta^2J^2(\langle S^\beta S^\gamma\rangle - \langle S^\alpha S^\beta\rangle\langle S^\alpha S^\gamma\rangle)\\ G_{(\alpha\beta)(\gamma\delta)}&= -\beta^2J^2(\langle S^\alpha S^\beta S^\gamma S^\delta\rangle-\langle S^\alpha S^\beta\rangle\langle S^\gamma S^\delta\rangle)\\ G_{\alpha(\alpha\beta)} &= \beta J\sqrt{\beta J_0}(\langle S^\alpha\rangle\langle S^\alpha S^\beta\rangle-\langle S^\beta\rangle)\\ G_{\gamma(\alpha\beta)} &= \beta J\sqrt{\beta J_0}(\langle S^\gamma\rangle\langle S^\alpha S^\beta\rangle-\langle S^\alpha S^\beta S^\gamma\rangle) \end{align*} 그리고 복제 대칭성을 가정하고 있으므로 \begin{align*} \langle S^\alpha\rangle&\equiv m=\int Dz \tanh\beta\tilde H(z)\\ \langle S^\alpha S^\beta\rangle&\equiv q=\int Dz \tanh^2\beta\tilde H(z)\\ \langle S^\alpha S^\beta S^\gamma\rangle&\equiv t=\int Dz \tanh^3\beta\tilde H(z)\\ \langle S^\alpha S^\beta S^\gamma S^\delta\rangle&\equiv r=\int Dz \tanh^4\beta\tilde H(z) \end{align*} 로 쓰면 각 성분은 \begin{align*} G_{\alpha\alpha} &\equiv A = 1-\beta J_0(1-m^2)\\ G_{\alpha\beta} &\equiv B=-\beta J_0(q-m^2)\\ G_{(\alpha\beta)(\alpha\beta)}&\equiv P=1-\beta^2J^2(1-q^2)\\ G_{(\alpha\beta)(\alpha\gamma)}&\equiv Q=-\beta^2J^2(q-q^2)\\ G_{(\alpha\beta)(\gamma\delta)}&\equiv R=-\beta^2J^2(r-q^2)\\ G_{\alpha(\alpha\beta)} &\equiv C=\beta J\sqrt{\beta J_0}(mq-m)\\ G_{\gamma(\alpha\beta)} &\equiv D=\beta J\sqrt{\beta J_0}(mq-t) \end{align*} 로 간단하게 쓸 수 있다.

상자성 해의 경우 $m=q=t=r=0$이므로 대부분의 성분은 사라지고 대각 성분인 \begin{align*} A&=1-\beta J_0\\ P&=1-\beta^2 J^2 \end{align*} 만이 살아남는다. 복제 대칭해가 안정적이려면 $1-\beta J_0>0$, $1-\beta^2 J^2$를 만족해야 하는데 이 조건은 $T>J_0$, $T>J$와 같다. 위상도표에서도 알 수 있듯이 안정성을 나누는 경계가 상의 경계이므로 상자성 해의 경우엔 복제 대칭해가 항상 안정적이다.

강자성 해의 경우, $m,q\neq0$이므로 다음과 같은 고윳값방정식을 풀어야 한다. $$G\vec\mu = \lambda\vec\mu,\quad \vec\mu = \begin{pmatrix} \{\epsilon^\alpha\}\\ \{\eta^{\alpha\beta}\} \end{pmatrix}$$ 강자성 해가 안정적이려면 이 고윳값 방정식을 통해 얻어낸 $\lambda$가 모두 양수여야 할 것이다.

이 경우는 $\vec\mu_1 = (a,\dots,a,b,\dots,b)$의 꼴로 쓰여지기 때문에 첫 번째 행과 $n+1$번째 행만 살펴보면 된다. $G$의 첫 번째 행은 $$(A,B,\dots,B,C,\dots,C,D,\dots,D)$$ 이고, 이를 $\vec\mu_1$와 곱하면 $$Aa+(n-1)Ba+(n-1)Cb+\frac12(n-1)(n-2)Db=\lambda_1a$$ 가 된다. 마찬가지로 $G$의 $n+1$번째 행은 $$(C,C,D,\dots,D,P,Q,\dots,Q,R,\dots,R)$$ 이고, $\vec\mu_1$와 곱하면 $$2Ca+(n-2)Da+Pb+2(n-2)Qb+\frac12(n-2)(n-3)Rb=\lambda_1b$$ 가 된다. 위 두 식을 연립해서 $\lambda_1$을 구하고 $n\rightarrow0$인 극한을 취해주면 $$\lambda_1 = \frac12\left(A-B+P-4Q+3R\pm\sqrt{(A-B-P+4Q-3R)^2-8(C-D)^2}\right)$$ 를 얻는다.

편의상 $\theta=1$로 두자. 위의 경우와 마찬가지로 첫 번째 행과 $n+1$번째 행을 통해 \begin{align*} Aa+(n-1)Bb+Cc(n-1)+\frac12Dd(n-1)(n-2)&=\lambda_2a\\ aC+bC+(n-2)Db+Pc+(n-2)Qc+(n-2)Qd+\frac12(n-2)(n-3)Rd&=\lambda_2c \end{align*} 임을 알 수 있다. 그리고 고유벡터 $\vec\mu_2$의 $\vec\epsilon_2, \vec\eta_2$는 앞에서 구했던 $\vec\epsilon_1, \vec\eta_1$들과 각각 직교할 것이므로 $\vec\epsilon_1\cdot\vec\epsilon_2=\vec\eta_1\cdot\vec\eta_2=0$인 조건을 통해 $$a+(n-1)b=0,\quad c+\frac12(n-2)d=0$$ 를 만족해야 한다. 이를 대입하고 위 연립방정식을 푼 뒤에 $n\rightarrow0$인 극한을 취해주면 $$\lambda_2 = \frac12\left(A-B+P-4Q+3R\pm\sqrt{(A-B-P+4Q-3R)^2-8(C-D)^2}\right)$$ 를 얻는다. 이는 $\lambda_1$과 동일하다.

이번에도 편의상 $\theta=1$, $\nu=2$로 두자. 먼저 $\vec\mu_1=(x,\dots,x,y,\dots,y)^T$와 $\vec\mu_3$의 직교조건을 이용하면 $$2a+(n-2)b=0,\quad c+2(n-2)d+\frac12(n-2)(n-3)e=0$$ 이고, $\vec\mu_2=(x,y,\dots,y,v,\dots,v,w,\dots,w)^T$와 $\vec\mu_3$의 직교조건을 이용하면 $$ax+ay+(n-2)by=0,\quad cv+(n-2)dv=0,\quad (n-2)dw+\frac12(n-2)(n-3)ew=0$$ 를 얻는데, $\vec\mu_2$의 제약조건 $x+(n-1)y=0$를 적용하면 $$a=b=0,\quad c=(2-n)d,\quad d+\frac12(n-3)e=0$$ 가 되어야 함을 알 수 있다. 따라서 $\vec\mu_3=(0,\dots,0,c,d,\dots,d,e,\dots,e)^T$를 가정하고 고윳값 방정식을 풀면 $$Pc+2(n-2)Qd+\frac12(n-2)(n-3)Re=\lambda_3c$$ 가 되고, $n\rightarrow0$인 극한을 취해주면 $$\lambda_3=P-2Q+R$$ 이 됨을 알 수 있다. 여기서 특정한 복제본 $\theta,\nu$를 선택하는 경우의 수는 $n(n-1)/2$이므로 $\lambda_3$까지만 고려하면 $G$의 차원을 모두 채우게 된다.

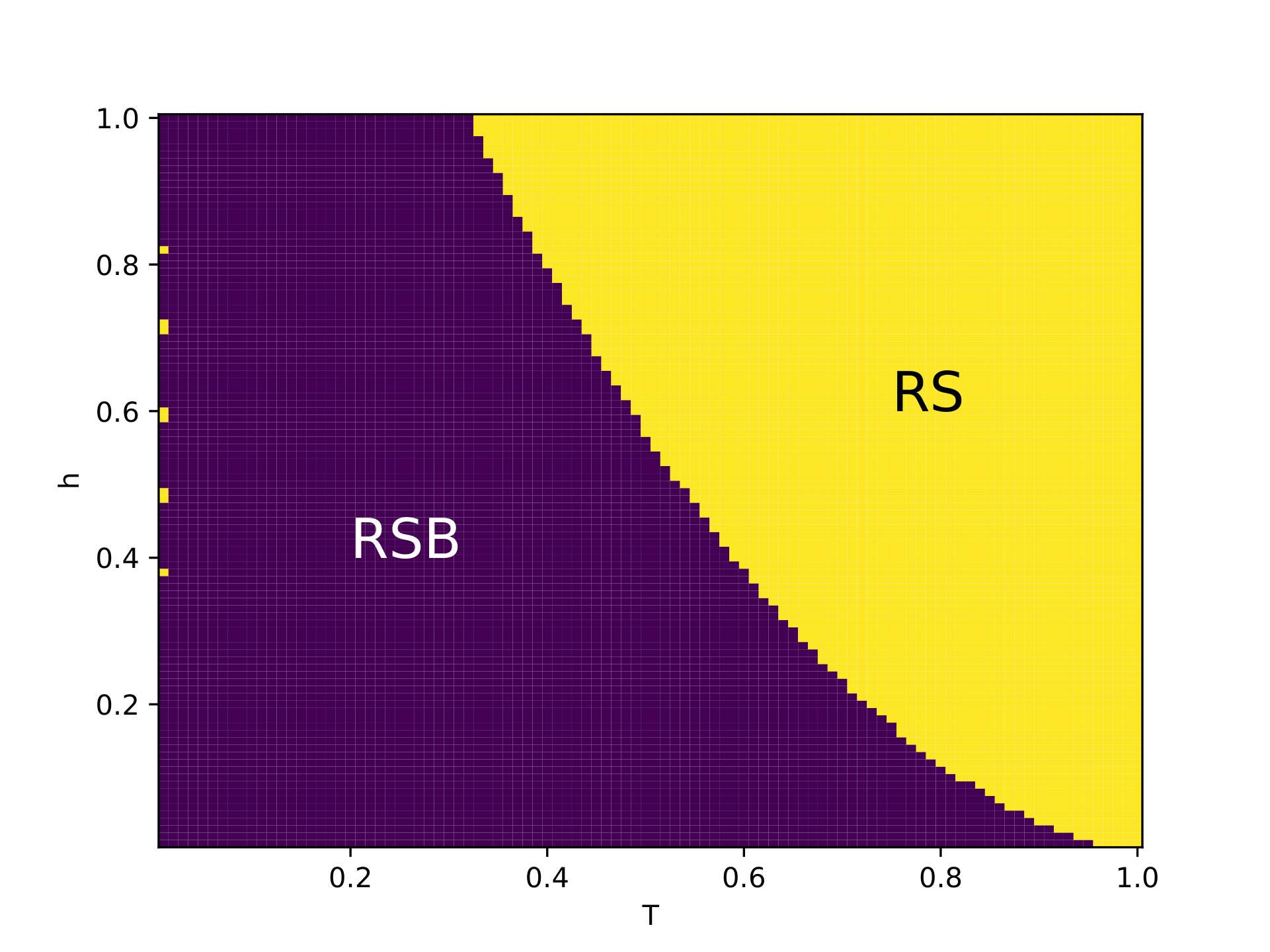
이제 구해낸 두 타입의 고윳값 $\lambda_1=\lambda_2$, $\lambda_3$의 부호를 살펴볼 차례이다. 먼저 $\lambda_{1,2}$가 양수일 충분조건은 $$ A-B = \frac1{J_0}\left.\frac{\partial^2[f]}{\partial m^2}\right\vert_{RS}>0,\quad P-4Q+3R=-\left.\frac2{\beta J^2}\frac{\partial^2[f]}{\partial q^2}\right\vert_{RS}>0 $$ 인데, 이는 복제 대칭해의 자유에너지를 통해 항상 성립함을 볼 수 있다. 반면, $\lambda_3>0$일 충분조건은 $$\left(\frac TJ\right)^2>\int Dz\,\text{sech}^4\left(\beta J\sqrt qz+\beta J_0m\right)$$ 인데 이 조건은 항상 성립하지는 않는다. 예를 들어, $J_0=0$이고 외부 자기장 $h$가 존재할 때 위 식을 수치적으로 풀어보면 복제 대칭해가 안정적인 영역과 그렇지 않은 영역을 구해낼 수 있다.