방금 본 것처럼 복제 대칭성이 있으면 $q_{\alpha\beta} = q$와 $m_{\alpha} = m$로 쓸 수 있다. 헬름홀츠 자유에너지는 \begin{align} -\beta [f] =& -\frac{\beta^2 J^2}{4n} \sum_{\alpha \neq \beta} q_{\alpha \beta}^2 - \frac{\beta J_0}{2n} \sum_{\alpha} m_{\alpha}^2 + \frac{\beta^2 J^2}{4} + \frac{1}{n} \ln \text{Tr}^{\prime} e^L \\ =& -\frac{\beta^2 J^2}{4} \left( n-1 \right) q^2 - \frac{\beta J_0}{2} m^2 + \frac{1}{n} \ln \text{Tr}^{\prime} e^L + \frac{\beta^2 J^2}{4} \end{align} 인데, 대각합 부분을 다음처럼 계산해보자. \begin{align} \text{Tr}^{\prime} e^L =& \text{Tr}^{\prime} \exp \left[ \beta^2 J^2 \sum_{\alpha < \beta} q_{\alpha\beta} S^{\alpha} S^{\beta} + \beta \sum_{\alpha} \left( J_0 m_{\alpha} + h \right) S^{\alpha} \right] \\ =& \text{Tr}^{\prime} \exp \left[ \beta^2 J^2 q \sum_{\alpha < \beta} S^{\alpha} S^{\beta} + \beta \left( J_0 m_{\alpha} + h \right) \sum_{\alpha} S^{\alpha} \right] \\ =& \text{Tr}^{\prime} \exp \left\{ \beta^2 J^2 q \frac{1}{2} \left[ \left( \sum_{i} S_{i}^{\alpha} \right)^2 - n \right] + \beta \left( J_0 m_{\alpha} + h \right) \sum_{\alpha} S^{\alpha} \right\} \\ =& \text{Tr}^{\prime} \sqrt{\frac{\beta^2 J^2 q}{2\pi}} \int_{-\infty}^{\infty} dz \ \exp\left[ -\beta^2 J^2 q \frac{z^2}{2} + \beta^2 J^2 q z \sum_{\alpha} S^{\alpha} - \frac{n}{2} \beta^2 J^2 q + \beta \left( J_0 m + h \right) \sum_{\alpha} S^{\alpha} \right] \end{align} 마지막 줄에서는 $a = \beta^2 J^2 q$, $z = \sqrt{N}m$, 그리고 $x = \sum_{\alpha} S^{\alpha}$인 허바드-스트라토노비치 변환을 사용했다. 대각합은 스핀 변수에 걸리는 것이므로 적분식 안쪽으로 밀어넣고 $\tilde{z} \equiv \beta J \sqrt{q} z$로 정의하자. \begin{align} \text{Tr}^{\prime} e^L =& \sqrt{\frac{\beta^2 J^2 q}{2\pi}} \int_{-\infty}^{\infty} dz \ \exp\left( -\beta^2 J^2 q \frac{z^2}{2} \right) \text{Tr}^{\prime} \exp \left\{ \left[ \beta^2 J^2 q z + \beta \left( J_0 m + h \right) \right] \sum_{\alpha} S^{\alpha} \right\} \exp \left( -\frac{n}{2}\beta^2 J^2 q \right) \\ =& \frac{1}{\sqrt{2\pi}} \int_{-\infty}^{\infty} d\tilde{z} \exp\left( -\frac{\tilde{z}^2}{2} \right) \text{Tr}^{\prime} \exp \left\{ \left[ \beta J \sqrt{q} \tilde{z} + \beta \left( J_0 m + h \right) \right] \sum_{\alpha} S^{\alpha} \right\} \exp \left( -\frac{n}{2}\beta^2 J^2 q \right) \\ =& \int D\tilde{z} \ \left[ 2\cosh \left( \beta J \sqrt{q} \tilde{z} + \beta J_0 m + \beta h \right) \right]^n \exp \left( -\frac{n}{2}\beta^2 J^2 q \right) \end{align} 이 과정에서 \begin{align} \frac{1}{\sqrt{2\pi}} \int_{-\infty}^{\infty} d\tilde{z} \exp\left( -\frac{\tilde{z}^2}{2} \right) \ldots \equiv \int D\tilde{z} \ldots \end{align} 으로 줄여서 적었다 (참고로 $\int D\tilde{z} = 1$). 그리고 $\cosh$ 내부도 간단히 적기 위해 $\tilde{H} (\tilde{z}) \equiv J \sqrt{q} \tilde{z} + J_0 m + h$을 도입한 다음 양변에 자연로그를 취하면, \begin{align} \ln \text{Tr}^{\prime} e^L =& \ln \int D\tilde{z} \exp \left\{ n \ln \left[ 2\cosh \beta \tilde{H} \left( \tilde{z} \right) \right] - \frac{n}{2} \beta^2 J^2 q \right\} \\ \approx& \ln \int D\tilde{z} \left\{ 1+ n \ln \left[ 2\cosh \beta \tilde{H} \left( \tilde{z} \right) \right] - \frac{n}{2} \beta^2 J^2 q \right\} \\ \approx& \ln \left\{ 1+ n \int D\tilde{z} \ln \left[ 2\cosh \beta \tilde{H} \left( \tilde{z} \right) \right] - \frac{n}{2} \beta^2 J^2 q \right\}\\ \underset{n \rightarrow 0}{\longrightarrow}& \ n \left\{ \int D\tilde{z} \ln \left[ 2\cosh \beta \tilde{H} \left(\tilde{z}\right) \right] - \frac{1}{2}\beta^2 J^2 q \right\}. \end{align} 그러므로 \begin{align} \lim_{n \rightarrow 0} \left( -\beta \left[ f \right] \right) =& \frac{\beta^2 J^2}{4}q^2 - \frac{\beta J_0}{2}m^2 + \int D\tilde{z} \ln \left[ 2\cosh \beta \tilde{H} \left(\tilde{z}\right) \right] - \frac{1}{2}\beta^2 J^2 q + \frac{\beta^2 J^2}{4} \\ =& \frac{\beta^2 J^2}{4} \left( q^2 - 2q + 1 \right) - \frac{1}{2} \beta J_0 m^2 + \int D\tilde{z} \ln \left[ 2\cosh \beta \tilde{H} \left(\tilde{z}\right) \right] \\ =& \frac{\beta^2 J^2}{4} \left( 1 - q \right)^2 - \frac{\beta J_0}{2}m^2 + \int D\tilde{z} \ln \left[ 2\cosh \beta \tilde{H} \left(\tilde{z}\right) \right] \end{align} 이다.

자유에너지 범함수를 최소로 하기 위해 미분을 취하면 자기일관성(self-consistency)을 위한 방정식을 얻게 된다. 먼저 $m$에 대해: \begin{equation} 0 = \frac{\partial}{\partial m} \left\{ -\lim_{n \rightarrow 0} \beta \left[ f \right] \right\} = -\beta J_0 m + \frac{\partial}{\partial m} \int D\tilde{z} \ln \left[ 2\cosh\beta\tilde{H}\left(\tilde{z}\right) \right] = -\beta J_0 m + \beta J_0 \int D\tilde{z} \tanh \beta \tilde{H} \left( \tilde{z} \right) \end{equation} \begin{equation} \therefore m = \int D\tilde{z} \tanh \beta \tilde{H}\left(\tilde{z}\right). \end{equation} 다음으로 $q$에 대해: \begin{align} 0 =& \frac{\partial}{\partial q} \left\{ -\lim_{n \rightarrow 0} \beta \left[ f \right] \right\} = \frac{\beta^2 J^2}{2}\left(q-1\right) + \beta J \int D\tilde{z} \tanh \beta \tilde{H}\left(\tilde{z}\right) \frac{\tilde{z}}{2\sqrt{q}} \\ =& \frac{\beta^2 J^2}{2}\left(q-1\right) + \frac{\beta J}{2\sqrt{q}} \int D\tilde{z} \ \tilde{z} \tanh \beta\tilde{H}\left(\tilde{z}\right) \end{align} 그런데 여기에서 마지막의 항을 부분적분하면 더 간단히 적을 수 있다: \begin{align} \int D\tilde{z} \ \tilde{z} \tanh \beta\tilde{H}\left(\tilde{z}\right) =& \frac{1}{\sqrt{2\pi}} \int d\tilde{z} \exp \left( -\frac{\tilde{z}^2}{2} \right) \tilde{z} \tanh \left(\beta J \sqrt{q} \tilde{z}\right) \\ =& - \frac{1}{\sqrt{2\pi}} \left[ \exp \left( -\frac{\tilde{z}^2}{2} \right) \tanh \left( \beta J \sqrt{q} \tilde{z} \right) \right]_{-\infty}^{\infty} + \frac{1}{\sqrt{2\pi}} \int d\tilde{z} \exp \left( -\frac{\tilde{z}^2}{2} \right) \beta J \sqrt{q} \ \text{sech}^2 \left( \beta J \sqrt{q} \tilde{z} \right) \\ =& \int D\tilde{z} \ \beta J \sqrt{q} \ \text{sech}^2 \left( \beta J \sqrt{q} \tilde{z} \right) \end{align} 이를 위의 식에 대입하면 \begin{equation} \frac{\beta^2 J^2}{2} \left(q-1\right) + \frac{\beta^2 J^2}{2} \int D\tilde{z} \ \text{sech}^2 \tilde{H} \left( \tilde{z} \right)=0 \end{equation} 이고 이 식을 정리하면 \begin{equation} q = 1 - \int D\tilde{z} \ \text{sech}^2 \tilde{H} \left( \tilde{z} \right) = \int D \tilde{z} \tanh^2 \beta \tilde{H} \left( \tilde{z} \right). \end{equation}

외부 자기장이 $h=0$이고 $J_{ij}$의 평균이 $J_0=0$인 상황을 고려하자. 그러면 \begin{equation} \tilde{H} \left( \tilde{z} \right) = J \sqrt{q} \tilde{z} \end{equation} 이 홀함수이기 때문에 $m = \int D\tilde{z} \ \tanh \beta J \sqrt{q} \tilde{z} = 0$이다. 이 결과를 자유에너지에 다시 대입하고 $\cosh$와 $\ln$을 급수전개하면: \begin{align} -\beta \left[ f \right] =& \frac{1}{4} \beta^2 J^2 \left( 1-q \right)^2 + \int D\tilde{z} \ \ln\left[ 2\cosh \left( \beta J \sqrt{q} \tilde{z} \right) \right] \\ \approx& \frac{1}{4} \beta^2 J^2 \left( 1-q \right)^2 + \ln 2 + \int D\tilde{z} \ln \left[ 1 + \frac{1}{2}\beta^2 J^2 q \tilde{z}^2 + \frac{1}{24}\beta^4 J^4 q^2 \tilde{z}^4 \right] \qquad \left( q \ll 1 \right) \\ \approx& \frac{1}{4} \beta^2 J^2 \left( 1-q \right)^2 + \ln 2 + \int D\tilde{z} \left( \frac{1}{2}\beta^2 J^2 q \tilde{z}^2 + \frac{1}{24}\beta^4 J^4 q^2 \tilde{z}^4 - \frac{1}{8}\beta^4 J^4 q^2 \tilde{z}^4 \right) \\ =& \frac{1}{4} \beta^2 J^2 + \ln 2 + \frac{1}{2}\beta^2 J^2 q - \frac{1}{4} \beta^4 J^4 q^2 \\ =& \frac{1}{4} \beta^2 J^2 + \ln 2 + \frac{1}{4}\beta^2 J^2 \left( 1 - \beta^2 J^2 \right)q^2. \end{align} 따라서 \begin{equation} \beta\left[ f \right] \cong -\frac{1}{4} \beta^2 J^2 - \ln 2 -\frac{1}{4}\beta^2 J^2 \left( 1 - \beta^2 J^2 \right)q^2 \end{equation} 이므로, 스핀유리 상전이는 $T = T_f \equiv J/k_B$에서 일어난다. 문제는 온도 $T$가 $T_f$보다 높아질 때 $q^2$ 앞의 계수가 음수가 되므로 마치 온도가 높아질 때에 스핀유리 상이 나타나는 듯이 보인다는 점이다. 이는 $n\to 0$을 취하는 이 방법의 문제점으로, 위에서 '자유에너지 범함수'의 부분을 보면 $n<1$일 때 $q^2$ 앞의 계수가 부호를 바꾸는 것을 볼 수 있다.

이제 $J_0 > 0$이면 $m$이 0이 아닌 값을 취할 수 있게 된다. 위에 적었던 방정식을 전개해서 $q$와 $m$의 가장 낮은 차수 항만을 남기면 $\tanh^2 x \approx x^2$이므로 \begin{align} q =& \int D\tilde{z} \ \tanh^2 \left( \beta J \sqrt{q} \tilde{z} + \beta J_0 m \right) \\ \approx& \int D\tilde{z} \left( \beta^2 J^2 q \tilde{z}^2 + 2\beta^2 J J_0 \sqrt{q} m\tilde{z} + \beta^2 J_0^2 m^2 \right) \\ =& \beta^2 J_0^2 m^2 + \beta^2 J^2 q. \end{align} 위의 식은 만일 $0<m \ll 1$이라면 $q \sim \mathcal{O}(m^2)$일 것임을 의미한다. 이제 $m$에 대한 방정식을 보면, \begin{align} m =& \int D\tilde{z} \ \tanh \left( \beta J \sqrt{q} \tilde{z} + \beta J_0 m \right) \\ \approx& \int D\tilde{z} \left( \beta J \sqrt{q} \tilde{z} + \beta J_0 m \right) \end{align} 인데 $\sqrt{q} \sim \mathcal{O}(m)$에 비례하는 부분은 적분에 의해 사라지고 적분 밖으로 빠져나오는 $q$ 의존성은 $\mathcal{O}(m)$에 비해 작을 것이다. 따라서 $m \approx \beta J_0 m$에서 상전이가 일어난다고 보아도 되며 이는 강자성 임계점이 $T_c = J_0/k_B$임을 뜻한다.

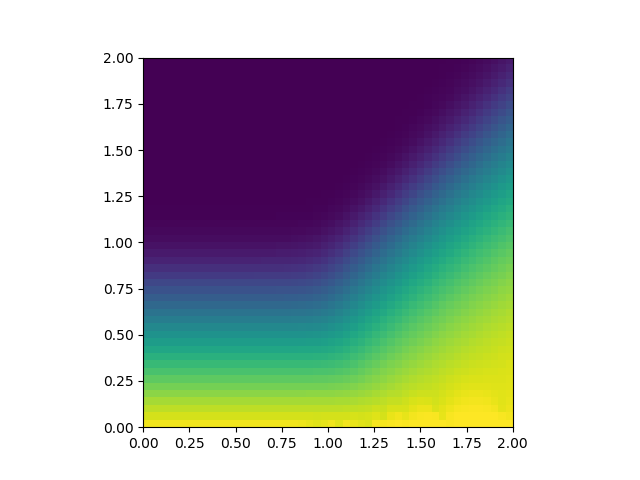
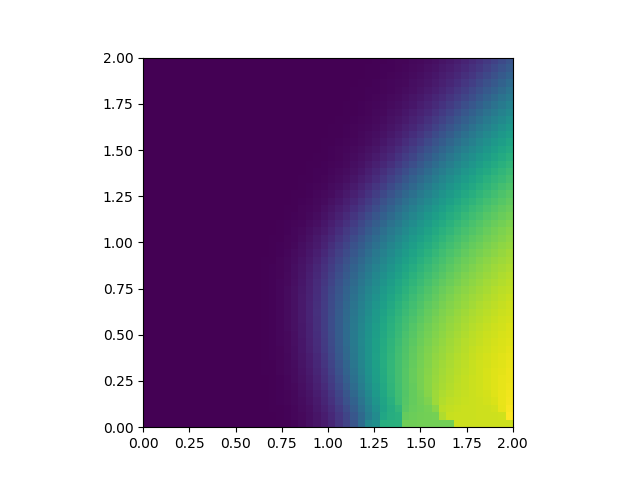
스핀유리와 강자성 사이의 경계는 앞의 식들을 수치적으로 풂으로써 찾을 수 있다. 아래 두 그림에서 가로축은 $J_0/J$, 세로축은 $k_B T/J$를 나타낸다. 첫 번째 그림은 $q$, 두 번째 그림은 $m$의 값을 나타내며, 밝을수록 1에 가깝다. 스핀유리상은 왼쪽 아래($q>0$, $m=0$)이며 강자성상은 오른쪽 아래($q>0$, $m>0$), 상자성상은 윗부분($q=m=0$)이다. 스핀유리상이 $J_0>J$인 영역까지도 조금 침범하고 있음을 볼 수 있다. 그러나 사실 이 영역은 복제대칭성 깨짐을 도입하면 사라진다.

$T \rightarrow 0$에서 $q = 1 - aT$처럼 쓸 수 있다고 가정하자. \begin{align} q =& 1 - \int D\tilde{z} \ \text{sech}^2 \beta J \sqrt{q} \tilde{z} \approx 1 - \int D\tilde{z} \ \text{sech}^2 \beta J \tilde{z} = 1 - \frac{1}{\beta J} \int D\tilde{z} \ \frac{d}{d\tilde{z}} \tanh \beta J \tilde{z} \\ \underset{\beta \rightarrow \infty}{\longrightarrow} & 1 - \frac{1}{\beta J} \int D\tilde{z} \ 2\delta\left( \tilde{z} \right) = 1 - \frac{1}{\beta J} \frac{1}{\sqrt{2\pi}} 2 = 1 - \sqrt{\frac{2}{\pi}} \cdot \frac{k_B}{J} \cdot T \end{align} 이므로 앞의 가정과 일치하려면 $a = k_B\sqrt{2/\pi}/J$임을 알 수 있다.

$J_0 = 0$인 경우 자유에너지 표현식에 위 결과를 대입해보자: \begin{align} -\beta \left[ f \right] =& \frac{1}{4} \beta^2 J^2 \left( 1-q \right)^2 + \int D\tilde{z} \ \ln\left[ 2\cosh \left( \beta J \sqrt{q} \tilde{z} \right) \right] \\ \approx& \frac{1}{4}\beta^2 J^2 \frac{2}{\pi} \frac{1}{\beta^2 J^2} + 2 \int_0^{\infty} D\tilde{z} \ \ln\left[ \exp\left( \beta J \sqrt{q} \tilde{z} \right) + \exp\left( - \beta J \sqrt{q} \tilde{z} \right) \right] \\ =& \frac{1}{2\pi} + 2\int_0^{\infty} D\tilde{z} \ \ln \left\{ \exp \left( \beta J \sqrt{q} \tilde{z} \right) \left[ 1 + \exp \left( -2\beta J \sqrt{q} \tilde{z} \right) \right] \right\} \\ =& \frac{1}{2\pi} + 2\int_0^{\infty} D\tilde{z} \ \left[ \beta J \sqrt{q} \tilde{z} + \ln \left( 1 + e^{-2\beta J \sqrt{q} \tilde{z}} \right) \right] \\ \approx& \frac{1}{2\pi} + \sqrt{\frac{2}{\pi}}\beta J \sqrt{q} + 2 \int_0^{\infty} D\tilde{z} \ e^{-2\beta J \sqrt{q} \tilde{z}} \end{align} 뒤의 적분항은 $\beta \gg 1$ 인 경우 무시할 수 있으므로 \begin{align} \therefore \ -\beta \left[ f \right] \approx& \frac{1}{2\pi} + \sqrt{\frac{2}{\pi}}\beta J \left( 1 - \frac{1}{2}\sqrt{\frac{2}{\pi}}\frac{1}{\beta J} \right) \\ =& \frac{1}{2\pi} + \sqrt{\frac{2}{\pi}}\beta J - \frac{1}{2} \cdot \frac{2}{\pi} = -\frac{1}{2\pi} + \sqrt{\frac{2}{\pi}}\beta J \end{align} 양변에 $\beta$를 곱하면 \begin{equation} \left[ f \right] \approx \frac{k_B T}{2\pi} - \sqrt{\frac{2}{\pi}}J \end{equation} 인데, 이를 $E-TS$라는 자유에너지 표현식과 비교하면 바닥상태의 에너지가 $-\sqrt{2/\pi}J \approx -0.8J$이며 그때 엔트로피가 $-k_B/(2\pi) \approx -0.16k_B$임을 유추할 수 있다. 엔트로피가 음수라고 하는 이 이상한 거동은 파리시(G. Parisi)가 복제 대칭성 깨짐(replica symmetry breaking)을 도입함으로써 해결했다.