사다리(ladder) 위의 이징 모형

$2 \times M$ 사각 격자 상의 2차원 이징 모형을 다음과 같은 해밀토니안 $H$로 기술하자

$$ -\beta H = K \sum_{n=1}^2 \sum_{m=1}^M \left(S_{m,n}S_{m+1,n} + S_{m,n}S_{m,n+1} \right) $$

이때, 주기적 경계 조건(periodic boundary condition)을 양 방향에 적용하여 $S_{M+1,n}\equiv S_{1,n}$과 $S_{m,3}\equiv S_{m,1}$이 성립하도록 설정하여 설명하겠다.

$$ \\ $$

위의 해밀토니안을 이용해 분배 함수(partition function)를 구한다면 그 계에 대한 해석이 가능할 것이다.

$$ \\ $$ 분배 함수를 원활히 구하기 위해서는, 그를 등가적으로 표현하는 '전달 행렬 (transfer matrix)'의 각 성분을 구하고

그의 고유값을 얻는 방법을 사용할 수 있다. 따라서, 아래의 분배 함수를

$$ Z= \sum_{\{S_{m,n}\}} e^{-\beta H} $$

전달 행렬을 이용한 표현식으로 적절히 바꾸고자 한다.

위에서 주어진 해밀토니안을 이용하여 분배 함수를 다음과 같이 표현할 수 있다.

$$ Z= \sum_{\{S_{m,n}\}} e^{-\beta H} = \sum_{\{S_{m,n}\}} \exp \left[ K \sum_{n=1}^2 \sum_{m=1}^M \left(S_{m,n}S_{m+1,n} + S_{m,n}S_{m,n+1} \right) \right] \\ = \sum_{\{S_{m}\}} \exp \left[ K \sum_{m=1}^M \left(S_{m,1}S_{m+1,1} + S_{m,2}S_{m+1,2} + 2S_{m,1}S_{m,2} \right) \right] \\ = \sum_{\{S_{m}\}} \exp \left[ K \sum_{m=1}^M \left(S_{m,1}S_{m+1,1} + S_{m,2}S_{m+1,2} + S_{m,1}S_{m,2} + S_{m+1,1}S_{m+1,2} \right) \right] \\ = \sum_{\{S_{m}\}} \prod_{m=1}^M \exp \left[ K \left(S_{m,1}S_{m+1,1} + S_{m,2}S_{m+1,2} + S_{m,1}S_{m,2} + S_{m+1,1}S_{m+1,2} \right) \right] $$

$$ \\ $$ 위 식의 두번째 줄에서 $2S_{m,1}S_{m,2}$를 ($m=1$ 부터 $m=M$ 까지의 합에 대해 주기적 경계 조건을 적용하여) 세번째 줄의 $S_{m,1}S_{m,2} + S_{m+1,1}S_{m+1,2}$로 바꾸어 쓸 수 있다.

또한, $\exp$ 함수의 수학적인 특성을 이용하면 지수의 합을 $\exp$ 함수들의 곱으로 대체하여 마지막 줄로 쓸 수 있다.

$$ \\ $$ 여기서 우리는 '전달 행렬' $T_{mn}$를 이용하여 분배 함수 $Z$를 행렬 간의 곱 형태로 나타내고 싶다.

따라서, 아래와 같이 전달 행렬의 성분을 정의하자.

$$ T_{mn}(S_{m,1},S_{m,2},S_{n,1},S_{n,2}) \equiv \exp\left[K \left(S_{m,1}S_{n,1} + S_{m,2}S_{n,2} + S_{m,1}S_{m,2} + S_{n,1}S_{n,2} \right) \right] $$

$$ \\ $$ 각각의 스핀($S$) 값에 대해 그러한 성분을 갖는 전달 행렬을 전체적으로 다음과 같이 표현할 수 있다.

$$ \boldsymbol{T}_{mn} \equiv \begin{pmatrix} T_{mn}(1,1,1,1) & T_{mn}(1,1,1,-1) & T_{mn}(1,1,-1,1) & T_{mn}(1,1,-1,-1) \\ T_{mn}(1,-1,1,1) & T_{mn}(1,-1,1,-1) & T_{mn}(1,-1,-1,1) & T_{mn}(1,-1,-1,-1) \\ T_{mn}(-1,1,1,1) & T_{mn}(-1,1,1,-1) & T_{mn}(-1,1,-1,1) & T_{mn}(-1,1,-1,-1) \\ T_{mn}(-1,-1,1,1) & T_{mn}(-1,-1,1,-1) & T_{mn}(-1,-1,-1,1) & T_{mn}(-1,-1,-1,-1) \end{pmatrix} $$

이러한 전달 행렬을 이용해서 분배 함수 $Z$를 다음과 같이 표현하자.

$$ Z= \sum_{\{S_{m}\}} \prod_{m=1}^M \exp \left[ K \left(S_{m,1}S_{m+1,1} + S_{m,2}S_{m+1,2} + S_{m,1}S_{m,2} + S_{m+1,1}S_{m+1,2} \right) \right] \\ = \sum_{\{S_{m}\}} \prod_{m=1}^M T_{m,m+1}(S_{m,1},S_{m,2},S_{m+1,1},S_{m+1,2}) \\ = Tr\left(\boldsymbol{T}_{12}\boldsymbol{T}_{23} ... \boldsymbol{T}_{M-1,M}\boldsymbol{T}_{M,M+1} \right) \\ = Tr\left(\boldsymbol{T}^M \right)$$

위의 식 두번째 줄에서 세번째 줄로 넘어갈 때, 대각 성분들의 합(trace, $Tr$)을 계산하는 것으로서 등식이 성립함을 이용하였으며

그러한 관계가 성립하는 이유를 간단히 소개하자면 다음과 같다.

앞서 보았던 아래의 식에서

$$ Z= \sum_{\{S_{m}\}} \prod_{m=1}^M \exp \left[ K \left(S_{m,1}S_{m+1,1} + S_{m,2}S_{m+1,2} + S_{m,1}S_{m,2} + S_{m+1,1}S_{m+1,2} \right) \right] \\ = \sum_{\{S_{m}\}} \prod_{m=1}^M T_{m,m+1}(S_{m,1},S_{m,2},S_{m+1,1},S_{m+1,2}) $$

$ \sum_{\{S_{m}\}} $은 임의의 위치(site)인 $(m,m+1)$ 스핀에 대해서 합을 계산한다는 의미이다.

즉, $ \sum_{\{S_{m}\}} $를 $ \sum_{\{S_{1}\}}\sum_{\{S_{2}\}}\sum_{\{S_{3}\}} \ ... \ \sum_{\{S_{M}\}} $으로 표현한다면 다음의 과정을 통해 대각합의 결과를 이해할 수 있다.

$$ \\ $$

우선, $\sum_{\{S_{m}\}}$의 $m$ 중에서 $m=2$와 관련된 부분 부터 고려하는 다음의 식을

행렬 곱의 표기법을 적용해서 풀이해보자.

$$ \sum_{\{S_{1}\}} \sum_{\{S_{2}\}} T_{12}T_{23} = \sum_{\{S_{1}\}} T^2_{13} $$

$$ \\ $$ 이어서, $m=3$과 관련된 부분도 고려하여 다음과 같이 풀이해보자.

$$ \sum_{\{S_{1}\}} \sum_{\{S_{3}\}} T_{13}^2 T_{34} = \sum_{\{S_{1}\}} T^3_{14} $$

$$ \\ $$ 이러한 방식대로 $m=M$인 합 계산( $\sum $ )까지 진행하면, 주기적 경계 조건에 따라서 다음을 얻게 된다.

$$ \sum_{\{S_{1}\}} \sum_{\{S_{M}\}} T_{1,M}^{M-1} \ T_{M,M+1} = \sum_{\{S_{1}\}} \sum_{\{S_{M}\}} T^{M-1}_{1,M} \ T_{M,1} = \sum_{\{S_{1}\}} T^{M}_{1,1} $$

이때, 위 식의 마지막 결과에서 $T^M _{1,1}$을 ${S_1}$에 대하여 합해주는 것은 $\boldsymbol{T^M}$의 대각합을 구하는 것이므로 $Tr\left( \boldsymbol{T^M} \right) $과 같다.

$$ \\ $$

앞서 언급된 전달 행렬 정의의 수식을 이용해서

$$ T_{m,m+1}(S_{m,1},S_{m,2},S_{m+1,1},S_{m+1,2}) \equiv \exp\left[K \left(S_{m,1}S_{m+1,1} + S_{m,2}S_{m+1,2} + S_{m,1}S_{m,2} + S_{n,1}S_{m+1,2} \right) \right] $$

행렬의 각 성분에 대입해주면 다음과 같다.

$$ \boldsymbol{T}_{m,m+1} = \begin{pmatrix} e^{4K} & 1 & 1 & 1 \\ 1 & 1 & e^{-4K} & 1 \\ 1 & e^{-4K} & 1 & 1 \\ 1 & 1 & 1 & e^{4K} \end{pmatrix} \equiv \boldsymbol{T} $$

$$ \\ $$ 앞서 우리는 $ Z = Tr\left(\boldsymbol{T}^M \right)$의 결과를 얻었으므로, $\boldsymbol{T}$를

대각 성분만을 갖는 대각 행렬 $\boldsymbol{D}$에 대해 $\boldsymbol{T} = \boldsymbol{UDU^{-1}}$ 으로 '대각선화(대각화, diagonalization)' 해준다면

$ \boldsymbol{T}^M = \boldsymbol{U D^M U^{-1}} $이 성립한다. ($\because \boldsymbol{UU^{-1}} = \boldsymbol{U^{-1}U} = \boldsymbol{E} $, $\boldsymbol{E}$ : 단위 행렬)

$$ \\ $$ 이때, 다음과 같은 대각합의 성질에 따르면

$Tr(\boldsymbol{ABC})=Tr(\boldsymbol{BCA})=Tr(\boldsymbol{CAB})$

다음의 관계가 성립한다.

$ Tr(\boldsymbol{T}^M) = Tr(\boldsymbol{U D^M U^{-1}}) = Tr(\boldsymbol{D^M U^{-1} U}) = Tr(\boldsymbol{D^M}) $

$$ \\ $$ 즉, 대각 성분만을 갖는 행렬 $\boldsymbol{D}$를 $M$번 거듭 곱셈한 결과는 $\boldsymbol{D}$의 각 대각 성분들에 $M$ 거듭 제곱을 취해준 것과 같다는 성질을 이용하여

$\boldsymbol{D^M}$을 구하면 보다 쉽게 대각합을 구할 수 있다.

$$ \\ $$ 분배 함수 $Z$를 구하기 위한 행렬 $\boldsymbol{D}$는 (Mathematica 등의 프로그램 등을 이용하여) 다음과 같이 얻을 수 있으며

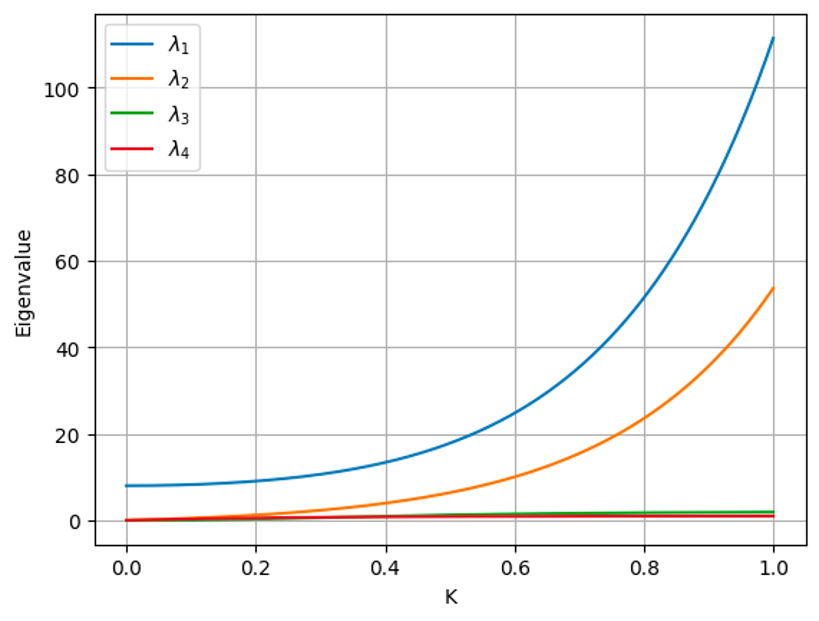
크기가 큰 순서대로 고유값을 나열하면 다음과 같다.

$$ \lambda_1 = \frac{1}{2} e^{-4K}(1+2e^{4K}+e^{8K}+\sqrt{1+14e^{8K}+e^{16K}}), \ \lambda_2 = -1+e^{4K}, \\ \lambda_3 = \frac{1}{2} e^{-4K}(1+2e^{4K}+e^{8K}-\sqrt{1+14e^{8K}+e^{16K}}), \ \lambda_4 = 1-e^{-4K} $$

$\boldsymbol{D}$의 대각 성분들을 구했으므로, $Z =Tr(\boldsymbol{T^M}) =Tr(\boldsymbol{D^M})$의 식을 이용하여

$$ Z = Tr\left(\boldsymbol{T}^M \right) = \lambda_1^M + \lambda_2^M + \lambda_3^M + \lambda_4^M $$

위와 같이 분배 함수 $Z$를 구할 수 있다.

$$ \\ $$

$K$의 값이 큰 경우에는, 이러한 4가지 값 중에서 (아래와 같이) 가장 크기가 큰 $\lambda_1$과 $\lambda_2$가 $Z$ 값의 대부분을 차지하므로

다음과 같이 나타낼 수 있다.

$$ Z = Tr\left(\boldsymbol{T}^M \right) = \lambda_1^M + \lambda_2^M + \lambda_3^M + \lambda_4^M \approx \lambda_1^M + \lambda_2^M $$

$$ \\ $$

Gun Sang Jeon, Fundamentals of Quantum Phase Transitions, 2023.

Seung Ki Baek and Harri M¨akel¨a, Internal energy density of the critical three-state Potts model on the kagome lattice, 2013.