단일 입자 양자역학을 통해서 '빛 보다 더 빠르게 움직이는 입자의 진폭(amplitude)'를 구해보고자 한다.

상대성이론에 따라서 빛 보다 빠르게 움직일 수 있는 것은 없다. 그렇다면 그 진폭은 $0$이어야 할 것인데, 실제로 그러한지 확인해고자 한다.

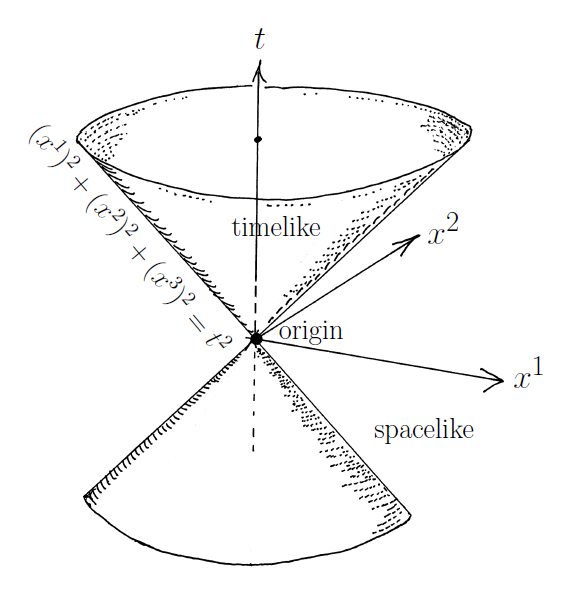
$$ \\ $$ 우선 '빛 보다 빠른 입자'를 '빛원뿔(light cone)'위에서 더 쉽게 이해할 수 있다.

즉, 특수상대성 이론에 위배되지 않는 (허용되는) 경로(time-like라고 부른다)는 원뿔의 안쪽에 해당하며 다음을 만족하는 것이다.

$$ |x|^2 =t^2-(x^1)^2-(x^2)^2-(x^3)^2 >0 $$

광자(photon)의 경우는 $ |x|^2 =t^2-(x^1)^2-(x^2)^2-(x^3)^2 =0 $ 으로서, 원뿔면 위에 놓이는 경로를 따라 간다.

$$ \\ $$ 이때, $ |x|^2 =t^2-(x^1)^2-(x^2)^2-(x^3)^2 <0 $의 경로(space-like라고 부른다)를 따라가는 경로는 허용가능하지 않는 것이다.

그럼 해당 경로에 대해서, 다음과 같은 양을 정의하고

$$ \mathcal{A}=\langle \boldsymbol{x} |e^{-i\hat{H}t}| \boldsymbol{x}=0\rangle $$

$$ \begin{align} \mathcal{A}=\langle \boldsymbol{x} |e^{-i\hat{H}t}| \boldsymbol{x}=0\rangle &= \int d^3p \langle \boldsymbol{x} |e^{-i\hat{H}t}|\boldsymbol{p}\rangle \langle \boldsymbol{p}|\boldsymbol{x}=0 \rangle \\ &= \int d^3p \langle \boldsymbol{x} | \boldsymbol{p} \rangle e^{-iE_pt} \frac{1}{(2\pi)^{3/2}}e^{-i\boldsymbol{p}\cdot 0} \\ &= \int d^3p \frac{1}{(2\pi)^3}e^{i\boldsymbol{p}\cdot \boldsymbol{x}}e^{-iE_p t}. \end{align} $$ $| \mathcal{A}| ^2$이 0이 아닌지를 확인해보자.

$$ \\ $$ 첫 번째 줄에서는 완전 집합(complete set)의 성질인 $1=\int d^ep | \boldsymbol{p} \rangle \langle \boldsymbol{p}| $을 이용하였다.

두 번째 줄로 넘어갈 때, $e^{-i\hat{H}t}$를 $|\boldsymbol{p}\rangle$에 걸어줌으로써 고유값을 $e^{-iE_pt}$로 얻었다. 또한, 다음의 식을 이용하였다.

$$ \langle \boldsymbol{x} | \boldsymbol{p}\rangle =\frac{1}{(2\pi)^{3/2}}e^{i\boldsymbol{p}\cdot \boldsymbol{x}} $$ (규격화 상수(normalization constant)가 정확한 값일 필요는 없다. $\mathcal{A}$가 0인지, 그렇지 않은지만 파악하면 되기 때문이다.)

이제 해야할 것은, 다음의 적분 계산을 $ |x|^2 =t^2-(x^1)^2-(x^2)^2-(x^3)^2 <0 $ (space-like) 에 해당하는 간격(interval)에 대해서 풀이하는 것이다.

$$ \begin{align} \mathcal{A}=\int d^3p \frac{1}{(2\pi)^3}e^{i\boldsymbol{p}\cdot \boldsymbol{x}}e^{-iE_p t}. \end{align} $$ 이러한 적분식을 구면 좌표계 (spherical polars)로 다음과 같이 변환하자. $$ \begin{align} \mathcal{A} &= \int _0 ^{2\pi} d\phi \int^\infty _0 \frac{d|\boldsymbol{p} |}{(2\pi)^3}|\boldsymbol{p}|^2 \int^{\pi} _{0} d\theta e^{i\boldsymbol{p}\cdot \boldsymbol{x}}e^{-iE_p t} \\ &= \int _0 ^{2\pi} d\phi \int^\infty _0 \frac{d|\boldsymbol{p} |}{(2\pi)^3}|\boldsymbol{p}|^2 \int^{-1} _{1} (-du) e^{i|\boldsymbol{p}||\boldsymbol{x}|u}e^{-iE_p t} \\ &= \frac{1}{{(2\pi)^3}}\int _0 ^{2\pi} d\phi \int^\infty _0 d|\boldsymbol{p} |\ |\boldsymbol{p}|^2 \int^{1} _{-1} du e^{i|\boldsymbol{p}||\boldsymbol{x}|u}e^{-iE_p t} \\ &= \frac{1}{(2\pi)^3}(2\pi)\int^\infty _0 d|\boldsymbol{p} |\ |\boldsymbol{p}|^2 \left( \frac{1}{i(|\boldsymbol{p}||\boldsymbol{x}|)} \right)\left[e^{i|\boldsymbol{p}||\boldsymbol{x}|u}\right]_{-1}^{1}\ e^{-iE_p t} \\ &= \frac{-i}{(2\pi)^2|\boldsymbol{x}|}\int^\infty _0 d|\boldsymbol{p} |\ |\boldsymbol{p}| \left[e^{i|\boldsymbol{p}||\boldsymbol{x}|}-e^{-i|\boldsymbol{p}||\boldsymbol{x}|}\right] \ e^{-iE_p t} \\ \end{align} $$ 위의 식을 풀이할 때, $\cos\theta \equiv u \to -du=\sin\theta d\theta$를 이용하였다.

구면 좌표계의 야코비안(Jacobian)이 $r^2 \sin\theta $임을 참고하자.

$$ \\ $$ (참고로, 위의 계산에서 아직 $ |x|^2 =t^2-(x^1)^2-(x^2)^2-(x^3)^2 <0 $라는 조건은 대입하지 않았다.) $$ \\ $$ 위에서 마지막 줄의 적분식을 두 항으로 분리한 뒤, 적분 범위를 아래와 같이 바꿔주면 보다 간단해진다.

$$ \begin{align} \mathcal{A} &= \frac{-i}{(2\pi)^2|\boldsymbol{x}|}\int^\infty _0 d|\boldsymbol{p} |\ |\boldsymbol{p}| \left[e^{i|\boldsymbol{p}||\boldsymbol{x}|}-e^{-i|\boldsymbol{p}||\boldsymbol{x}|}\right] \ e^{-iE_p t} \\ &= \frac{-i}{(2\pi)^2|\boldsymbol{x}|}\left(\int^\infty _0 d|\boldsymbol{p} |\ |\boldsymbol{p}| e^{i|\boldsymbol{p}||\boldsymbol{x}|} \ e^{-iE_p t} - \int^\infty _0 d|\boldsymbol{p} |\ |\boldsymbol{p}| e^{-i|\boldsymbol{p}||\boldsymbol{x}|} \ e^{-iE_p t}\right) \\ &= \frac{-i}{(2\pi)^2|\boldsymbol{x}|}\left(\int^\infty _0 d|\boldsymbol{p} |\ |\boldsymbol{p}| e^{i|\boldsymbol{p}||\boldsymbol{x}|} \ e^{-iE_p t} - \int^{-\infty }_0 (d(-|\boldsymbol{p} |)\ (-|\boldsymbol{p}|) e^{i|\boldsymbol{p}||\boldsymbol{x}|} \ e^{-iE_p t}\right) \\ &= \frac{-i}{(2\pi)^2|\boldsymbol{x}|}\left(\int^\infty _0 d|\boldsymbol{p} |\ |\boldsymbol{p}| e^{i|\boldsymbol{p}||\boldsymbol{x}|} \ e^{-iE_p t} + \int^{0}_{-\infty } d|\boldsymbol{p} |\ |\boldsymbol{p}| e^{i|\boldsymbol{p}||\boldsymbol{x}|} \ e^{-iE_p t}\right) \\ &= \frac{-i}{(2\pi)^2|\boldsymbol{x}|}\left(\int^\infty _{-\infty } d|\boldsymbol{p} |\ |\boldsymbol{p}| e^{i|\boldsymbol{p}||\boldsymbol{x}|} \ e^{-it\sqrt{|\boldsymbol{p}|^2 + m^2}} \right) \\ \end{align} $$ 두 번째 줄에서 세 번째 줄로 넘어갈 때, $|p|$에 대한 적분을 $-|p|$에 대한 것으로 바꿔주었다.

또한, $E_p = \sqrt{|\boldsymbol{p}|^2 + m^2}$을 대입하였다.

$$\\$$ 위의 적분을 풀이하는 수학적인 방법은 복소(complex) 적분이다.

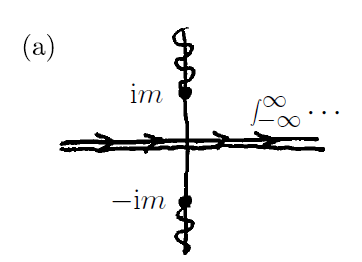
우리가 계산하고자 하는 적분은 $|\boldsymbol{p}|$의 $-\infty$ 부터 $\infty$까지의 범위에 대한 적분이므로

복소평면에서 아래와 같은 경로를 따라서 다음의 적분을 계산해야 한다.

$$ \mathcal{A} = \frac{-i}{(2\pi)^2|\boldsymbol{x}|}\left(\int^\infty _{-\infty } d|\boldsymbol{p} |\ |\boldsymbol{p}| e^{i|\boldsymbol{p}||\boldsymbol{x}|} \ e^{-it\sqrt{|\boldsymbol{p}|^2 + m^2}} \right) \\ $$

(허수축이 $\pm im$에서 잘린(cut) 이유는, 시간 연산자(time operator)의 고유값에 해당하는 $e^{-iE_pt}$의 지수는 허수이기 때문이다.

$$ \\ $$ 이때, '코시의 정리(Cauchy's theorem)'를 이용한다면 적분을 보다 원활하게 풀이할 수 있다.

'코시의 정리'란, 임의의 복소수 $z$에 대한 함수 $f(z)$가 경로 $C$와 그 내부에서 해석적(anaylytic)일 때, 다음의 식을 만족한다는 것이다.

$$ \oint_C dz\ f(z) = 0. $$

즉, 경로 $C$ 내부에서 적분되는 함수 $f(z)$가 해석적이지 않은 특이점이 포함되지 않는다면

해당 적분은 시작점과 종점에만 의존한다.

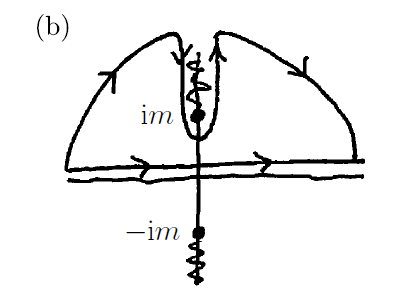
$$ \\ $$ 이때, 다음의 그림의 닫힌 곡선 안에서는 특이점이 존재하지 않는다.

따라서 우리의 적분을 반원 위쪽을 지나는 경로에 대한 적분으로 바꾸는 것이 가능하다.

$$ \\ $$ 또한, '조르당의 보조 정리(Jordan’s lemma)'에 따르면, 반원의 크기가 커질수록

반원을 지나는 적분의 (총 적분에 대한) 기여분은 $0$에 근접한다.

('조르당의 보조 정리'는 이번 게시글 맨 아래에 보충 설명하였다.)

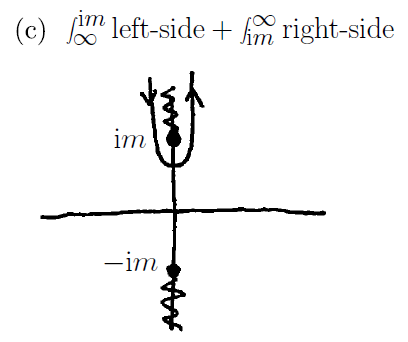
$$ \\ $$ 따라서, 유의미한 적분 경로는 아래의 그림과 같다.

$$ \\ $$

조르당의 보조 정리란,

$ (1) a>0 $ 이며

$ (2) f(z) $가 $\lim_{R \to \infty} |f(Re^{i\theta})|=0$을 만족하는(well-behaved) 함수일 때,

'무한한 크기를 가지며 양의 허수축에 정의되는 반원'을 따라서 다음의 적분을 계산한 결과는 $0$이라는 것이다.

$$ \int_{-\infty}^{\infty} dz\ f(z)e^{iaz}$$

$$ \\ $$ 앞서 설명한 경우에서는, 아래의 적분에서

$$ \mathcal{A} = \frac{-i}{(2\pi)^2|\boldsymbol{x}|}\left(\int^\infty _{-\infty } d|\boldsymbol{p} |\ |\boldsymbol{p}| e^{i|\boldsymbol{p}||\boldsymbol{x}|} \ e^{-it\sqrt{|\boldsymbol{p}|^2 + m^2}} \right) \\ $$

$a$가 $|x|$이고 $f(z)$는 $|\boldsymbol{p}| e^{-it\sqrt{|\boldsymbol{p}|^2 + m^2}}$에 대응된다.

$|x|$는 공간(space)에 대해 정의되는 값으로서 $0$보다 크고, 함수 $|\boldsymbol{p}| e^{-it\sqrt{|\boldsymbol{p}|^2 + m^2}}$의 값을 $|p|=z=Re^{i\theta}$로 두고 $R$의 값을 증가시켜서 보면

$z$의 허수부의 값도 증가할 것이다.

따라서, 아래와 같이 ($\exp$함수의 지수는 실수부와 허수부를 모두 포함하므로) 허수부의 영향만을 살펴보면

$$ z\exp\left[{-it\sqrt{{\text{\{i(Im[z])}\}}^2 + m^2}}\right]=z\exp\left[{-it\sqrt{-\text{Im}[Re^{i\theta}]+ m^2}}\right]\\ =z\exp\left[{-it\sqrt{-R\sin \theta +m^2}}\right] \\ =z\exp\left[{-t\sqrt{R\sin \theta - m^2}}\right] \\ (\because i=\sqrt{-1}) $$

이므로 $R\to\infty$의 극한에서 해당 값은 $0$이다. ($R$의 증가에 따라, $z$의 증가에 비해 $\exp$함수의 감소가 더욱 빠르다.)

$$ \\ $$

1. Tom Lancaster and Stephen J. Blundell, Quantum Field Theory for the Gifted Amateur, 2014.