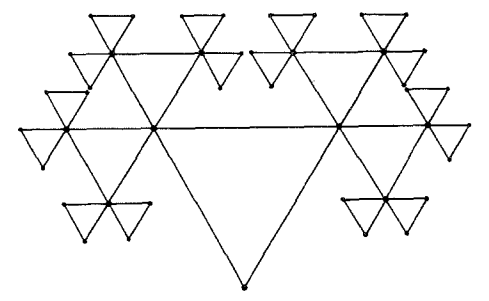
Kagome 격자는 다음 그림과 같은 구조를 갖는다. (참고문헌 1의 그림 1.)

실선에 해당하는 것이 kagome 격자 구조이며, 끊어져 있는 선은 벌집(honeycomb) 격자 구조에 해당한다.

이러한 Kagome 격자에서, 다음과 같은 해밀토니안을 갖는 이징 모형을 고려하자.

$$ \mathcal{H}=-J_3 \sum_{\Delta}\sigma_i \sigma_j \sigma_k -J_2\sum _{\text{n.n}}\sigma_i \sigma_j - h\sum_i \sigma_i $$

첫 번째 항은 $i,j,k$의 마디가 이루는 삼각형에 대한 상호작용이고, 두 번째 항은 가장 근접한 이웃(nearest neighbor) 쌍에 대한 상호작용이며, 마지막 항은 각 마디의 스핀과 자기장에 대한 항이다.

$$ \\ $$ Kagome 격자에 대해서 정확한 해와 다이어그램을 얻은 논문은 첫 번째 참고문헌에 해당한다.

다만, (일종의 근사법으로서) Husimi 트리(tree) 구조에서의 이징 모형에 대해서 풀이한 뒤, 그 결과를 이용해서 kagome 격자 구조에서의 결과를 이해하는 방법도 있다.

Husimi 트리는 다음과 같은 구조이다. (참고문헌 2의 그림 2.(B), $\gamma-1$개의 삼각형을 각 노드에 붙이는 방식으로 구성되며, 그림에서는 $\gamma=3$이다.)

$$ \\ $$ 우선, Husimi tree 구조에서의 '국소적 자화량(local magnetization)'을 다음과 같이 쓰자.

$$ \langle \sigma_0 \rangle = \sum_\sigma \sigma_0 P(\sigma) /Z$$ 이때, 분배함수 $Z=\sum_\sigma P(\sigma)$ 이다. $P(\sigma)$는 아래와 같이 표현된다.

$$ P(\sigma ) = \exp\left[\beta\bigg\{J_3 \sum_{\Delta}\sigma_i \sigma_j \sigma_k + J_2 \sum_{\text{n.n}}\sigma_i\sigma_j + h\sum_i \sigma_i \bigg\}\right]$$

이때, Husimi tree의 구조에 대하여 다음의 식을 정의해보자.

$$ g_n(\sigma_0) = \sum_{\{\sigma_1\}} \exp\Bigg[\beta\Bigg(J_3\sum_\Delta \sigma_0\sigma_1^{(1)} \sigma_2^{(2)} + J_2 \sum_{\text{n.n}}\sigma_0 \sigma_1 + h \sum _{j=1,2}\sigma_1^{(j)} \Bigg) \Bigg][g_{n-1}(\sigma_1^{(1)})]^{\gamma-1}[g_{n-1}(\sigma_1^{(2)})]^{\gamma-1} $$

여기서 $\sigma_1^{(j)}$은 sub-tree 중 ($\sigma_0$을 제외한) $j$ 번째에 연결되어 있는 스핀을 가리키는 표현이다.

$$ \\ $$ 이러한 방식의 정의는 Husimi 트리가 트리 구조를 가지기에 가능한 것이다. 그에 따라, 분배함수 $Z=\sum_\sigma P(\sigma)$를 다음과 같이 적을 수 있다.

$$ Z = \sum_{\sigma_0} \exp(\beta h\sigma_0) [g_n(\sigma_0)]^{(\gamma-1)} $$

따라서,

$$ \langle \sigma_0 \rangle = Z^{-1} \sum_{\sigma_0} \sigma_0 \exp (\beta h\sigma_0 )[g_n(\sigma_0)]^{(\gamma-1)} $$ 로 쓸 수 있다.

$$ \\ $$

이때, $z_n$이라는 값을 아래와 같이 정의하자.

$$ z_n = g_n(+)/g_n(-) $$

그렇다면 $\langle \sigma_0 \rangle$는 다음과 같이 쓰여진다.

$$ \begin{align} \langle \sigma_0 \rangle &= \frac{\sum_{\sigma_0}\sigma_0 \exp(\beta h\sigma_0) [g_n(\sigma_0)]^{(\gamma-1)}}{Z} \\ &= \frac{e^{\beta h}g_n(+)^{(\gamma-1)}\ - \ e^{-\beta h}g_n(-)^{(\gamma-1)}}{e^{\beta h}g_n(+)^{(\gamma-1)}\ + \ e^{-\beta h}g_n(-)^{(\gamma-1)}} \\ &= \frac{e^{2\beta h}g_n(+)^{(\gamma-1)} \ -g_n(-)^{(\gamma-1)}}{e^{2\beta h}g_n(+)^{(\gamma-1)} \ +g_n(-)^{(\gamma-1)}} \\ &= \frac{az_n^{(\gamma-1)} \ -1}{az_n^{(\gamma-1)} \ +1} \end{align} $$ 여기에서 $a=e^{2\beta h}$ 이다.

$$\\ $$

$z_n$에 대해서는 $g_n(\sigma_0)$의 식을 사용해서 map을 얻을 수 있다.

우선, 앞서 살펴본

$$ g_n(\sigma_0) = \sum_{\{\sigma_1\}} \exp\Bigg[\beta\Bigg(J_3\sum_\Delta \sigma_0\sigma_1^{(1)} \sigma_2^{(2)} + J_2 \sum_{\text{n.n}}\sigma_0 \sigma_1 + h \sum _{j=1,2}\sigma_1^{(j)} \Bigg) \Bigg][g_{n-1}(\sigma_1^{(1)})]^{\gamma-1}[g_{n-1}(\sigma_1^{(2)})]^{\gamma-1} $$

의 식에서, $g_n(+)$와 $g_n(-)$를 다음과 같이 구하는 것이다.

$$ \begin{align} g_n(+) &= e^{\beta(J_3+3J_2+2h)}g_{n-1}^{(\gamma-1)}(+)g_{n-1}^{\gamma -1}(+) \\ &\ \ + 2e^{\beta(-J_3+J_2)}g_{n-1}^{(\gamma-1)}(+)g_{n-1}^{\gamma -1}(-) \\ &\ \ +e^{\beta(J_3 - J_2 -2h)}g_{n-1}^{(\gamma-1)}(-)g_{n-1}^{\gamma -1}(-), \\ \\ g_n(-) &= e^{\beta(-J_3 -J_2 +2h)}g_{n-1}^{(\gamma-1)}(+)g_{n-1}^{\gamma -1}(+) \\ &\ \ + 2e^{J_3-J_2}g_{n-1}^{(\gamma-1)}(+)g_{n-1}^{\gamma -1}(-) \\ &\ \ + e^{\beta(-J_3 +3J_2 -2h)}g_{n-1}^{(\gamma-1)}(-)g_{n-1}^{\gamma -1}(-). \end{align} $$ 그리고, $z_n=g_n(+)/g_n(-)$를 다음과 같이 구할 수 있다.

$$ z_n = \frac{e^{\beta(J_3+3J_2+2h)}z_{n-1}^{2(\gamma-1)} + 2e^{\beta(-J_3 + J_2)}z_{n-1}^{\gamma-1} +e^{\beta(J_3 - J_2 -2h)}} {e^{\beta(-J_3 -J_2 +2h)}z_{n-1}^{2(\gamma-1)} + 2e^{\beta(J_3-J_2)}z_{n-1}^{\gamma-1} + e^{\beta(-J_3 +3J_2 -2h)}} $$

위의 식은 분모와 분자에 $g_{n-1}^{(\gamma-1)}(-)g_{n-1}^{\gamma -1}(-)$를 나누어준 결과이다.

또한, 다음과 같은 변수들을 새로 정의하고

$$ a= e^{2\beta h},\ b=e^{2\beta J_2 },\ c=e^{2\beta J_3} $$

$z_n$을 다음과 같이 정리하자.

$$ z_n = \frac{c^{1/2}b^{3/2}a z_{n-1}^{2(\gamma-1)} + 2c^{-1/2}b^{-1/2}z_{n-1}^{\gamma -1}+ c^{1/2}b^{-1/2}a^{-1}}{c^{-1/2}b^{-1/2}az_{n-1}^{2(\gamma-1)} +2c^{1/2}b^{-1/2}z_{n-1}^{\gamma-1}+c^{-1/2}b^{3/2}a^{-1}} $$

$$ \\ $$

$$ = \frac{a^2b^2c z_{n-1}^{2(\gamma-1)} + 2az_{n-1}^{\gamma -1}+ c}{a^2z_{n-1}^{2(\gamma-1)} +2acz_{n-1}^{\gamma-1}+b^2}. $$

위의 식의 마지막 등식은 분모와 분자에 $c^{-1/2}b^{-1/2}a^{-1}$을 나누어줌으로써 얻었다.

$$ \\ $$

따라서 우리는 $x_n$에 대하여 다음의 map을 얻은 것이다.

$$z_n=f(z_{n-1}), \quad f(z) = \frac{a^2b^2cz^{2(\gamma-1)}+2az^{\gamma-1}+c}{a^2z^{2(\gamma-1)} + 2acz^{\gamma-1} +b^2}$$

1. Exact results for lattice models with pair and triplet interactions, X N Wu and F Y Wu, 1989.

2. Phase diagrams of Ising models on Husimi trees II. Pair and multisite interaction systems, 1992.

3. Thermodynamic approach to three-site antiferromagnetic Ising model in chaotic region, N.S. Ananikian and S.K. Dallakian, 2018.