2차원 XY모형의 해밀토니안은 다음과 같다. $$\beta H = -K\sum_{\langle mn\rangle} \cos(\theta_m-\theta_n)$$

위 해밀토니안에서 몇가지 변환을 거치면 다음과 같은 Sine-Gordon모형의 꼴과 같아진다. $$Z(K,y) = \int [\mathcal D\phi(\mathbf r)] \exp\left[\int d^dr \left\{-\frac12 \vert\nabla\phi\vert^2+2y\cos(2\pi\sqrt K\phi(\mathbf r))\right\}\right]$$ 여기서 $y$는 소용돌이의 퓨가시티(vortex fugacity)이다. 지금부터 이를 운동량 껍질 재규격화(Momentum shell RG)방법을 사용해 분석해보고자 한다. 재규격화는 간단히 말해 coarse-graining과 rescaling 이 두 과정으로 이루어지는데 이를 간단히 그림으로 나타내면 다음과 같다. 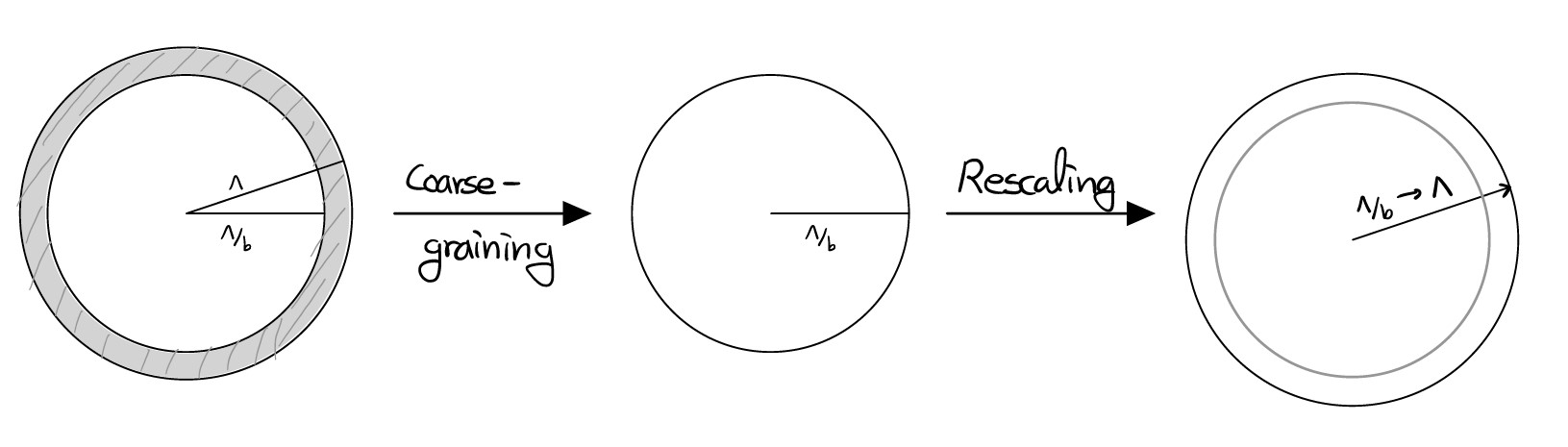아래 계산에서는 축척인자를 $b=e^s$로 둘 것이다. 이를 위해 먼저 장 $\phi(\mathbf r)$를 다음 두 항으로 쪼개어 나타내자. $$\phi(\mathbf r) = \frac{1}{(2\pi)^2}\int d^2k e^{i\mathbf k\cdot\mathbf r}\phi(\mathbf k) = \underbrace{\frac{1}{(2\pi)^2}\int_0^{\Lambda/b} d^2k e^{i\mathbf k\cdot\mathbf r}\phi(\mathbf k)}_{\phi_l(\mathbf r)} + \underbrace{\frac{1}{(2\pi)^2}\int_{\Lambda/b}^\Lambda d^2k e^{i\mathbf k\cdot\mathbf r}\phi(\mathbf k)}_{\phi_s(\mathbf r)}$$ 이렇게 하면 원래의 유효 해밀토니안도 쪼개어 나타낼 수 있다. $$\Rightarrow \mathcal H[\phi_l,\phi_s] = \mathcal H_{0,l}[\phi_l] + \mathcal H_{0,s}[\phi_s] + V[\phi_l,\phi_s]$$ 여기서 각 항은 $$\mathcal H_{0,l}[\phi_l] = \frac12 \int d^2r \vert\nabla\phi_l\vert^2,\quad \mathcal H_{0,s}[\phi_s] = \frac12 \int d^2r \vert\nabla\phi_s\vert^2$$ $$V[\phi_l,\phi_s] = -2y\int d^2r \cos\left(2\pi\sqrt K(\phi_l(\mathbf r)+\phi_s(\mathbf r))\right)$$ 이다. 우리는 일단 $y$가 작은 영역에 관심이 있으므로 $V[\phi_l,\phi_s]$를 섭동항으로 취급할 것이다. 첫 단계인 coarse-graining에서는 운동량 공간의 껍질에 해당하는 $\phi_s$를 모두 적분해서 \begin{eqnarray*} e^{-\mathcal H'[\phi_l]} &=& \int\mathcal D\phi_s(\mathbf r)e^{-\mathcal H_{0,l}[\phi_l] - \mathcal H_{0,s}[\phi_s] - V[\phi_l,\phi_s]}\\ &=& e^{-\mathcal H_{0,l}[\phi_l]}\frac{\int\mathcal D\phi_s(\mathbf r)e^{-V[\phi_s,\phi_l]-\mathcal H_{0,s}[\phi_s]}}{\int \mathcal D\phi_se^{-\mathcal H_{0,s}[\phi_s]}} \cdot\int \mathcal D\phi_se^{-\mathcal H_{0,s}[\phi_s]} \end{eqnarray*} \begin{eqnarray*} \Rightarrow\mathcal H'[\phi_l] &=& \mathcal H_{0.l}[\phi_l] -\log \left\langle e^{-V[\phi_s,\phi_l]}\right\rangle+\log \left[\int \mathcal D\phi_se^{-\mathcal H_{0,s}[\phi_s]}\right]\\ &=&\mathcal H_{0.l}[\phi_l] + \langle V\rangle_s -\frac12 \left(\langle V^2\rangle_s - \langle V\rangle_s^2\right)+\mathcal O(y^3) \end{eqnarray*} 이와 같이 재규격화된 유효 해밀토니안을 얻을 것이다. 윗 줄의 마지막 $\log$항은 상호작용 상수의 변화에 아무런 영향도 미치지 못하므로 지금부터 무시하고, 아랫 줄로 내려올 때는 큐물런트 전개를 사용하였다.

먼저 1차항에 해당하는 $\langle V\rangle_s$를 계산해보고자 한다. $\cos$ 항의 기댓값을 계산하는 것 보다 지수함수의 기댓값은 큐물런트 전개를 사용해서 비교적 쉽게 계산할 수 있기 때문에 삼각함수를 다음과 같은 지수함수의 형태로 변환하고 \begin{eqnarray*} \langle V\rangle_s &=& -2y\int d^2r \langle\cos\left(\alpha\phi_l(\mathbf r) + \alpha\phi_s(\mathbf r)\right)\rangle_s\qquad\text{where}\enspace \alpha = 2\pi\sqrt K\\ &=&-2y\int d^2r \,\text{Re}\langle e^{i\alpha(\phi_l(\mathbf r) + \phi_s(\mathbf r))}\rangle_s\\ &=&-2y\int d^2r \,\text{Re}\left[\left\langle e^{i\alpha\phi_s(\mathbf r)}\right\rangle_se^{i\alpha\phi_l(\mathbf r)}\right]\\ \end{eqnarray*} $\langle\cdot\rangle_s$항을 계산하면 \begin{eqnarray*} \log\langle e^{i\alpha\phi_s(\mathbf r)}\rangle_s &=& i\alpha\langle\phi_s(\mathbf r)\rangle_s - \frac12 (i\alpha)^2 \left(\left\langle \phi_s^2(\mathbf r)\right\rangle_s - \langle \phi_s(\mathbf r)\rangle_s^2\right)\\ &=& \frac12 \alpha^2 \langle \phi_s^2(\mathbf r)\rangle_s\\ &=& \frac12 \alpha^2 \langle \phi_s(\mathbf 0)\phi_s(\mathbf 0)\rangle_s\\ &=& \frac12 \alpha^2\int_{\Lambda/b}^\Lambda\int_{\Lambda/b}^\Lambda\frac{d^2k_1}{(2\pi)^2}\frac{d^2k_2}{(2\pi)^2}\left\langle\phi(\mathbf k_1)\phi(\mathbf k_2)\right\rangle_s\\ &=& \frac12 \alpha^2\int_{\Lambda/b}^\Lambda\frac{d^2k}{(2\pi)^2}\frac{1}{k^2}\\ &=& \frac{\alpha^2}{4\pi}\int_{\Lambda/b}^\Lambda \frac{dk}{k}\\ &=& \frac{\alpha^2}{4\pi}\log b = -\frac{\alpha^2}{4\pi}s\\ \Rightarrow \langle e^{i\alpha\phi_s(\mathbf r)}\rangle_s &=&e^{-\alpha^2s/4\pi} \approx1-\frac{\alpha^2s}{4\pi} \end{eqnarray*} 를 얻는다. 따라서 $\langle V\rangle_s$는 \begin{eqnarray*} \langle V\rangle_s &=&-2y\int d^2r\,\text{Re}\left[\left\langle e^{i\alpha\phi_s(\mathbf r)}\right\rangle_se^{i\alpha\phi_l(\mathbf r)}\right]\\ &=&-2y\left(1-\frac{\alpha^2s}{4\pi}\right)\int d^2r \cos(\alpha\phi_l(\mathbf r)) \end{eqnarray*} 이다. 이를 가지고 재규격화된 해밀토니안을 \begin{eqnarray*} \Rightarrow\mathcal H'[\phi_l] &=&\mathcal H_{0.l}[\phi_l] + \langle V\rangle_s\\ &=&\int d^2r\left\{\frac12\vert\nabla\phi_l\vert^2 - 2y\left(1-\frac{\alpha^2s}{4\pi}\right)\cos(\alpha\phi_l(\mathbf r))\right\} \end{eqnarray*} 와 같이 쓸 수 있다. 이 다음으로는 축척인자 $b$만큼 줄어든 운동량 공간을 원래대로 돌려놓아야 한다. 이 작업이 위 그림 두번째 화살표에 해당하는 rescaling 과정이다.