This is an old revision of the document!
두 가지 관점
빈도론(frequentism) 혹은 객관주의(objectivism)
- 모집단의 특성을 나타내는 매개변수는 고정된 상수로서 우리에게 알려져 있지 않다.
- 확률은 장기간에 걸친 상대적 빈도로 해석된다.
- 통계적 절차는 실험을 무한히 반복했을 때의 결과를 통해 평가된다.
베이즈 학파(bayesian) 혹은 주관주의(subjectivism)
- 매개변수의 실제 값이 우리에게 불확실하므로 이를 확률변수로 취급한다.
- 확률 법칙은 매개변수에 대한 추론을 위해 직접 사용된다.
- 매개변수에 대한 확률적 진술은 “믿음의 정도”로 해석되어야 한다. 사전(prior) 확률은 주관적이어서 각자는 자신의 사전 확률을 다르게 가질 수 있으며 이는 개인이 매개변수의 가능한 값들에 얼마만큼의 가중치를 주는지에 해당한다. 즉 데이터를 관찰하기 전에 매개변수의 값이 이 정도라는 게 얼마나 그럴 듯한지 생각하는 정도이다.
- 데이터를 수집하면서 베이즈의 정리를 따라 매개변수에 대한 우리의 믿음을 고쳐나간다. 이를 통해 사후(posterior) 확률을 얻는다.
베이즈의 정리
조건부 확률의 정의로부터 $$ P(B|A) = \frac{P(A \cap B)}{P(A)}= \frac{P(A \cap B)}{P(A \cap B) + P(A \cap \overline{B})} = \frac{P(A|B)P(B)}{P(A|B)P(B) + P(A|\overline{B})P(\overline{B})}. $$ 이 식은 $P(A|B)$와 $P(B|A)$를 연결지어준다.
분모에 등장하는 것처럼 가능한 $B$의 사건에 대해 더함으로써 얻어지는 확률은 주변(marginal) 확률이라고도 불린다: $$P(A) = P(A \cap B) + P(A \cap \overline{B}).$$
베이즈의 정리를 이용한 추론
첫 번째 예
5개의 공이 담긴 항아리가 있다. 공의 일부는 빨간색, 나머지는 녹색이지만 몇 개가 빨간색인지는 모른다. 확률변수 $X$가 항아리 속 빨간색 공의 갯수라고 하자. $X$의 가능한 값은 $x_i = 0, \ldots, 5$이다. 아무 정보가 없으므로 모든 값들이 동등하게 가능하다고 생각하자. 그러면 사전 확률은 $g(0) = g(1) = \ldots = g(5) = 1/6$이다.
무작위로 공을 하나 골라내자. 확률 변수 $Y$는 빨간 공이 나오면 1이고 아니면 0이다. 그러면 조건부 확률은 $P(Y=1|X=x_i) = i/5$이고 $P(Y=0|X=x_i) = (5-i)/5$이다. 이를 '가능도(likelihood)'라고 부른다. 결합 확률(빨간 공이 $x_i$ 개 있고 내가 빨간 공을 뽑을 확률)은 가능도에 사전 확률을 곱하면 되므로(주변확률이 $1/2$임에 유의한다), 만일 빨간 공이 나왔다고 하면 아래 표처럼 사후 확률을 얻는다. 즉 이것이 빨간 공을 관찰한 후 내가 가지고 있는 $X$에 대한 믿음을 나타낸다.
| $x_i$ | 사전 확률 | 가능도 | 사전$\times$가능도 | 사후 확률 |
|---|---|---|---|---|
| 0 | 1/6 | 0/5 | 0/30 | 0/15 |
| 1 | 1/6 | 1/5 | 1/30 | 1/15 |
| 2 | 1/6 | 2/5 | 2/30 | 2/15 |
| 3 | 1/6 | 3/5 | 3/30 | 3/15 |
| 4 | 1/6 | 4/5 | 4/30 | 4/15 |
| 5 | 1/6 | 5/5 | 5/30 | 5/15 |
| 합 | 1/2 | 1 |
공을 하나 더 뽑아보자 (빼낸 공을 다시 집어넣지 않는다). 이번에는 녹색 공이 나왔다고 해보자. 앞에서의 사후 확률이 이번에는 사전 확률이 되고 여기에서 갱신되는 확률 분포가 아래 표에 있다.
| $x_i$ | 사전 확률 | 가능도 | 사전$\times$가능도 | 사후 확률 |
|---|---|---|---|---|
| 0 | 0 | ?? | 0 | 0 |
| 1 | 1/15 | 4/4 | 1/15 | 1/5 |
| 2 | 2/15 | 3/4 | 1/10 | 3/10 |
| 3 | 3/15 | 2/4 | 1/10 | 3/10 |
| 4 | 4/15 | 1/4 | 1/15 | 1/5 |
| 5 | 5/15 | 0/4 | 0 | 0 |
| 합 | 1/3 | 1 |
이렇게 한 번씩 사후 확률을 갱신하는 방법도 있고 두 번의 관찰을 동시에 고려해서 사후 확률을 만드는 방법도 있을 것이다. 이 둘은 정확히 같은 결과를 준다.
두 번째 예
큰 모집단에서 $p$라는 비율이 어떤 특징을 가지고 있고 나머지는 가지고 있지 않다고 하자. $n$ 번을 독립적으로 시도해서 그 특징을 가진 사람 $y$ 명을 뽑을 확률은 이항 분포로 주어질 것이다: $$f(y|p) = \binom{n}{y} p^y (1-p)^{n-y}.$$ $y$를 고정한 상태에서 $p$가 변화한다고 생각하면 위의 식이 가능도가 된다.
베이즈의 정리를 사용하려면 $p$의 값에 대한 우리의 믿음을 반영하는 사전 확률 $g(p)$가 있어야 한다. 사후 확률은 사전 확률이 가능도를 곱해서 얻어진다: $g(p|y) \propto g(p) \times f(y|p)$. 위의 예에서도 보듯이 분모에 주변확률이 있어야 등호로 쓸 수 있는데 이는 상대적인 비율만을 바꾸어줄 뿐 크게 중요하지 않다.
사전 확률로 베타 함수를 사용한다고 해보자: $$g(\pi; a,b) = \frac{\Gamma(a+b)}{\Gamma(a) \Gamma(b)} p^{a-1} (1-p)^{b-1}.$$ 이 경우 사후 확률, 즉 해당 특성을 지닌 $y$명을 관찰한 상황에서 $p$의 확률 밀도 분포는 다시 베타 함수 꼴로 주어진다: $$g(\pi |y) = \frac{\Gamma(n+a+b)}{\Gamma(y+a) \Gamma(n-y+b)} p^{a+y-1} (1-p)^{b+n-y-1}.$$
참고로 베타 함수 $B(a,b)$의 평균은 $\mu = \frac{a}{a+b}$이고 표준편차는 $\sigma = \sqrt{\frac{ab}{(a+b)^2 (a+b+1)}}$이다. 이항분포의 경우와 비교해보면, 크기가 $n_{eq} = a+b+1$인 무작위 표본에 대응된다고 해석할 수 있다.
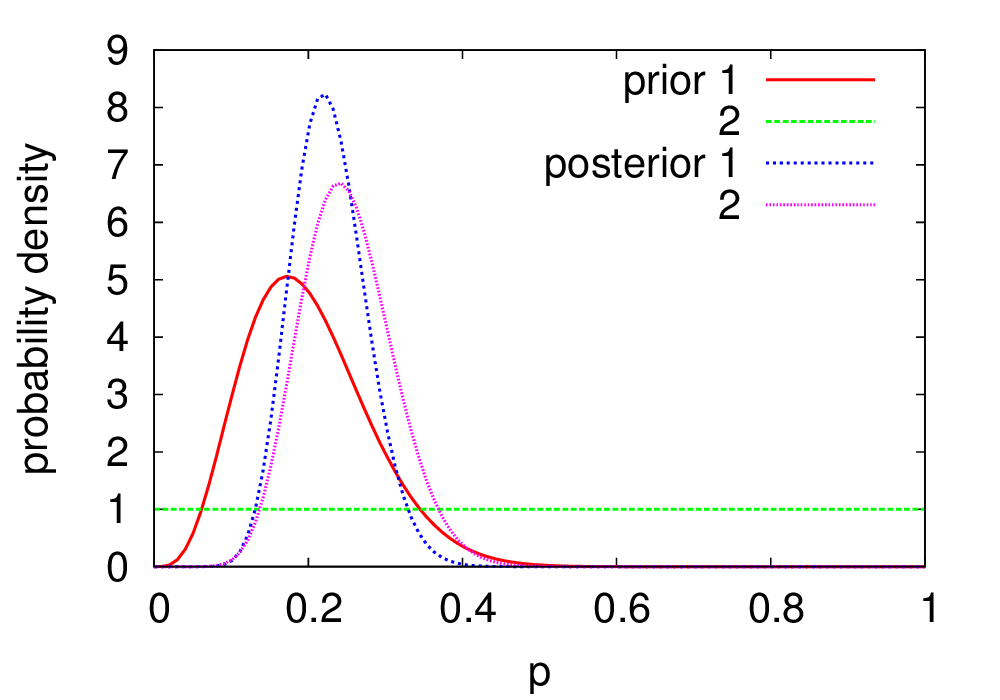
마을에 도박장이 들어서는 데 찬성하는 주민들의 비율 $p$에 대해, 영희와 철수가 각기 믿는 바가 있다고 하자. 영희의 믿음은 평균이 0.2이고 표준편차는 0.08이리라는 것이다. 이 $\mu$와 $\sigma$에 대한 식을 풀어 $a$와 $b$를 구하면 그녀의 믿음을 기술하는 베타 함수 $B(a,b)$를 정할 수 있는데, $a = 4.8$, $b=19.2$이다.
다른 한편, 철수는 최근에 이사를 와서 마을 사정을 잘 모르고, 따라서 어떤 $p$도 선호하지 않는 균일한 사전 확률 분포를 택했다. 이는 $a=b=1$에 해당한다.
그들은 50명의 주민을 골라서 도박장에 대한 의견을 물었다. 그랬더니 $y=12$ 명이 찬성의 뜻을 밝혔다. 그 결과 영희의 사후 확률은 $B(4.8+12, 19.2+38)$이 되었고 철수의 사후 확률은 $B(1+12, 1+38)$이 되었다. 아래 그림에서 보듯, 비록 철수와 영희의 처음 믿음은 사뭇 달랐지만 그들이 도달한 결론은 메우 비슷하다.
독립사건
$(\Omega, \mathcal{F}, \mathbp{P})$을 확률공간이라고 하자. $\mathcal{F}$의 사건 $A$와 사건 $B$가 $\mathbp{P}(AB)=\mathbp{P}(A)\mathbp{P}(B)$를 만족시킬 때 사건 $A$와 $B$는 독립이라 한다.
좀 더 일반적으로 사건의 모임 $\mathcal{A}_{1}$과 $\mathcal{A}_{2}$이 $\mathcal{A}_{1}$,$\mathcal{A}_{2}\in\mathcal{F}$이며 사건 $A_{1}$과 $A_{2}$에 대해 각각 $\mathcal{A}_{1} \in A_{1}$, $\mathcal{A}_{2} \in A_{2}$를 만족한다면 사건의 모임 $\mathcal{A}_{1}$과 $\mathcal{A}_{2}$은 독립이라 한다.
상호독립과 짝독립
$\mathpb{P}(A_{i_{1}} A_{i_{2}}\cdots A_{i_{k}})=\mathpb{P}(A_{i_{1}})\mathpb{P}(A_{i_{2}})\cdots\mathpb{P}(A_{i{k}})$가 $k=2,\ldots,n$, $1\leq i_{1}<i_{2}<\ldots<i_{k}\leq n$인 모든 $k$와 $i_{1},i_{2},\ldots,i_{k}$에 대해 만족된다면 $A_{1},\ldots,A_{n}\in \mathcal{F}$는 상호독립이라 한다. $k=n=2$인 경우에는 짝독립이라 한다.
상호독립과 짝독립의 관계
다음과 같은 상황을 생각하자.
겉보기에 차이가 없는 $16$개의 바구니가 앞에 놓여 있다. 바구니 안에는 $1$ 또는 $0$이 적힌 쪽지 하나씩이 들어 있는 공 $3$개가 각각 $1,2,3$이라고 표시되어 있다. 이 때, 우리가 바구니 하나를 열어서 $1$번 공에 $0$이 적힌 쪽지가 있을 지 $1$이 적혀 있을지 확인할 수 있을 것이다. 이러한 상황은 아래와 같이 표기될 수 있다.
$A_{i}=\{i번 째 공에 "1"이 표시된 경우\}, i=1,2,3$
함께 보기
참고문헌
- W. M. Bolstad, Introduction to Bayesian statistics (Wiley, Hoboken, NJ, 2007).