개요

$P(x)$와 $Q(x)$가 주어져있을 때, $y(x)$가 다음의 미분방정식을 만족한다고 하자: $$\frac{dy}{dx} + P(x)y(x) = Q(x)$$ 초기 조건이 $y(x=x_0)=y_0$로 주어진다면, 해는 형식적으로 다음처럼 쓸 수 있다: $$y(x) = e^{-I(x;x_0)} \int_{x_0}^x Q(x') e^{I(x';x_0)} dx' + y_0 e^{-I(x;x_0)}.$$ 이 때 $I(x;x_0) \equiv \int_{x_0}^x P(x') dx'$이다. 위 식 우변의 첫 번째 항이 $Q(x)$에 의해 추동되는 특수해(particular solution)이며 두 번째 항은 초기 조건을 맞춰주는 역할을 한다. 밑의 내용과 비교하기 위해 적분 앞의 지수함수를 적분 속의 지수함수와 합쳐서 써놓도록 하자: $$y(x) = \int_{x_0}^x e^{-I(x;x')} Q(x') dx' + e^{-I(x;x_0)} y_0.$$

위의 방정식은 분리가 되므로(separable) 이를 이용하여 간단하게 해를 구할 수 있다. 하지만 미분방정식에 연산자가 있는 경우에는 이 방법으로 해를 구할 수 없다. 즉, 예컨대 우변이 $0$인 동차 방정식에서

$$\frac{dy}{dx}+P(x)y(x)=0$$

에서 $P(x)$가 연산자라면

$$\frac{dy}{y} = -P(x)dx$$

이런 식으로 분리를 할 수 없다는 의미이다. 이런 경우, $y(x)$의 적분형을 구한 뒤 이것을 계속해서 적분 안에 대입하는 방법으로 해를 구할 수 있다.

$$\begin{align*} y(x) &= y_0 - \int_0^xdx_1P(x_1)y(x_1) \\ &= y_0 - \int_0^xdx_1P(x_1)\left[y_0-\int_0^{x_1}dx_2P(x_2)y(x_2)\right] \\ &= y_0 - \int_0^xdx_1P(x_1)y_0 + \int_0^xdx_1P(x_1)\int_0^{x_1}dx_2P(x_2)y_0 + \cdots + (-1)^n\int_0^xdx_1\int_0^{x_1}dx_2\cdots\int_0^{x_n}dx_{n-1}P(x_1)P(x_2)\cdots P(x_n)y_0 + \cdots \end{align*}$$

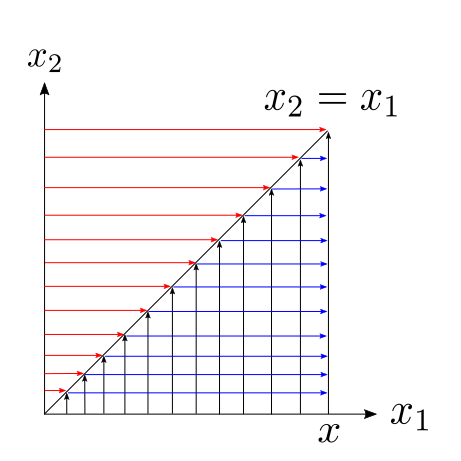
위의 그림을 참고하면 적분 구간은 아래처럼 바꿔 쓸 수 있다.

$$\int_0^xdx_1\int_0^{x_1}dx_2P(x_1)P(x_2) y_0 = \int_0^xdx_2\int_{x_2}^xdx_1P(x_1)P(x_2) y_0 = \int_0^xdx_1\int_{x_1}^xdx_2 P(x_2)P(x_1) y_0.$$

마지막 식은 중간 식에서 $x_1$과 $x_2$를 바꾸어 적은 것이며, 그림에서 검정색, 파란색, 빨간색으로 표시한 적분은 위의 적분식에서 순서대로 좌측, 중간, 우측 적분식을 의미한다.

작은 $x_i$ 쪽이 오른쪽에 오게끔 하는 시간정렬(time-ordering) 연산자 $\mathcal{T}$를 도입하자: $$\mathcal{T} P(x_1) P(x_2) = \left\{ \begin{array}{ll} P(x_1) P(x_2), & x_1 \ge x_2\\ P(x_2) P(x_1), & x_1 < x_2.\\ \end{array}\right.$$ 위에서 좌측과 우측의 적분식을 더하면 그림으로부터 $$\int_0^xdx_1\int_0^{x_1}dx_2P(x_1)P(x_2) y_0 + \int_0^xdx_1\int_{x_1}^xdx_2P(x_2)P(x_1) y_0 = \int_0^xdx_1\int_0^xdx_2 \mathcal{T}P(x_1)P(x_2) y_0 = \mathcal{T} \left[\int_0^xdx' P(x')\right]^2 y_0$$ 임을 알 수 있는데 좌변의 두 항이 같음을 보였으므로

$$\int_0^xdx_1\int_0^{x_1}dx_2P(x_1)P(x_2) y_0 = \mathcal{T}\frac{1}{2}\left[\int_0^xdx'P(x')\right]^2 y_0$$ 를 얻을 수 있다. 일반적으로는 $$\int_0^xdx_1\int_0^{x_1}dx_2\cdots\int_0^{x_{n-1}}dx_{n}P(x_1)P(x_2)\cdots P(x_{n}) y_0 = \mathcal{T}\frac{1}{n!}\left[\int_0^xdx'P(x')\right]^n y_0$$ 이어서, 결론적으로 해는 $$y(x) = \sum_{n=0}^\infty \mathcal{T}\frac{(-1)^n}{n!}\left[\int_0^xdx'P(x')\right]^n y_0 = \mathcal{T}\exp\left[-\int_0^xdx^\prime P(x^\prime)\right]y_0$$ 이다.

$n \ge 1$일 때($x_0 \equiv x$) $$(-1)^n \int_0^xdx_1\int_0^{x_1}dx_2\cdots\int_0^{x_{n-1}}dx_{n}P(x_1)P(x_2)\cdots P(x_{n}) y_0 = \mathcal{T}\frac{1}{n!}\left[- \int_0^xdx'P(x')\right]^n y_0$$ 에서 좌변을 $x$로 미분해보자.

$$\begin{eqnarray*} &&(-1)^n \frac{d}{dx} \int_0^xdx_1\int_0^{x_1}dx_2\cdots\int_0^{x_{n-1}}dx_{n}P(x_1)P(x_2)\cdots P(x_{n}) y_0 \\ &=& (-1)^n P(x) \int_0^{x}dx_2\cdots\int_0^{x_{n-1}}dx_{n}P(x_2)\cdots P(x_{n}) y_0 \\ &=& -P(x) \mathcal{T} \frac{1}{(n-1)!}\left[- \int_0^xdx'P(x')\right]^{n-1} y_0 \end{eqnarray*}$$

따라서 $$\frac{d}{dx} y(x) = -P(x) \sum_{n=0}^\infty \mathcal{T}\frac{1}{n!}\left[-\int_0^xdx'P(x')\right]^n y_0 = -P(x) y(x)$$ 이다.

우변의 $Q(x)$가 0이 아닌 경우에도 비슷하게 풀 수 있다. $$\frac{dy}{dx} = -P(x)y(x) + Q(x)$$ 를 $$y(x) = y_0 + \int_0^x dx_1 \left[ -P(x_1)y(x_1) + Q(x_1) \right]$$ 으로 쓴 다음 위에서처럼 계속 대입할 수 있다. 위에서 이미 등장한 항들 외에 $Q(x)$ 때문에 새로 등장하는 항들은 아래와 같다: $$\int_0^x dx_1 Q(x_1) - \int_0^x dx_1 \int_0^{x_1} dx_2 P(x_1) Q(x_2) + \int_0^x dx_1 \int_0^{x_1} dx_2 \int_0^{x_2} dx_3 P(x_1) P(x_2) Q(x_3) + \ldots.$$ 첫 번째 항은 변수명만 바꾸어두자: $$\int_0^x dx_1 Q(x_1) = \int_0^x dx' Q(x').$$ 두 번째 항의 적분 순서를 바꾼 다음 변수명을 바꾸어두자. $$\begin{eqnarray*} \int_0^x dx_1 \int_0^{x_1} dx_2 P(x_1) Q(x_2) &=& \int_0^x dx_2 \int_{x_2}^x dx_1 P(x_1) Q(x_2)\\ &=& \int_0^x dx' \int_{x'}^x dx'' P(x'') Q(x'). \end{eqnarray*}$$ 세 번째 항도 적분 순서를 바꾸어 $x_3$의 적분이 제일 바깥쪽에 오도록 한다. 이 때 변수 2개 사이에서 적분 순서를 바꾸는 일을 두 번 연속해서 하면 된다: $$\begin{eqnarray*} \int_0^x dx_1 \int_0^{x_1} dx_2 \int_0^{x_2} dx_3 P(x_1) P(x_2) Q(x_3) &=& \int_0^x dx_1 \int_0^{x_1} dx_3 \int_{x_3}^{x_1} dx_2 P(x_1) P(x_2) Q(x_3)\\ &=& \int_0^x dx_3 \int_{x_3}^x dx_1 \int_{x_3}^{x_1} dx_2 P(x_1) P(x_2) Q(x_3)\\ &=& \int_0^x dx_3 \left[ \int_{x_3}^x dx_1 \int_{x_3}^{x_1} dx_2 P(x_1) P(x_2) Q(x_3) \right]. \end{eqnarray*}$$ 괄호 안의 내용을 살펴보면, 앞의 동차 방정식에서 했던 것과 매우 유사하게 시간정렬 연산자 $\mathcal{T}$를 통해 표현할 수 있다: $$\int_{x_3}^x dx_1 \int_{x_3}^{x_1} dx_2 P(x_1) P(x_2) Q(x_3) = \frac{\mathcal{T}}{2} \left[ \int_{x_3}^x dx'' P(x'') \right]^2 Q(x_3).$$ 따라서 $Q(x)$로 인해 새로 등장한 항들을 다시 써보면 $$\begin{eqnarray*} &&\int_0^x dx' Q(x') - \int_0^x dx' \int_{x'}^x dx'' P(x'') Q(x') + \int_0^x dx' \frac{\mathcal{T}}{2} \left[ \int_{x'}^x dx'' P(x'') \right]^2 Q(x')\\ &=&\int_0^x dx' \left\{1 - \int_{x'}^x dx'' P(x'') + \frac{\mathcal{T}}{2} \left[ \int_{x'}^x dx'' P(x'') \right]^2 + \ldots \right\} Q(x')\\ &=&\int_0^x dx' ~~\mathcal{T} \exp \left[ - \int_{x'}^x dx'' P(x'') \right] Q(x'). \end{eqnarray*}$$ 전체 해는 다음처럼 쓸 수 있다: $$y(x) = \int_0^x dx' ~~\mathcal{T} \exp \left[ - \int_{x'}^x dx'' P(x'') \right] Q(x') + \mathcal{T}\exp\left[-\int_0^xdx^\prime P(x^\prime)\right]y_0$$