This is an old revision of the document!
직교하지 않는 좌표계에서의 벡터
표현
좌표계의 축들이 직교하지 않는다고 해보자. 이 때 벡터를 성분으로 나타내려면 두 가지 방안이 있을 수 있다.
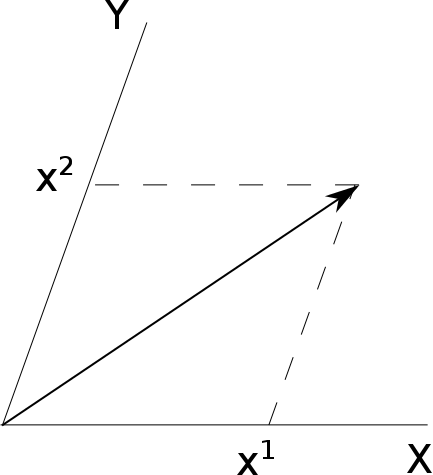
하나는 왼쪽처럼 축에 평행한 방향으로 선을 그어서 표현하는 방법이다. 이렇게 표현하는 벡터를 $\vec{r} = x^1 \vec{a}_1 + x^2 \vec{a}_2$라고 하자. $\vec{a}_i$는 적절한 기저 벡터이고, 윗 첨자는 제곱을 의미하는 것이 아님에 주의한다.
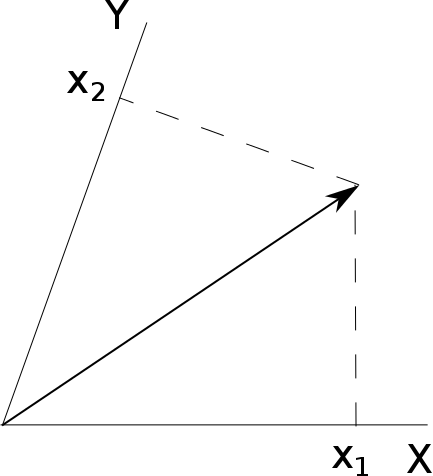
다른 방법은 오른쪽 그림처럼 축에 수선을 내림으로써 표현하는 것이다. 이렇게 표현하는 벡터를 $\vec{r} = x_1 \vec{a}^1 + x_2 \vec{a}^2$으로 적자. 마찬가지로 $\vec{a}^i$는 적절한 기저 벡터로, $\vec{a}_i$와 일반적으로 같지 않다.
좌표축이 수직하다면 이 두 표기법을 구분할 필요는 없다.
아인슈타인 표기법에 따르면 $\vec{r} = x_i \vec{a}^i = x^i \vec{a}_i$이며, 반면 $\vec{r} \neq x_i \vec{a}_i$이고 $\vec{r} \neq x^i \vec{a}^i$이다. 이제 이 둘을 같이 그려보자.
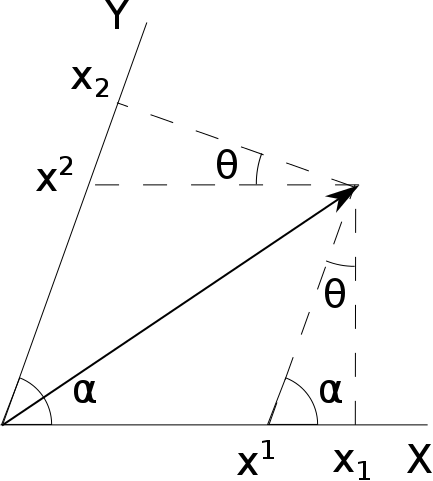
좌표축 사이의 각도를 $\alpha$라고 하자. 벡터의 화살표 끄트머리로부터 $x^1$으로 내려오는 선과 $x_1$으로 내려오는 선 사이의 각도를 $\theta$라고 하면, 위 그림 오른쪽의 삼각형으로부터 $\alpha+\theta = \pi/2$임을 쉽게 알 수 있다.
그 삼각형을 좀더 들여다보면, 밑변의 길이가 $x_1 - x^1$이고 가장 긴 변의 길이는 $x^2$이다. 둘 사이의 각도가 $\theta$이므로 다음의 식을 얻는다: $$ x_1 - x^1 = x^2 \sin \theta. $$ 마찬가지로 제일 위에 놓인 삼각형을 보면 $$ x_2 - x^2 = x^1 \sin \theta. $$ 임을 알게 된다. 다시 말해서, $$\begin{pmatrix} x_1 \\ x_2 \end{pmatrix} = \begin{pmatrix} 1 & \sin\theta\\ \sin\theta & 1 \end{pmatrix} \begin{pmatrix} x^1\\ x^2 \end{pmatrix} $$ 이라는 것이다. 중간의 $2 \times 2$ 행렬을 $g$라고 부르면 다음처럼 적을 수 있다: $$x_i = g_{ij} x^j.$$
거리잡기 텐서
위 그림에서 벡터의 길이 $r^2$은 코사인 법칙에 의해 $$r^2 = x^1 \times x^1 + x^2 \times x^2 - 2x^1 x^2 \cos(\pi - \alpha)$$ 이다. 위에서 $\alpha+\theta = \pi/2$임을 보였으므로 $\cos (\pi-\alpha) = -\cos\alpha = -\sin \theta$이고 따라서 $$r^2 = x^1 \times x^1 + x^2 \times x^2 + 2x^1 x^2 \sin\theta = \begin{pmatrix} x^1 & x^2 \end{pmatrix} \begin{pmatrix} 1 & \sin\theta\\ \sin\theta & 1 \end{pmatrix} \begin{pmatrix} x^1\\ x^2 \end{pmatrix} $$ 이다. 위에서 정의한 $g$가 다시 등장하였으므로 $$r^2 = x^i g_{ij} x^j = x^i x_i$$ 라고 줄여 쓸 수 있다.
좌표축 회전에 대한 변환식
반변
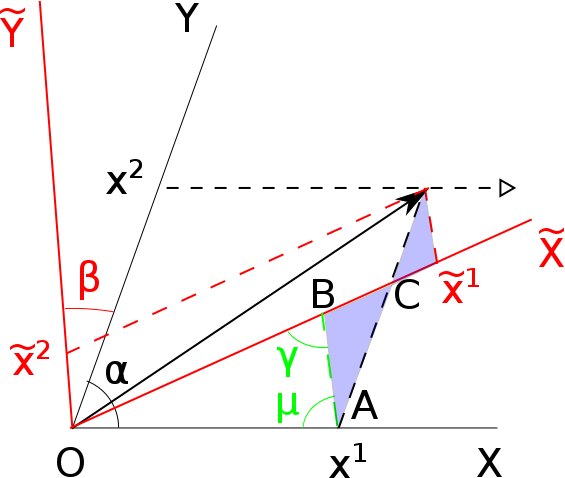
위의 좌표축을 각도 $\beta$만큼 회전시켜보자. 아래 그림처럼 벡터 $\vec{r}$은 이 새로운 좌표축 $(\tilde{X}, \tilde{Y})$에서 $\tilde{x}^1$과 $\tilde{x}^2$라는 성분으로 기술될 것이다.
설명의 편의를 위해, $O\tilde{Y}$에 평행하게 $A=x^1 \vec{a}_1$으로부터 $\tilde{X}$ 축 위로 선분을 긋자. 이 때에 만들어지는 각을 $\gamma$와 $\mu$라고 부르고 있다. 위 그림에서 이 두 각을 포함하고 있는 삼각형 OAB를 보면, 그 둘을 제외한 나머지 각 BOA는 단순히 회전각 $\beta$이므로 $\beta + \gamma + \mu = \pi$임을 알 수 있다.
삼각형 OAB에서 붉은 색으로 칠해진 변 OB의 길이는 사인 법칙에 의해 $x^1 \frac{\sin \mu}{\sin \gamma}$이다.
그 옆의 색칠된 삼각형 두 개는 서로 닮음인데, 그 중 큰 쪽을 보면, 아래에 놓인 예각 BAC는 $\beta$와 같고 왼쪽 위의 둔각 ABC는 $\pi - \gamma$와 같다. 따라서 사인 법칙을 다시 한번 이용하면, 이 삼각형에서 붉은 색 실선으로 나타낸 변 BC의 길이는 검은 점선으로 나타낸 변 AC의 $\frac{\sin \beta}{\sin \gamma}$ 배일 것이다
작은 삼각형도 닮음에 의해 마찬가지. 그리고 두 삼각형에서 검은 점선 두 개 길이의 합은 $x^2$에 다름 아니므로 결과적으로 우리는 $\tilde{x}^1$의 크기를 알게 되었다: $$\tilde{x}^1 = x^1 \frac{\sin\mu}{\sin\gamma} + x^2 \frac{\sin\beta}{\sin\gamma}.$$
다른 한편, $x_2$를 고정한 채 $x_1$을 늘려갈 때 $\tilde{x}_1$이 얼마나 변화하는지 생각해보자. 즉 위 그림에서 빈 화살표 방향으로 진행하는 것을 의미한다. 여기에서도 사인 법칙을 이용하면 그 변화량이 $$ \left( \frac{\partial \tilde{x}^1}{\partial x^1} \right)_{x^2} = \frac{\sin\mu}{\sin\gamma}$$ 임을 보일 수 있다.
또 이번에는 $x_1$를 고정한 채 $x_2$을 늘려갈 때 $\tilde{x}_1$이 얼마나 변화하는지를 생각해본다면, 이는 선분 AC를 연장시키며 진행하는 것에 대응하는데, 그 변화량은 다음과 같다: $$ \left( \frac{\partial \tilde{x}^1}{\partial x^2} \right)_{x^1} = \frac{\sin\beta}{\sin\gamma}.$$
다시 말해서, $$\tilde{x}^1 = \left( \frac{\partial \tilde{x}^1}{\partial x^1} \right)_{x^2} x^1 + \left( \frac{\partial \tilde{x}^1}{\partial x^2} \right)_{x^1} x^2$$ 이 성립하고 더 일반적인 표현식으로는 $$ \tilde{x}^j = \frac{\partial \tilde{x}^j}{\partial x^k} x^k $$ 이 된다.
공변
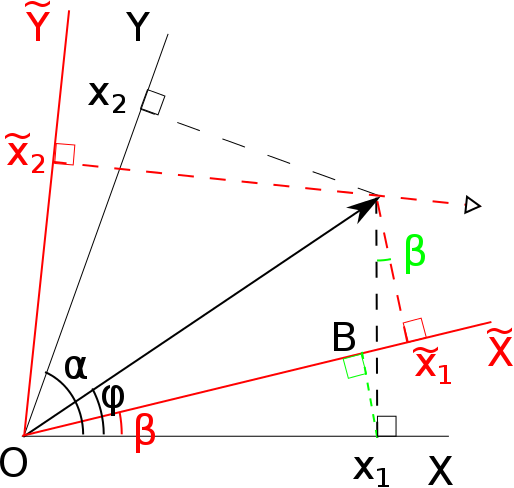
이번에는 축에 수선을 내린 경우에서 좌표축을 각도 $\beta$만큼 회전해보자.
$\tilde{x}_1$의 표현식을 구하려고 한다.
먼저 선분 OB의 길이는 $x_1 \cos\beta$임을 $X$ 축과 비교함으로써 알 수 있다.
나머지 부분의 길이를 구하기 위해, 벡터의 화살표 끝에서 $X$ 축으로 내린 검은색 점선을 보자. 여기에 $\sin\beta$를 곱하면 우리가 알고자 하는 길이가 된다.
그리고 벡터 $\vec{r}$의 길이를 $r$이라 하면 그 검은색 점선의 길이는 $r \sin\phi$이다.
요컨대, $\tilde{x}_1 = x_1 \cos\beta + r \sin\phi \sin\beta$이다.
그런데 벡터의 길이 $r$에 대해 다음 식이 성립함을 쉽게 알 수 있다. $$ r = \frac{x_1}{\cos\phi} = \frac{x_2}{\cos(\alpha-\phi)}. $$ 이를 통해 $r$을 소거하고 다음처럼 쓸 수 있다.
$$\tilde{x}_1 = x_1 \frac{\sin(\alpha-\beta)}{\sin\alpha} + x_2 \frac{\sin\beta}{\sin\alpha}.$$
그런데 $\tilde{x}_2$를 고정한 채 $\tilde{x}_1$을 증가시켰을 때 $x_1$이 얼마나 변화하는지를 보면 (빈 화살표 참조) $$ \left( \frac{\partial x_1}{\partial \tilde{x}_1} \right)_{\tilde{x}_2} = \frac{\sin(\alpha-\beta)}{\sin\alpha}$$ 임을 보일 수 있다.
마찬가지로 $\tilde{x}_2$를 고정한 채 $\tilde{x}_1$을 증가시켰을 때 $x_2$가 얼마나 변화하는지를 보면 $$ \left( \frac{\partial x_2}{\partial \tilde{x}_1} \right)_{\tilde{x}_2} = \frac{\sin\beta}{\sin\alpha}$$ 이다. 따라서 $$\tilde{x}_1 = \left( \frac{\partial x_1}{\partial \tilde{x}_1} \right)_{\tilde{x}_2} x_1 + \left( \frac{\partial x_2}{\partial \tilde{x}_1} \right)_{\tilde{x}_2} x_2$$ 이고 더 일반적으로 적으면 다음과 같다: $$\tilde{x}_j = \frac{\partial x_k}{\partial \tilde{x}_j} x_k.$$
두 벡터의 내적
위의 그림을 다시 한번 생각해보자. 사인 법칙에 의해 $$\frac{r}{\sin(\pi-\alpha)} = \frac{x^1}{\sin(\alpha-\phi)} = \frac{x^2}{\sin\phi}$$ 이므로 $$x^1 = r \frac{\sin(\alpha-\phi)}{\sin\alpha},$$ $$x^2 = r \frac{\sin\phi}{\sin\alpha}$$ 임을 알 수 있다.
다른 한편, 공변 성분은 간단히 $x_1 = r \cos\phi$, $x_2 = r \cos(\alpha-\phi)$이다.
위의 표현식들을 이용해 $\phi_1$ 방향을 가리키는 반변 벡터 $\vec{F}$와 $\phi_2$ 방향을 가리키는 공변 벡터 $\vec{s}$를 내적해보자: $$F^i s_i = F^1 s_1 + F^2 s_2 = F \frac{\sin(\alpha-\phi_1)}{\sin\alpha} s \cos\phi_2 + F \frac{\sin\phi_1}{\sin\alpha} s \cos(\alpha-\phi_2).$$ 이 때에 $F \equiv |\vec{F}|$, $s \equiv |\vec{s}|$이다. 코사인과 사인을 전개하고 정리하면 $$F^i s_i = F s \cos(\phi_1 - \phi_2)$$ 로서 올바른 결과를 얻는다.