개요

$P(x)$와 $Q(x)$가 주어져있을 때, $y(x)$가 다음의 미분방정식을 만족한다고 하자: $$\frac{dy}{dx} + P(x)y = Q(x)$$ 초기 조건이 $y(x_0)=y_0$로 주어진다면, 해는 형식적으로 다음처럼 쓸 수 있다: $$y(x) = e^{-I(x;x_0)} \int_{x_0}^x Q(x') e^{I(x';x_0)} dx' + y_0 e^{-I(x;x_0)}.$$ 이 때 $I(x;x_0) \equiv \int_{x_0}^x P(x') dx'$이다. 위 식 우변의 첫 번째 항이 $Q(x)$에 의해 추동되는 특수해(particular solution)이며 두 번째 항은 초기 조건을 맞춰주는 역할을 한다.

위의 방정식은 분리가 되므로(separable) 이를 이용하여 간단하게 해를 구할 수 있다. 하지만 미분방정식에 연산자가 있는 경우에는 이 방법으로 해를 구할 수 없다. 즉

$$\frac{dy}{dx}+P(x)y(x)=0$$

에서 $P(x)$가 연산자라면

$$\frac{dy}{y} = -P(x)dx$$

이런 식으로 분리를 할 수 없다는 의미이다. 이런 경우, $y(x)$의 적분형을 구한 뒤 이것을 계속해서 적분 안에 대입하는 방법으로 해를 구할 수 있다.

\begin{align*} y(x) &= y_0 - \int_0^xdx_1P(x_1)y(x_1) \\ &= y_0 - \int_0^xdx_1P(x_1)\left[y_0-\int_0^{x_1}dx_2P(x_2)y(x_2)\right] \\ &= y_0 - \int_0^xdx_1P(x_1)y_0 - \int_0^xdx_1P(x_1)\int_0^{x_1}dx_2P(x_2)y_0 + \cdots + (-1)^n\int_0^xdx_1\int_0^{x_1}dx_2\cdots\int_0^{x_n}dx_{n-1}P(x_1)P(x_2)\cdots P(x_n)y_0 + \cdots \end{align*}

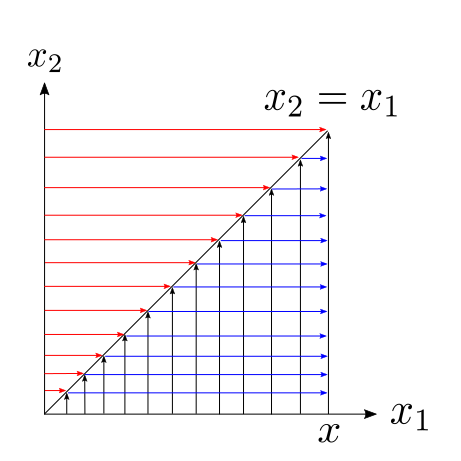
위의 그림을 참고하면 적분 구간은 아래처럼 바꿔 쓸 수 있다.

$$\int_0^xdx_1\int_0^{x_1}dx_2P(x_1)P(x_2) y_0 = \int_0^xdx_2\int_{x_2}^xdx_1P(x_1)P(x_2) y_0 = \int_0^xdx_1\int_{x_1}^xdx_2 P(x_2)P(x_1) y_0.$$

마지막 식은 중간 식에서 $x_1$과 $x_2$를 바꾸어 적은 것이며, 그림에서 검정색, 파란색, 빨간색으로 표시한 적분은 위의 적분식에서 순서대로 좌측, 중간, 우측 적분식을 의미한다.

작은 $x_i$ 쪽이 오른쪽에 오게끔 하는 정렬(ordering) 연산자 $\mathcal{T}$를 도입하자. 위에서 좌측과 우측의 적분식을 더하면 그림으로부터 $$\int_0^xdx_1\int_0^{x_1}dx_2P(x_1)P(x_2) y_0 + \int_0^xdx_1\int_{x_1}^xdx_2P(x_2)P(x_1) y_0 = \int_0^xdx_1\int_0^xdx_2 \mathcal{T}P(x_1)P(x_2) y_0 = \mathcal{T} \left[\int_0^xdx_1P(x_1)\right]^2 y_0$$ 임을 알 수 있는데 좌변의 두 항이 같음을 보였으므로

$$\int_0^xdx_1\int_0^{x_1}dx_2P(x_1)P(x_2) y_0 = \mathcal{T}\frac{1}{2}\left[\int_0^xdx_1P(x_1)\right]^2 y_0$$ 를 얻을 수 있다. 보다 일반적인 경우를 증명하기 위해 $x_1<x_2<\cdots<x_n<x$일 때

$$\int_0^xdx_1\int_0^{x_1}dx_2\cdots\int_0^{x_n}dx_{n-1}P(x_1)P(x_2)\cdots P(x_n) y_0 = \mathcal{T}\frac{1}{n!}\left[\int_0^xdx_1P(x_1)\right]^2 y_0$$

를 가정하자. 그리고 여기에 $x$에 대한 미분을 취하면

\begin{align*} \frac{d}{dx}\int_0^xdx_1\int_0^{x_1}dx_2\cdots\int_0^{x_{n+1}}dx_n P(x_1)P(x_2)\cdots P(x_n) y_0 &= P(x)\int_0^xdx_2\int_0^{x_2}dx_3\cdots\int_0^{x_n}dx_{n+1}P(x_1)P(x_2)\cdots P(x_n) y_0 \\ &= \mathcal{T} P(x) \frac{1}{n!}\left[\int_0^xdx_1P(x_2)\right]^n y_0 \\ &= \mathcal{T} \frac{d}{dx}\frac{1}{(n+1)!}\left[\int_0^xdx_1P(x_1)\right]^{n+1} y_0 \end{align*}

를 얻을 수 있고 위에서 $n=1$일 때 성립하는 것을 보였으므로 이것은 수학적 귀납법에 의해 자연수 $n$에 대해 일반적으로 성립한다는 것을 알 수 있다. 결론적으로 해는

$$y(x) = \sum_{n=0}^\infty \mathcal{T}\frac{(-1)^n}{n!}\left[\int_0^xdx_1P(x_1)\right]^n y_0 = \mathcal{T}\exp\left[-\int_0^xdx^\prime P(x^\prime)\right]y_0$$

이다.