입실론 기계(epsilon machine)은 시계열의 패턴을 찾기 위해 개발된 방법이다. 주어진 과거들에 대해 앞으로 나올 기호의 확률 분포를 보고 통계적으로 충분히 비슷할 경우 묶어서 하나의 '상태'로 간주한다는 것이 핵심 아이디어이다. '상태'들과 그 상태들 간의 전이확률은 시계열로부터 추출되며, 이런 전이의 모형들 중 정보 관점에서 가장 단순한 모형을 선택한다.

입실론 기계를 만들기 위한 한 가지 방법으로서, 시계열 뒤의 확률과정을 최대한 단순한 것으로 가정한 다음 단순한 가정이 설명하지 못하는 통계를 만나면 새로운 상태를 추가해 나간다.

이 예는 참고문헌 항목의 첫 번째인 Shalizi 등의 논문에서 가져온 것이며, 입실론 기계 구축의 세부적인 설명은 두 번째 참고문헌인 Cirera의 학위논문에서 가져온 것이다.

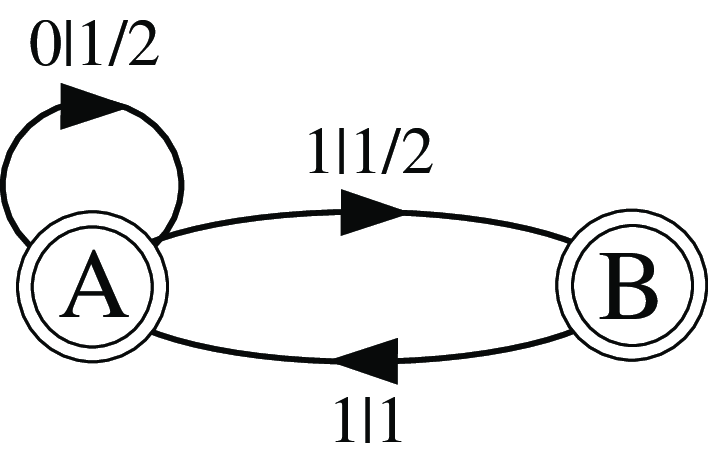
짝수 과정은 다음처럼 구성된다. 먼저 0,1로 이루어진 시계열 뒤에는 두 개의 숨은 상태 A, B가 존재한다. A는 1/2의 확률로 0을 내놓고 머무르거나 1을 내고 B로 전이한다. 반면 B는 언제나 1을 내고 A로 전이한다. 그 결과 1의 연쇄는 짝수번만 가능하고, 010, 01110, 0111110, … 처럼 홀수 번 나오는 것은 불가능하다. 그림으로 나타내면 아래와 같다 (Shalizi et al.):

짝수 과정이 특히 흥미로운 것은, 우리가 A와 B라는 숨은 상태를 찾지 않고 0과 1의 시계열 자체만을 본다면 절대로 마르코프 연쇄로 표현할 수 없는 과정이라는 점이다. 이는 1의 연쇄가 아무리 길게 이어져도 짝수와 홀수를 구분한다는 점에서 기억의 길이가 사실상 무한대이기 때문에 그러하다.

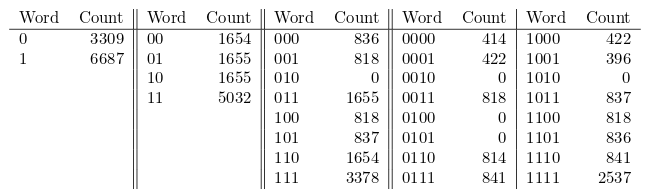
이 짝수 과정을 통해 길이가 1만인 시계열을 얻었고, 이로부터 다음과 같은 통계를 뽑아내었다고 하자(Shalizi et al.):

CSSR 알고리듬은 가장 간단한 가정에서부터 시작한다. 즉 아무런 기억 없이 일정한 확률로 0과 1이 나온다고 가정하는 것이다. 아무 기억이 없다는 뜻에서 $\emptyset$을 써놓고, 계의 상태가 이것 하나만 존재하므로 그 이름을 $A=\{ \emptyset \}$으로 놓자. 표의 가장 왼쪽을 보면, 상태 $A$에 있을 때 1이 따라나올 확률은 66.9%이다.

이제 직전에 나온 기호에 의존한다고 가정해보자. 표에서 왼쪽으로부터 두 번째 칸, 그러니까 00, 01 등의 빈도를 보여주는 영역을 보아야 한다.

• 0이 나왔을 때 다음에 1이 나올 확률은 1655/3309 = 50.0%이다. 이는 상태 $A$로부터 예측되는 것과는 다르다. 따라서 $B=\{0\}$이라는 상태를 새로 만들어야 한다.
• 1이 나왔을 때에 1이 따라나올 확률은 5032/6687=75.3%로서, 역시 $A$와는 다르고 $B$와도 다르다. 따라서 $C=\{1\}$을 새로운 상태로 추가한다.

$A=\{\emptyset\}$으로부터 파생된 위의 두 경우가 서로 다른 상태로 분리되므로 $A$는 그 자체로는 예측력이 없다. 따라서 $A$를 제거한다. 우리에게 남은 상태들은 $B=\{0\}$과 $C=\{1\}$ 두 개이다.

• C. R. Shalizi, K. L. Shalizi, and J. P. Crutchfield, An Algorithm for Pattern Discovery in Time Series (2002)
• M. P. Cirera, Applying Causal-State Splitting Reconstruction Algorithm to Natural Language Processing Tasks (Doctoral dissertation, Universitat Politècnica de Catalunya, 2008).