개요
Local mate competition. 한곳에 모인 적은 수의 개체들끼리만 짝짓기할 수 있을 때의 성비를 예측하는 이론.
수학적 모형
이배체
암컷에 작용하여 성비를 결정하는 대립유전자 $R$과 $S$가 존재한다고 가정하자. $R$은 원래 있던 유전자이고 $S$는 적은 수가 생겨난 돌연변이로 $R$에 대하여 우성이다. 그래서 한 어미가 $K$ 마리의 자손을 낳는다고 하면 $RR$인 어미는 $rK$ 마리의 아들과 $(1-r)K$ 마리의 딸을 낳는다. 반면 $SR$ 혹은 $SS$인 암컷은 $sK$ 마리의 아들과 $(1-s)K$ 마리의 딸을 낳는다.
이 생물의 생활사는 이렇다고 가정한다. $N$ 마리의 어미가 하나의 장소에 $K$ 개의 알을 낳는다. 알에서 깨어난 자손들은 이 장소 안에서 무작위로 짝짓기를 한다. 짝짓기 후 암컷들은 무작위로 흩어져 $N$ 마리씩 하나의 장소에 모여 알을 낳음으로써 주기를 순환한다. 짝짓기 시기가 지나면 수컷은 별다른 중요성을 가지지 않고, 우리는 한 장소에 모인 암컷들에만 주의를 기울일 것이다.
돌연변이가 아닌 보통의 개체에서 하나의 유전자가 딸을 거쳐서 복제되는 비율은 이러할 것이다: $W_0 = (1-r)K / 2$. 여기에서 $(1-r)K$는 이 개체가 낳은 딸의 수이고, 이배체로서 아비와 어미가 하나의 자손당 1/2의 기여도를 가져서 $1/2$를 곱한다.
$N-1$ 마리의 어미는 스스로도 짝도 돌연변이가 아닌데, 한 마리의 어미만 $SR$의 유전자형을 가진 채 $RR$ 수컷과 짝짓가 한 후 이 장소에 와있다고 해보자. $S$가 매우 드물다고 가정하면 이 경우만 고려해도 될 것이다 ($SR$ 수컷과 짝짓기한 $RR$ 어미의 경우도 있을 수 있지만 아래처럼 계산했을 때 $S$가 정확히 $W_0$만큼 복제되므로 이를 통해서는 $S$가 침범할 수 없다). 딸 세대에서 이 $S$ 유전자가 몇 개가 될 것인가?
먼저 이 장소에서 태어난 딸의 총 숫자는 $N_\text{daughters} = (N-1)(1-r)K + (1-s)K$이다. 이 중 $RR$인 어미로부터 태어난 딸은 물론 $(N-1)(1-r)K$이고 이들은 모두 $RR$인 암컷이다. $SR$인 어미로부터 태어난 딸 중 절반은 $SR$이고 나머지 절반은 $RR$이다. 따라서 $RR$인 딸의 숫자는 $(N-1)(1-r)K + (1-s)K/2$이고 $SR$인 딸의 숫자는 $(1-s)K/2$이다. 마찬가지로, $RR$인 아들의 숫자는 $(N-1)rK + sK/2$이고 $SR$인 아들의 숫자는 $sK/2$일 것이다.
그리고 이 아들들과 딸들끼리 짝짓기하여 $S$ 유전자가 전달되는 경우는 다음 세 가지이다:
- $SR$ 암컷 $\times$ $RR$ 수컷: 이렇게 만나는 사건의 확률은
$$P_{SR \times RR} = \left[\frac{(1-s)K/2}{(N-1)(1-r)K + (1-s)K}\right] \times \left[\frac{(N-1)rK+sK/2}{(N-1)rK + sK}\right]$$ 인데, 암컷의 $SR$ 중에서 $S$가 나와야 하므로 다시 확률 $1/2$을 곱한다.
- $RR$ 암컷 $\times$ $SR$ 수컷: 마찬가지로 이 사건의 확률은 아래와 같은데
$$P_{RR \times SR} = \left[\frac{(N-1)(1-r)K+(1-s)K/2}{(N-1)(1-r)K + (1-s)K}\right] \times \left[\frac{sK/2}{(N-1)rK + sK}\right]$$ 여기에 $1/2$을 곱한다.
- $SR$ 암컷 $\times$ $SR$ 수컷: 이렇게 만나는 사건의 확률은
$$P_{SR \times SR} = \left[\frac{(1-s)K/2}{(N-1)(1-r)K + (1-s)K}\right] \times \left[\frac{sK/2}{(N-1)rK + sK}\right]$$ 인데, 넘어가는 $S$의 수는 $1/4$의 확률로 2개, $1/2$의 확률로 1개이기 때문에 평균 1개가 된다. 즉 $1/2$를 곱할 필요가 없다.
따라서 $S$가 복제되는 수는 아래와 같다: \begin{eqnarray} W &=& N_\text{daughters} \left( \frac{1}{2} P_{RR \times SR} + \frac{1}{2} P_{RR \times SR} + P_{SR \times SR} \right)\\ &=& \frac{(1-s)K}{4} + \frac{sK}{4} \left[\frac{(1-s)+(1-r)(N-1)}{s+r(N-1)}\right]. \end{eqnarray}
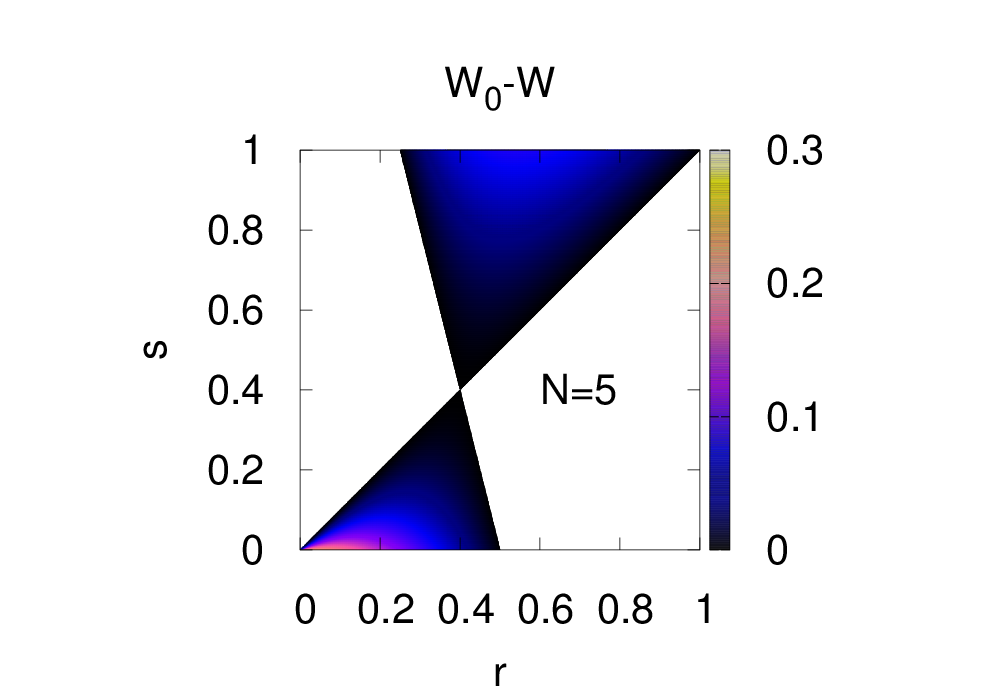
$W_0$가 $W$보다 크거나 같아야 돌연변이가 침입하지 못할 것이다. 아래는 $N=5$에 대해 $W_0 - W$를 그려본 그림이다.
$r=0.4$이면 돌연변이가 어떤 $s$를 가지더라도 침입하지 못한다. 즉 이것이 진화적으로 안정한 성비 $r^\ast$이다.
일반적으로는 $r^\ast = \frac{1}{2}(N-1)/N$으로 쓸 수 있다. 극단적으로 $N=1$일 때에는 $r^\ast=0$으로서, 종의 존속을 위한 최소의 수컷만을 낳는 쪽으로 성비가 치우치게 될 것이다.
반수이배체
실험적으로 중요한 말벌 같은 경우, 수정란에서는 암컷이 태어나고 수정되지 않은 알에서는 수컷이 태어나기 때문에 암컷은 두 벌의 염색체를 가지는 이배체, 수컷은 한 벌의 염색체만을 가지는 반수체가 된다.
여기에서는 $R$과 $S$ 중 $S$가 열성인 돌연변이 유전자로서 암컷에 있을 때에 작용한다고 하자. 즉 $RR$이나 $RS$인 암컷은 수컷을 낳을 비율이 $r$이고 $SS$인 암컷은 수컷을 낳을 비율이 $s$이다.
위에서처럼 하나의 패치에 $N$ 마리의 암컷이 알을 낳을 텐데, 돌연변이가 희귀하기 때문에 이 중 $(N-1)$ 마리는 $RR$과 $R$이 만났던 경우이고 나머지 한 마리에 대해서만 돌연변이가 들어올 수도 있다고 한다. 이 마지막 $N$ 번째 알은 $F$인 암컷과 $M$인 수컷이 만나는 다음과 같은 다섯 가지의 가능성이 있다 (암수가 만났더라도 알은 수정이 되지 않아 반수체 수컷이 나올 수도 있고 이것이 위에 적은 $r$이나 $s$로 결정된다): $SS \times S$, $SS \times R$, $RS \times S$, $RS \times R$, 그리고 $RR \times S$. 이 상태들의 수 $x_{F \times M}$이 어떻게 전이해 가는지를 추적하는 것이 관건이다.
- 먼저 $SS \times S$가 하나 있을 때 몇 개의 $SS \times S$가 나올지 생각해보자. 암컷 한 마리당 $K$ 마리의 자식을 낳는다고 하면, 이 패치에서 태어나는 암컷의 수는 $(N-1)(1-r)K + (1-s)K$이고 이 중 $(N-1)(1-r)K$는 $RR$인 암컷, 나머지 $(1-s)K$는 $SS$인 암컷이다. 마찬가지로 수컷의 수는 $(N-1)rK + sK$로서 $(N-1)rK$는 $R$인 수컷, 나머지 $sK$는 $S$인 수컷이다. 따라서 이들 중 다시 $SS \times S$가 나오는 수는 (암컷 중 $SS$의 수) 곱하기 (수컷 중 $S$의 비율$\equiv p$)로서 아래와 같다:
$$(1-s)K \times \frac{sK}{(N-1)rK + sK} = (1-s)K \times p.$$
- $SS \times S$가 하나 있을 때 $SS \times R$은 몇 개가 될까? 이는 위 계산 중 $p$를 $(1-p)$로만 바꾸어주면 된다.
- 그리고 이 패치 안에는 $RR \times R$과 $SS \times S$만 있으므로 여기에서 $RS$인 암컷을 만들어내는 것은 불가능하다.
- 끝으로, $RR \times S$가 되는 수는 $(N-1)(1-r)K \times p$이다.
예를 하나 더 들어서, $RS \times S$에서 $SS \times S$로 전이하는 경우를 생각해보자. 먼저, 태어나는 암컷 중 $SS$인 수는 $\frac{1}{2} K(1-r)$이며 여기에서 $\frac{1}{2}$는 $RS$ 중 $S$가 넘어와야 하기 때문에 붙었다. 태어나는 수컷의 수는 $rKN$일 텐데 이 중 $S$의 숫자는 $\frac{1}{2}rK$이다. 따라서 생겨나는 $SS \times S$의 수는 $$\frac{1}{2}K(1-r) \times \frac{\frac{1}{2}rK}{rKN} = \frac{K(1-r)}{4N}$$ 이다.
이렇게 모든 경우를 고려해보면 다음과 같은 행렬 방정식을 얻으며 $$\begin{pmatrix} x'_{SS\times S}\\ x'_{SS\times R}\\ x'_{RS\times S}\\ x'_{RS\times R}\\ x'_{RR\times S} \end{pmatrix} =(1-r)K \begin{pmatrix} pu & 0 & \frac{1}{4N} & 0 & 0\\ (1-p)u & 0 & \frac{2N-1}{4N} & 0 & 0\\ 0 & pu & \frac{1}{4N} & \frac{1}{4N} & 0\\ 0 & (1-p)u & \frac{2N-1}{4N} & \frac{2N-1}{4N} & 1\\ (N-1)p & (N-1)p & \frac{N-1}{2N} & \frac{2N-1}{4N} & 0 \end{pmatrix} \begin{pmatrix} x_{SS\times S}\\ x_{SS\times R}\\ x_{RS\times S}\\ x_{RS\times R}\\ x_{RR\times S} \end{pmatrix} $$ 이 때 $u \equiv (1-s)/(1-r)$이다.
일반적인 $RR \times R$이 $(1-r)K$만큼씩 늘어날 것이므로, 돌연변이의 침투를 막기 위해서는 모든 $s$에 대해 $()$ 안에 적힌 정사각 행렬의 고유값 크기가 1보다 커서는 안 된다. 이는 원래 군집의 성비가 $r^\ast \equiv (N-1)(2N-1)/[N(4N-1)]$일 때이다.
검증
위 내용의 검증을 위해 이 군집에 두 쌍만이 존재한다고 가정하고 계산을 수행해보자. 먼저 군집에 존재할 수 있는 두 쌍의 경우의 수는 총 21개이고, 각각의 비율을 $x_1,...,x_{21}$이라고 하자.
$$(RRXR)(RRXR) = x_1,\quad (RRXS)(RRXR) = x_2,\quad (RSXR)(RRXR) = x_3,\quad (RSXS)(RRXR) = x_4\\ (SSXR)(RRXR)=x_5,\quad (RSXR)(RRXS)=x_6,\quad (RRXS)(RRXS)=x_7,\quad (RSXR)(RSXR)=x_8\\ (SSXS)(RRXR)=x_9,\quad (RSXS)(RRXS)=x_{10},\quad (SSXR)(RRXS)=x_{11},\quad (RSXS)(RSXR)=x_{12}\\ (SSXR)(RSXR)=x_{13},\quad (SSXS)(RRXS)=x_{14},\quad (SSXS)(RSXR)=x_{15},\quad (RSXS)(RSXS)=x_{16}\\ (SSXR)(RSXS)=x_{17},\quad (SSXR)(SSXR)=x_{18},\quad (SSXS)(RSXS)=x_{19},\quad (SSXS)(SSXR)=x_{20}\\ (SSXS)(SSXS)=x_{21}$$
그리고 이들의 자녀 세대가 무작위 짝짓기를 한다고 가정하고, 자녀 세대에서 나올 수 있는 각 쌍의 수는 다음과 같다.
$$ N_{RRXR} = (1-r)K\left[2x_1+x_2+\frac{9}{8}x_3+ \frac{3}{4}x_4+\frac{3}{8}x_6+\frac{1}{2}x_8+\frac{1}{4}x_{12}+\frac{r}{r+s}\left(x_5+x_9+\frac{1}{4}x_{13}+\frac{1}{4}x_{15}\right)\right]\\ N_{RRXS} = (1-r)K\left[\frac{3}{8}x_3+\frac{1}{4}x_4+\frac{1}{8}x_6+\frac{1}{2}x_8+\frac{1}{4}x_{12}+\frac{r}{r+s}\left(x_5+x_9\right)+\frac{2s+r}{4(s+r)}\left(x_{13}+x_{15}\right)\right]\\ N_{RSXR} = (1-r)K\left[x_2+\frac{3}{8}x_3+\frac{3}{8}x4+\frac{9}{8}x_6+2x_7+\frac{1}{2}x_8+\frac{9}{8}x_{10}+\frac{1}{2}x_{12}+\frac{1}{2}x_{16}+\frac{r}{r+s}\left(x_{11}+x{14}+\frac{1}{4}x_{15}+\frac{1}{4}x_{17}+\frac{1}{4}x_{19}+\right)\right]\\+(1-s)K\frac{r}{r+s}\left[x_5+x_{11}+\frac{1}{2}x_{13}+\frac{1}{2}x_{17}\right]\\ N_{RSXS} = (1-r)K\left[\frac{1}{8}x_3+\frac{1}{8}x_4+\frac{3}{8}x_6+\frac{1}{2}x_8+\frac{3}{8}x_{10}+\frac{1}{2}x_{12}+\frac{1}{2}x_{16}+\frac{s}{r+s}\left(x_{11}+x_{14}\right)+\frac{2s+r}{4(s+r)}\left(x_{13}+x_{15}+x_{17}+x_{19}\right)\right]\\+(1-s)K\left[2x_{18}+x_{20}+\frac{s}{r+s}\left(x_5+x_{11}\right)+\frac{2s+r}{2(s+r)}\left(x_{13}+x_{17}\right)\right]\\ N_{SSXR} = (1-r)K\left[\frac{3}{8}x_4+\frac{3}{8}x_{10}+\frac{1}{4}x_{12}+\frac{1}{2}x_{16}+\frac{r}{4(s+r)}\left(x_{17}+x_{19}\right)\right]+(1-s)K\frac{r}{r+s}\left[x_9+x_{14}+\frac{1}{2}x_{15}+\frac{1}{2}x_{19}\right]\\ N_{SSXS} = (1-r)K\left[\frac{1}{8}x_4+\frac{1}{8}x_{10}+\frac{1}{4}x_{12}+\frac{1}{2}x_{16}+\frac{2s+r}{4(s+r)}\left(x_{17}+x_{19}\right)\right]+(1-s)K\left[x_{10}+2x_{21}+\frac{s}{s+r}\left(x_9+x_{14}\right)+\frac{2s+r}{2(r+s)}\left(x_{15}+x_{19}\right)\right] $$
이 때 전체 쌍의 수를 $N_{tot} = N_{RRXR}+N_{RRXS}+N_{RSXR}+N_{RSXS}+N_{SSXR}+N_{SSXS}$ 이라고 하고 각 쌍의 비율을
$$P_{RRXR} = \frac{N_{RRXR}}{N_{tot}},\enspace P_{RRXS} = \frac{N_{RRXS}}{N_{tot}},\enspace P_{RSXR} = \frac{N_{RSXR}}{N_{tot}},\enspace P_{RSXS} = \frac{N_{RSXS}}{N_{tot}},\enspace P_{SSXR} = \frac{N_{SSXR}}{N_{tot}},\enspace P_{SSXS} = \frac{N_{SSXS}}{N_{tot}}$$
이라고 한다면 자녀 세대에서 특정 두 쌍이 존재할 확률을 다음과 같이 계산할 수 있다.
$$ x'_{1} = P_{RRXR}\times P_{RRXR},\quad x'_{2} = P_{RRXS}\times P_{RRXR},\quad x'_{3} = P_{RSXR}\times P_{RRXR},\quad x'_{4} = P_{RSXS}\times P_{RRXR}\\ x'_{5} = P_{SSXR}\times P_{RRXR},\quad x'_{6} = P_{RSXR}\times P_{RRXS},\quad x'_{7} = P_{RRXS}\times P_{RRXS},\quad x'_{8} = P_{RSXR}\times P_{RSXR}\\ x'_{9} = P_{SSXS}\times P_{RRXR},\quad x'_{10} = P_{RSXS}\times P_{RRXS},\quad x'_{11} = P_{SSXR}\times P_{RRXS},\quad x'_{12} = P_{RSXS}\times P_{RSXR}\\ x'_{13} = P_{SSXR}\times P_{RSXR},\quad x'_{14} = P_{SSXS}\times P_{RRXS},\quad x'_{15} = P_{SSXS}\times P_{RSXR},\quad x'_{16} = P_{RSXS}\times P_{RSXS}\\ x'_{17} = P_{SSXR}\times P_{RSXS},\quad x'_{18} = P_{SSXR}\times P_{SSXR},\quad x'_{19} = P_{SSXS}\times P_{RSXS},\quad x'_{20} = P_{SSXS}\times P_{SSXR}\\ x'_{21} = P_{SSXS}\times P_{SSXS} $$
이로써 자녀 세대의 쌍의 비율 ${x'}$를 부모 세대의 쌍의 비율 ${x}$들로 표현해내었다. 지금 우리는 돌연변이가 희귀한 경우에 대해 관심이 있기 때문에 $x_1$을 제외한 나머지 $x_i$들이 매우 작다고 가정하고 다음과 같이 ${x'}$를 $x_i$에 대해 전개할 것이다.
$$ \begin{cases} x'_1 = f_1(x_1,...,x_{21}) \approx \left.\frac{\partial f_{1}}{\partial x_1}\right\vert_{(1,0,...,0)} (x_1 - 1) + \cdots + \left.\frac{\partial f_{1}}{\partial x_{21}}\right\vert_{(1,0,...,0)} x_{21}\\ x'_2 = f_2(x_1,...,x_{21}) \approx \left.\frac{\partial f_{2}}{\partial x_1}\right\vert_{(1,0,...,0)} (x_1 - 1) + \cdots + \left.\frac{\partial f_{2}}{\partial x_{21}}\right\vert_{(1,0,...,0)} x_{21}\\ \qquad\qquad\cdot\\ \qquad\qquad\cdot\\ \qquad\qquad\cdot\\ x'_{21} = f_{21}(x_1,...,x_{21}) \approx \left.\frac{\partial f_{21}}{\partial x_1}\right\vert_{(1,0,...,0)} (x_1 - 1) + \cdots + \left.\frac{\partial f_{21}}{\partial x_{21}}\right\vert_{(1,0,...,0)} x_{21}\\ \end{cases} $$
이제 이 20×20 행렬의 가장 큰 고윳값을 $r$과 $s$에 따라 그리고, 고윳값이 1보다 작은 영역을 보면 다음을 얻는다.
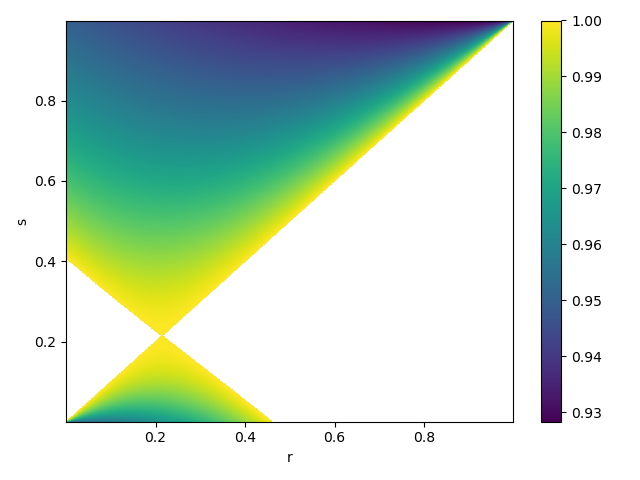
이로써 $N=2$일 때 평형 성비는 $r=0.214$가 됨을 알 수 있다.
그리고 한 쌍이 $(RRXR)$이라고 가정하고 $x'_2,x'_3,x'_4,x'_5,x'_9$를 가지고 5×5 행렬을 써보면 이 행렬이 윗 절의 $$ \begin{pmatrix} pu & 0 & \frac{1}{4N} & 0 & 0\\ (1-p)u & 0 & \frac{2N-1}{4N} & 0 & 0\\ 0 & pu & \frac{1}{4N} & \frac{1}{4N} & 0\\ 0 & (1-p)u & \frac{2N-1}{4N} & \frac{2N-1}{4N} & 1\\ (N-1)p & (N-1)p & \frac{N-1}{2N} & \frac{2N-1}{4N} & 0 \end{pmatrix} $$
와 같음을 확인할 수 있다.
참고문헌
- W. D. Hamilton, Extraordinary Sex Ratios, Science 156, 477–488 (1967).
- P. D. Taylor and M. G. Bulmer, Local Mate Competition and the Sex Ratio, J. Theor. Biol. 86 409–419 (1980).