사회적인 관계를 기술하는 네트워크(social network)에 대해서는, 종종 그 사회를 구성하는 집단 내에서 발생하는 스트레스(social stress, social tension)를 설명할 수 있으며 $\\$ 그를 정량적으로 설명하고자 하는 시도들은 여러 양질의 연구들에 의해서 지속되어 왔다.$\\$ $\\$

관찰 대상이 되는 사회 집단에서 발생하는 스트레스가 상대적으로 높을 경우에는 사회적인 '균형'(balance)이 잘 맞지 않는 경우라고 설명할 수 있고, 그와 반대로 낮은 경우에는 균형이 잘 맞는 경우라고 할 수 있다.$\\$ 이때 Heider의 균형 이론(balance theory)은 위의 문장에서 설명한 내용의 모호함을 줄이며 보다 정량적으로 설명할 수 있도록 하는 이론이다.

Heider 균형 (Heider balance)의 개념을 꽤 이해하기 쉽도록 설명하는 논문의 한 부분을 인용하고자 한다.$\\$ 아래의 그림은 세 명의 사람들 간의 사회적인 관계를 서로 다른 색으로 구별하여 나타낸 것이다.$\\$

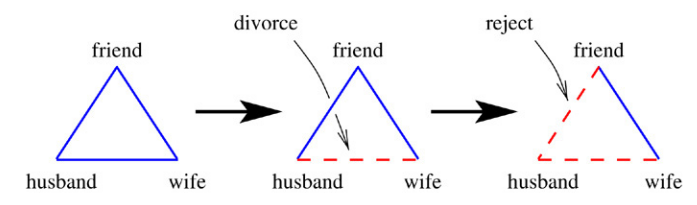$\\$ 파란색의 실선은 '좋은' 관계로서, 값으로 나타내자면 +1 이며, 빨간색의 점선은 '좋지 않은' 관계로서, 마찬가지로 값으로 나타내자면 -1 로 설정할 수 있다.$\\$

각각의 화살표가 의미하는 과정 및 순서는 다음과 같다. $\\$ (1) 서로 배우자의 관계였던 부부와, 남편 및 아내에게 동시에 친구인 사람들이 구성하는 '균형 있는' 삼각형,$\\$ (2) 부부의 이혼에 의해서 배우자였던 둘 사이의 관계는 좋지 않은 관계로 변하게 되어, '균형이 깨진' 삼각형,$\\$ (3) 사회적인 '스트레스'를 줄이기 위해서, 친구가 남편 및 아내 중에서 한 명과의 관계를 좋지 않게 바꾼 결과의 삼각형.$\\$ $\\$ $\\$ 위에서 설명한 '균형 있는 삼각형'의 의미는 '삼각형에서 발생하는 사회적인 스트레스가 없다' 라고 바꾸어 설명할 수도 있다.$\\$ 왜냐하면, 그림의 예에서도 확인할 수 있듯이 모두가 모두에게 좋은 관계로 연결되어 있으므로 해당 삼각형 상에서는 사회적인 스트레스(social stress)가 발생할 이유가 없기 때문이다.$\\$ $\\$ 두 번째 단계의 삼각형의 '균형이 깨진' (imbalanced) 이유도 직관적으로 설명이 가능하다. $\\$ 모두가 친구 및 배우자 관계로서 '좋은 관계'를 가졌던 상태에서 부부 사이가 서로 좋지 않은 관계로 전환 되었으므로 그 둘 모두와 '좋은 관계'를 유지하고 있는 친구의 입장은 다소 불편해진다.$\\$ (논문에서 든 예를 그대로 따라서 설명하자면) 그 친구가 각각의 배우자와 만날 때, 전 배우자에 대한 이야기를 듣게 되면 입장이 불편해지고, 결국 그는 '균형'에 의한 스트레스를 줄이기 위해 둘 중 한 명과의 관계를 좋지 않게 바꾸게 될 것이며$\\$ 그 결과로 세 번째 삼각형과 같은 관계로 배열되어 다시 '균형 있는'(balanced) 삼각형이 된다는 것이다. $\\$ $\\$ 즉, Heider의 균형 이론(balance theory)에 따른 i,j,k 세 사람으로 이루어진 삼각형 균형 (triad balance)을 다음과 같은 값으로 정의할 수 있다.$\\$ $\Phi_{ijk}=J_{ij}J_{jk}J_{ki}$ ($J_{ij}$ : i와 j 사이의 관계, +1 또는 -1) $\\$ 이때, $\Phi_{ijk}=1$ 인 경우가 balanced인 상태이고, $\Phi_{ijk}=-1$ 인 경우는 imbalanced한 상태로서 일반화가 가능하다.

위에서 설명한 대로, 상호간의 관계를 +1 또는 -1인 '2개의 값만을 갖는'(binary) 값으로 설정하는 것이 적절한 경우에는$\\$ Heider의 balance 개념을 이용하여 사회적 네트워크 (social network) 상에서 사회 집단이 두 개 이상의 그룹으로 쪼개어지는 원리를 보다 원활히 이해할 수 있다. $\\$ 이 게시글 맨 하단부의 '참고문헌' 목록 중 'On the Notion of Balance of a Signed Graph'의 제목을 가진 논문을 살펴보면 다음과 같은 정리가 있다.$\\$

“complete signed graph 'G'가 balanced 하다는 것은 $\\$ 'G가 두 부분(two subsets)으로 분할 되고, 동일한 부분 (the same subset) 내의 점(point, 일반적으로 node)들 끼리는 양(positive)의 부호로 연결되며 $\\$ 서로 다른 부분 (the two different subsets) 사이의 점들 끼리는 음(negative)의 부호로 연결'되거나 $\\$ 'G의 모든 점들이 서로 양의 부호로 연결' 되는 경우라는 것과 동치 이다.

후자의 경우와 같이 '모든 연결의 부호가 양수'라면, G에 속하는 임의의 $i,j,k$에 대해서 $\Phi_{ijk}=1$가 만족 되지만,$\\$ 전자의 경우에서도 모든 삼각 구조에서 $\Phi_{ijk}=1$가 만족 될까? $\\$ 이를 시각적으로 이해하기 위해서는 다음의 그림을 살펴볼 수 있다. $\\$ 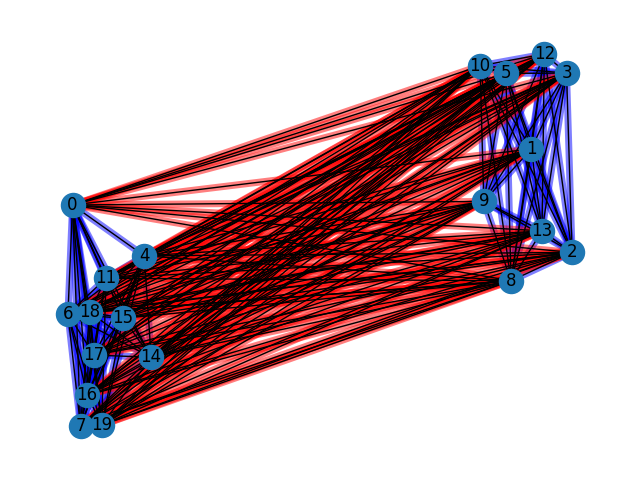$\\$ 위 그림에서 파란색 선(link)은 +1을, 빨간색 선은 -1의 값을 나타낸다.$\\$ 즉, 두 개의 그룹으로 나뉘며 각각의 '그룹 내부'의 점들 사이에는 +1의 선으로만 연결되어있고, '서로 다른 그룹'을 잇는 연결선은 -1의 부호만을 갖는다.$\\$

이 경우, 존재하는 각각의 삼각 구조는 '2개의 부호가 -1, 1개의 부호가 +1인 구조' 이거나$\\$ '모든 부호가 +1인 구조' 만이 존재하므로, 삼각형 균형이 만족 된다는 것을 곧바로 알 수 있다.

• Social balance on networks: The dynamics of friendship and enmity(2006) (T.Antal, P.L.Krapivsky, S.Redner) https://doi.org/10.1016/j.physd.2006.09.028$\\$
• The effect of social balance on social fragmentation (2020) (Tuan Minh Pham, Imre Kondor, Rudolf Hanel and Stefan Thurner) https://doi.org/10.1098/rsif.2020.0752
• Balanced-imbalanced transitions in indirect reciprocity dynamics on networks (2021) (Koji Oishi, Shuhei Miyano, Kimmo Kaski, and Takashi Shimada) https://doi.org/10.1103/PhysRevE.104.024310
• On the Notion of Balance of a Signed Graph(1953) (Frank Harary) https://projecteuclid.org/journals/michigan-mathematical-journal/volume-2/issue-2/On-the-notion-of-balance-of-a-signed-graph/10.1307/mmj/1028989917.full