정의

This is an old revision of the document!

아래는 새로 생성할 예정인 문서들.

Title: 정보 엔트로피

섀넌은 정보량을 표현하기 위해 다음으로 정보 엔트로피를 정의하였다. 임의의 확률 분포 $X=(p_1, ..., p_n)$에서 계산되는 정보량은

\begin{equation} H(X) \equiv H(p_1, ..., p_n) = -\sum_x p_x \log p_x \end{equation}

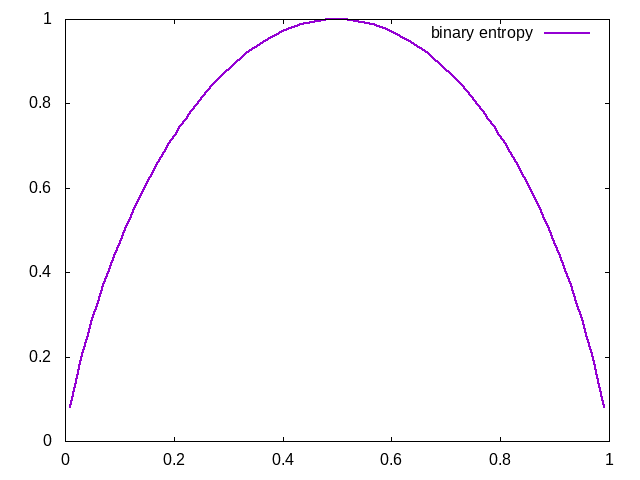
여기서 $\log$는 밑이 2인 로그를 의미한다. $H(X)$가 가질수 있는 양의 범위는 $p_x=[0,1]\,, H(X)=[0,1]$이며, $p_x=0.5$에서 최댓값을 가지는, 대칭인 함수이다. 이 때 $p_x=0$인 경우에서 로그의 정의로 인해 $\log0$에 대해 해석하지 못하는 문제가 있는 데, 이 경우 선형함수가 더 빠르게 값이 줄어들어, $p_x=0$ 이면 $H(X)=0\log0\simeq0$으로 간주한다.

섀넌의 식은 두 가지로 해석할 수 있다.

측정을 한 후 측면에서, “얼마나 많은 정보량을 얻는 가?”
측정을 하기 전 측면에서, “불확정성의 양을 측정”

측정을 하고 나면 결과만을 보고, $H(X)$의 관점에서 생각하면 정보량을 이만큼 얻을 수 있겠다고 생각할 수 있다. 반대로 정보량이 크다는 것은, 어떤 사건이 발생하는 불확실성이 크다는 이야기가 된다.

앞면과 뒷면을 던지는 상황을 생각해보자. 앞면(head)이 발생할 확률을 $p_H$, 뒷면(tail)이 발생할 확률은 $p_T$라고 하자. 두 사건의 확률은 다음으로 가정하자.

\begin{equation} p_H=\frac{1}{4} \qquad p_T=\frac{3}{4} \end{equation}

두 경우만 따지자면, 뒷면이라는 사건이 더 잘 발생할 것으로 보이고, 앞면은 그렇지 않을 것으로 보인다. 실제로도 정보 엔트로피를 계산하면,

\begin{equation} H(p_H)=-\frac{1}{4}\log\frac{1}{4}=1.0 \qquad H(p_T)=-\frac{3}{4}\log\frac{3}{4} \approx 0.811 \end{equation}

으로 앞면에 대한 정보 엔트로피가 더 큰것을 알 수 있다.

먼저 보다 간결한, 이항(binary) 정보 엔트로피를 생각한다.

\begin{equation} H_{\rm bin} = -p\log p -(1-p)\log(1-p) \end{equation}

$H(1/2)$ 에서 최댓값을 가진다.
$H(p)=H(1-p)$

옌센 부등식은 본래 적분의 볼록함수 값과 볼록함수의 적분을 비교하는 부등식으로, 볼록함수 $f$와 지점 $p \in [0,1]$ 에 대해

\begin{equation*} f(px_1-(1-p)x_2) \leq pf(x_1)+(1-p)f(x_2) \end{equation*}

만약 함수 f가 오목함수인 경우, 부등호는 뒤집힌다. 옌센 부등식의 조건으로 인해, 두 개 이상의 확률 분포를 가지는 엔트로피에 대한 특징을 알 수 있다. 이를테면 앞의 동전던지기 예제에서 100원과 500원 동전을 각각 던진다고 생각하자. 동전던지기에 대한 엔트로피는

\begin{equation} H_{\rm flip} = -q\log q -(1-q)\log(1-q) \end{equation}

이고, 100원 동전을 던질 확률 $p_{A}$, 500원 동전을 던질 확률을 $p_{B}$이라고 하면,

\begin{equation*} H(qp_{A}+(1-q)p_{B}) \geq qH(p_{A}) + (1-q)H(p_{B}) \end{equation*}

이 때 이항 엔트로피는 오목함수이므로 부등호가 뒤집혔다.