공동 방법(cavity method)
TAP(Thouless-Anderson-Palmer)방정식은 '셰링턴-커크패트릭 모형'에 대해서 공동 방법(cavity method)으로 유도할 수 있다.
$$ \\ $$ 기본적인 아이디어는, $N$개의 스핀(spin)으로 이루어진 계에서 $N+1$개의 스핀으로 이루어진 계로 변화 시키면서도
그러한 두 계에서 얻는 관측 가능량(observables)이 '열역학적 극한'에서 차이가 없어야 한다는 점을 이용하는 것이다.
$$ \\ $$
국소장 $\tilde{h}_0$
관측 가능량 중 하나로서 '국소적 자화량(local magnetization)'을 $m_0 = \langle S_0 \rangle$라고 표기한다면, 이는 한 곳에 대한 열적 평균(thermal average)을 내린 값이다.
$$ \\ $$ 이때, 원래 $N$개의 스핀으로 이루어진 게에 $S_0$를 추가하는 상황을 생각해보자.
($S_0$는 위치 $0$에 추가된 스핀을 의미하는 관습적인 표기법이다.)
그에 따라 $N+1$개의 스핀으로 이루어진 계로 변화하였다. 그의 국소적 자화량은 $m_0=\langle S_0 \rangle$이다.
$$ \\ $$ 이번 글에서의 최종 목표는, 이러한 국소적 자화량이 TAP 방정식을 만족함을 보이는 것이다.
이어지는 논의에서는 편의상 외부 자기장은 없다고 하여 그에 따라 $h_i=0$이라고 하자.
$$ \\ $$ 국소적 자화량에 대한 평균인 $\langle S_0 \rangle$을 얻기 위해서는, 국소적 스핀에 대한 분포함수 $P(S_0)$를 얻으면 되는데
이를 구하기 위해서는 아래의 국소장(local field)을 먼저 고려해야 한다.
$$ \tilde{h}_0 = \sum_{j} J_{0j}S_j $$
왜냐하면 스핀 $S_0$가 추가되므로 그의 이웃인 스핀 $S_j$들의 상호작용을 고려해야 한다.
따라서 $S_0$와 $\tilde{h}_0 $의 결합 분포(joint distribution) $P(S_0,\tilde{h}_0)$를 구한 후에, 그를 통해 $S_0$와 $\tilde{h}_0$의 열적 평균 값을 구하면 될 것이다.
$$ \\ $$ $S_0$에 의해 스핀 $N$개에서 $N+1$개로 변한다면, 에너지 $E^{(N)}$에서 $E^{(N+1)}$로 다음과 같이 변한다.
$$ S_0 = 1 , \quad E^{(N+1)}=E^{(N)}-\beta \tilde{h}_0 \\ S_0 = -1 , \quad E^{(N+1)}=E^{(N)}+\beta \tilde{h}_0 $$
$$ \\ $$ 즉, 우리가 구하고자 하는 $P(S_0,\tilde{h}_0)$는 다음과 같이 표현될 것이다.
$$ P(S_0,\tilde{h}_0) \propto \ e^{\beta \tilde{h}_0 S_0} P(\tilde{h}_0 \S_0)$$
여기에서 $P(\tilde{h}_0\S_0)$는 $S_0$가 식에 포함되지 않은 확률 분포를 말한다.
더 자세하게 표현하자면, $P(\tilde{h}_0\S_0)$는 ($S_0$가 아닌) $\tilde{h}_0$에 대한 확률 분포의 식이며, $e^{\beta \tilde{h}_0 S_0}$은 $N+1$의 계를 기술하기 위해 $P(\tilde{h}_0\S_0)$에 포함되었다.
이제 $ P(\tilde{h}_0 \S_0)$의 식을 나타낼 수 있다면, 공동 방법(cavity method)의 기본적인 아이디어를 통해서 'TAP 방정식'을 얻는 것이 가능하다.
$$ \\ $$
$P(\tilde{h}_0 \S_0)$
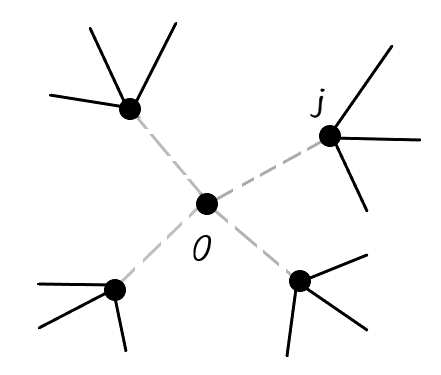
만약 격자 구조가 아래와 같은 베테 격자(Bethe lattice) 구조라면,
$P(\tilde{h}_0 \ S_0)$에 대해 '중심 극한 정리(central limit theorem)'를 적용할 수 있다.
왜냐하면 위치 $0$의 $S_0$에 연결된 각각의 이웃 위치 $j$에 대한 $J_{0j}S_j$는 '$S_0$의 정보가 제외된다면' 서로 독립적이기 때문이다.
(위의 베테 격자 그림에서 $S_0$를 감싸는 '공동(cavity)'을 생각하고 마치 $S_0$가 없는 상황을 떠올리면 보다 이해하기 쉽다.
그 상황에서 스핀의 개수는 $N$개 이다.)
$$ \\ $$ 이때, 서로 다른 위치에 대한 상관관계(correlation)가 약한 '셰링턴-커크패트릭 모형'에 대해서도 이러한 가정을 도입할 수 있다고 하자.
즉, 독립적이고 동일하게 분포된(independent and identically distributed) $J_{0j}S_j$에 대해서
$S_0$가 식에 포함되지 않는 $\tilde{h}_0$의 분포는 ($N$이 증가함에 따라) 가우스 분포(Gaussian distribution)인 것을 알 수 있다.
$$ \\ $$ 즉, 다음과 같은 형태로 표현 가능하다.
$$ P(\tilde{h}_0 \ S_0)=\frac{1}{\sqrt{2\pi V_0}} \exp \left[ -\frac{(\tilde{h}_0 - \langle \tilde{h}_0\rangle _{\0})^2}{2V_0}\right]$$
위의 식에서 $V_0$는 국소장의 분산(variance)이다.
분산 $V_0$를 식으로 표현하면 아래와 같다.
$$
\begin{align}
V_0 &= \langle (\tilde{h}_0)^2\rangle - \langle
\tilde{h}_0 \rangle ^2
\\
&=\sum_{j,k}J_{0j}J_{0k}(\langle S_jS_k\rangle_{\0} \ \ - \ \langle S_j\rangle_{\0} \langle S_k\rangle_{\0} )
\end{align}$$
$$
$$
이때, '셰링턴-커크패트릭 모형'의 분포함수에 주목하자.
$$ P(J_{ij}) = \frac{1}{J}\sqrt{\frac{N}{2\pi}} \exp\left\{ - \frac{N}{2J^2}\left( J_{ij} - \frac{J_0}{N} \right)^2 \right\} $$
위의 식으로부터 $J_{0j}$의 기댓값은 $\frac{J_0}{N}$이며 분산은 $\frac{J^2}{N}$임을 알 수 있다.
또한 $V_0$를 계산할 때, $N(N-1)$개의 서로 상관관계가 없고 (uncorrelated) 무작위적으로 부호를 갖는 (randomly signed) $j\ne k$의 항들의 합은 열역학적 극한인 $N \to \infty$에서 $0$이 된다.
따라서 $N \to \infty$인 경우에는 $V_0=\sum_{j,k}J_{0j}J_{0k}(\langle S_jS_k\rangle_{\0} \ \ - \ \langle S_j\rangle_{\0} \langle S_k\rangle_{\0} )$의 식에서 $j=k$인 경우만이 살아남는다는 것을 알 수 있다.
그 결과는 다음과 같이 표현 된다.
$$ V_0 \approx \sum_j J_{0j}^2(1-\langle S_j \rangle^2 _{\0} \approx \sum_j J_{0j}^2(1-\langle S_j \rangle^2 = \sum_j J_{0j}^2 (1-m_j ^2) $$
이와 같이 국소장의 분산 $V_0$을 얻었으므로 $ P(S_0) \propto \int d \tilde{h}_0 \ e^{\beta \tilde{h}_0 S_0} P(\tilde{h}_0 \S_0)$의 관계를 이용하여 $m_0$를 구하면 된다.
$$ \\ $$
$m_0$
위에서 설명한 식에 따라서 $P(S_0)$는 다음과 같이 표현된다. $$ \begin{align} P(S_0) & \propto \int d \tilde{h}_0 \ \exp[{\beta \tilde{h}_0 S_0}] P(\tilde{h}_0 \S_0) \\ & = \int d\tilde{h}_0 \frac{1}{\sqrt{2\pi V_0}} \exp[{\beta \tilde{h}_0 S_0}] \exp \left[ -\frac{(\tilde{h}_0 - \langle \tilde{h}_0\rangle _{\0})^2}{2V_0}\right]\\ & = \frac{1}{\sqrt{2\pi V_0}} \int d\tilde{h}_0 \exp\left[-\frac{(\tilde{h}_0 - \langle \tilde{h}_0\rangle _{\0})^2}{2V_0} +\beta \tilde{h}_0 S_0 \right] \\ &= \frac{1}{\sqrt{2\pi V_0}} \int d\tilde{h}_0 \exp\Biggl[ -\frac{1}{2V_0}\left(\tilde{h}_0^2 -2\tilde{h}_0\langle \tilde{h_0}\rangle_{\0} +\langle \tilde{h_0}\rangle_{\0}^2 -2V_0\beta S_0 \tilde{h}_0 \right) \Biggr]\\ &=\frac{1}{\sqrt{2\pi V_0}} \int d\tilde{h}_0 \exp\Biggl[ -\frac{1}{2V_0}\Bigl(\tilde{h}_0^2 -2\tilde{h}_0(\langle \tilde{h_0}\rangle_{\0}+V_0\beta S_0) \\ &\qquad \qquad +(\tilde{h}_0\langle \tilde{h_0}\rangle_{\0}+V_0\beta S_0) ^2-(\tilde{h}_0\langle \tilde{h_0}\rangle_{\0}+V_0\beta S_0) ^2 +\langle \tilde{h_0}\rangle_{\0}^2 \Bigr) \Biggr]\\ &=\frac{1}{\sqrt{2\pi V_0}} \int d\tilde{h}_0 \exp\Biggl[ -\frac{1}{2V_0}\Bigl( \tilde{h}_0 -(\langle \tilde{h_0}\rangle_{\0}+V_0\beta S_0)\Bigr)^2\Biggr]\\ &\qquad \qquad \qquad × \exp\Biggl[-\frac{1}{2V_0}\Bigl(-( \langle \tilde{h_0}\rangle_{\0}+V_0\beta S_0) ^2 +\langle \tilde{h_0}\rangle_{\0}^2 \Bigr)\Biggr]\\ &=\frac{1}{\sqrt{2\pi V_0}}\exp\Biggl[-\frac{1}{2V_0}\Bigl(-( \langle \tilde{h_0}\rangle_{\0}+V_0\beta S_0) ^2 +\langle \tilde{h_0}\rangle_{\0}^2 \Bigr)\Biggr] \sqrt{2\pi V_0}) \\ &=\exp\Biggl[-\frac{1}{2V_0}\Bigl(-( \langle \tilde{h_0}\rangle_{\0}+V_0\beta S_0) ^2 +\langle \tilde{h_0}\rangle_{\0}^2 \Bigr)\Biggr] \\ &=\exp\Biggl[ \frac{1}{2V_0}\Bigl( 2 \langle \tilde{h_0}\rangle_{\0}V_0\beta S_0 +(V_0\beta S_0)^2 \Bigr)\Biggr] \\ &=\exp\left[\frac{1}{2V_0}(V_0\beta)^2 \right]\exp\Bigl[ \beta \langle \tilde{h_0}\rangle_{\0} S_0\Bigr] \end{align}$$ 이제 $P(S_0)$가 $\exp\Bigl[ \beta \langle \tilde{h_0}\rangle_{\0} S_0\Bigr] $에 비례한다는 것을 얻었으므로, 아래와 같이 $m_0$룰 계산하자.
$$ \begin{align} m_0 &= \sum_{S_0=\pm 1} \frac{1}{[\exp[\beta \langle \tilde{h_0}\rangle_{\0} \ + \exp[-\beta \langle \tilde{h_0}\rangle_{\0}]]} S_0\exp\bigl[ \beta \langle \tilde{h_0}\rangle_{\0} S_0\bigr] \\ &=\tanh[\beta \langle \tilde{h_0}\rangle_{\0}] \end{align} $$ 여기에서 $\langle \tilde{h_0}\rangle_{\0}$라고 함은 스핀 $N$개에 대한 $\tilde{h}_0$의 평균값이다.
그러므로 $\langle \tilde{h_0}\rangle_{\0}$의 식을, 스핀 $N+1$개에 대한 $\langle \tilde{h_0}\rangle$에 대해서 얻으면 $m_0$를 온전히 표현할 수 있다.
$$ \\ $$ $\langle \tilde{h_0}\rangle_{\0}$이 아닌 $\langle \tilde{h_0}\rangle$ 로서 '$S_0$를 제외 시키지 않은' 경우의 $\tilde{h}_0$의 기대값은 다음과 같이 쓸 수 있다.
$$ \langle \tilde{h}_0 \rangle = \text{Tr}_{S_0} \int d\tilde{h}_0 \tilde{h}_0 P(S_0,\tilde{h}_0) $$
여기에서 (앞서 살펴본) $P(S_0,\tilde{h}_0) \propto e^{\beta\tilde{h}_0 S_0}P(\tilde{h}_0 \ S_0)$를 이용하면
다음과 같은 과정에 의해서 $\langle \tilde{h_0}\rangle$와 $\langle \tilde{h_0}\rangle_{\0}$에 대한 관계식을 얻는다.
$$ \begin{align} \langle \tilde{h}_0 \rangle &\propto \frac{1}{\sqrt{2\pi V_0}} \ \text{Tr}_{S_0} \int d\tilde{h}_0 \tilde{h}_0\exp \Biggl[ -\frac{(\tilde{h}_0 - \langle \tilde{h}_0\rangle _{\0})^2}{2V_0} +\beta\tilde{h}_0 S_0 \Biggr]\\ &= \frac{1}{\sqrt{2\pi V_0}} \text{Tr}_{S_0} \int d\tilde{h}_0 \tilde{h}_0 \exp\Biggl[ -\frac{1}{2V_0}\Bigl( \tilde{h}_0 -(\langle \tilde{h_0}\rangle_{\0}+V_0\beta S_0)\Bigr)^2\Biggr]\\ &\qquad \qquad \qquad × \exp\Biggl[-\frac{1}{2V_0}\Bigl(-( \langle \tilde{h_0}\rangle_{\0}+V_0\beta S_0) ^2 +\langle \tilde{h_0}\rangle_{\0}^2 \Bigr)\Biggr]\\ &=\frac{1}{\sqrt{2\pi V_0}} \exp\left[\frac{1}{2V_0}(V_0\beta)^2 \right] × \\ &\text{Tr}_{S_0} \exp\Bigl[ \beta \langle \tilde{h_0}\rangle_{\0} S_0\Bigr] \int d\tilde{h}_0 \tilde{h}_0 \exp\Biggl[ -\frac{1}{2V_0}\Bigl( \tilde{h}_0 -(\langle \tilde{h_0}\rangle_{\0}+V_0\beta S_0)\Bigr)^2\Biggr]\\ &=\frac{1}{\sqrt{2\pi V_0}} \exp\left[\frac{1}{2V_0}(V_0\beta)^2 \right] ×\\ &\text{Tr}_{S_0}\exp\Bigl[ \beta \langle \tilde{h_0}\rangle_{\0} S_0\Bigr] \int d\tilde{h}_0 \Bigl( \langle \tilde{h_0}\rangle_{\0}+V_0\beta S_0 \Bigr) \exp\Biggl[ -\frac{1}{2V_0}\Bigl( \tilde{h}_0 -(\langle \tilde{h_0}\rangle_{\0}+V_0\beta S_0)\Bigr)^2\Biggr]\\ &= \exp\left[\frac{1}{2V_0}(V_0\beta)^2 \right]\text{Tr}_{S_0} \exp\Bigl[ \beta \langle \tilde{h_0}\rangle_{\0} S_0\Bigr] \Bigl(\langle \tilde{h_0} \rangle_{\0}+V_0\beta S_0 \Bigr) \\ &= \langle \tilde{h_0} \rangle_{\0}+V_0\beta \langle S_0 \rangle \end{align} $$ $$ \begin{align} \therefore \langle \tilde{h_0} \rangle &= \langle \tilde{h_0} \rangle_{\0}+V_0\beta \langle S_0 \rangle \\ &= \langle \tilde{h_0} \rangle_{\0}+V_0\beta m_0 \end{align}$$ 위의 유도 과정에서는 앞서서 계산한 적분 결과를 곧바로 사용하였고, $P(S_0) \propto \exp\left[\frac{1}{2V_0}(V_0\beta)^2 \right]\exp\Bigl[ \beta \langle \tilde{h_0}\rangle_{\0} S_0\Bigr] $임을 적용하여 관계식을 등호로 바꿀 수 있었다.
$$ \\ $$ 이때 '$S_0$를 제외 시키지 않은' 경우에 해당하는 국소장의 기댓값은 $\langle \tilde{h_0}\rangle=\sum_j J_{0j} m_j$이므로
앞서 얻었던 식인 $m_0 = \tanh[\beta \langle \tilde{h_0}\rangle_{\0}]$은, 결론적으로 아래와 같다.
\begin{align} m_0 &= \tanh\left[\beta \left( \langle \tilde{h_0} \rangle - V_0\beta m_0 \right)\right] \\ &= \tanh\left[\beta \left( \sum_j J_{0j} m_j -\beta \sum_j J_{0j}^2 (1-m_j^2)m_0 \right)\right] \end{align}
위의 유도 결과는 TAP 방정식이라고 불린다. $S_0$가 포함 되었으므로, 스핀 $N+1$개에 대한 계를 기술한다.
$$ \\ $$
TAP 방정식의 가정
TAP 방정식은 고온의 영역에서만 옳은 결과를 준다는 한계가 있다.
$$ \\ $$ 왜냐하면, 우리가 유도 과정을 거칠 때에 사용하였던 주된 가정은 $\sum_{j,k} (\langle S_j S_k\rangle - \langle S_j \rangle \langle S_k \rangle)$이
$j \ne k$ 일 때는 $N \to \infty$에서 크게 기여하지 못한다는 가정이었다.
$$ \\ $$ 그러나, 저온의 영역에서는 $N \to \infty$에서도 $j,k$에 대해서 $(\langle S_j S_k\rangle - \langle S_j \rangle \langle S_k \rangle)$가 유한한 값을 가지므로
TAP 방정식이 정확히 옳은 결과를 주지 못한다.
$$ \\ $$
the reaction field of Onsager
TAP 방정식인 다음의 식을 다시 살펴보면
$$ m_0 = \tanh\left[\beta \left( \sum_j J_{0j} m_j -\beta \sum_j J_{0j}^2 (1-m_j ^2)m_0 \right)\right]$$
$-\beta \sum_j J_{0j}^2 (1-m_j ^2)m_0 $의 항은 마치 '추가로 붙게 된 항'처럼 보인다.
사실, 이 항은 '상쇄'의 역할을 하며 중요한 의미를 갖는다.
$$ \\ $$ 자화량 $m_0$는 $j$의 위치에, '내부장(internal field)' $J_{0j}m_0$만큼의 영향을 준다.
그에 따라, 위치 $j$의 자화량 $m_j$는 $\chi_{jj}J_{0j}m_0$만큼 변하게 된다. $\chi_{jj}$는 다음과 같다.
$$ \chi_{jj} = \frac{\partial m_j}{\partial h_j} \Biggl|_{h_j \to 0}=\beta(1-m_j^2)$$ ($\chi$가 자기 감수율(magnetic susceptibility)이며, 그 값은 앞서 분산 $V_0$를 구할 때와 마찬가지의 방식으로 구할 수 있다.)
$$ \\ $$ 이때, 이렇게 변화한 $m_j$의 값에 의해서 $m_0$가 다시 영향을 받게 되는 값은 다음과 같다.
$$ J_{0j} (\chi_{jj}J_{0j}m_0) = \beta J_{0j}^2(1-m_j^2 )m_0$$ 그런데 이것을 발생시킨 $m_j$의 변화는 $m_0$에 의한 것이므로, 이러한 항의 효과는 제거해주어야 한다.
$$ \\ $$ TAP 방정식에서 $-\beta \sum_j J_{0j}^2 (1-m_j ^2)m_0 $의 항이 해당 역할을 적절하게 수행하므로,
'Onsager의 반응장(reaction field)'으로 불린다.
$$ \\ $$
'복제 대칭 해'의 유도
우리가 복제_대칭_해에서 살펴본 결과는 TAP 방정식을 이용해서도 유도가 가능하다.
우선, 상호작용인 $J_{0j}$를 강자성(ferromagnetic)에 대한 항과 난수(random)로 표현되는 항으로 분리하여 아래와 같이 나타내자.
$$ J_{0j} = \frac{J_0}{N} + \frac{J}{\sqrt{N}}z_{0j} $$
여기에서 $z_{0j}$는 가우스 랜덤 변수(Gaussian random variable)로서 평균이 $0$이며 분산을 $1$로 갖는 변수이다.
앞서 얻었던 $ \langle \tilde{h_0} \rangle = \langle \tilde{h_0} \rangle_{\0}+V_0\beta m_0$의 식에 이를 대입하면 다음과 같다.
$$\langle \tilde{h_0} \rangle_{\0} = \frac{J_0}{N}\sum_j m_j + \frac{J}{\sqrt{N}}\sum_j z_{0j}m_j - V_0 \beta m_0 $$
첫번째 항인 $\frac{J_0}{N}\sum_j m_j$는 $J_0 m$과 같으며, $m$은 강자성 질서 맺음 변수(order parameter)이다.
$$ \\ $$ 세번째 항의 역할은 Onsager의 reaction field에서 살펴본 '공동 보정(cavity correction)'의 효과를 주는 것이므로
두번째 항의 $ z_{0j}m_j$가 독립적인 '담금질' 랜덤 변수(indepedent 'quenched' random variable)인 것으로 가정할 수 있도록 한다.
$$ \\ $$ 이를 보다 자세히 설명하자면, $\langle \tilde{h_0} \rangle_{\0}$를 표현하는 식의 의미는 '공동 장'의 평균으로서 $S_0$가 제거된 경우를 보는 것이므로
한 위치 $j$로 부터 발생하는 기여분은 또 다른 $j$로 부터 발생하는 기여분과 서로 간섭하지 않는다.
$$ \\ $$ 따라서 '중심 극한 정리'를 적용할 수 있고, $\sum_j z_{0j}m_j$가 가우스 분포를 따른다고 가정할 수 있다.
즉, 평균은 $0$이고, 그에 따라 분산은 다음과 같이 표현된다.
$$ \sum_j \sum_k [z_{0j}z_{0k}]m_j m_k = \sum_j m_j^2 = N q$$
그러므로 두번째 항은 가우스 담금질 랜덤 변수 $z$를 이용하여 $\sqrt{Nq}z$로서 표현이 가능하다.
$$ \\ $$ 이러한 결과들을 가지고서, $m_0 = \tanh \left(\beta \langle \tilde{h_0}\rangle_{\0} \right)$를 $z$의 분포에 대해서 평균을 내리면
$$ m= \int \text{D}z \tanh (\beta J_0 m + \beta J\sqrt{q}z) $$ 의 결과를 얻고, 이는 '복제 대칭 해'에 대해서 설명된 게시글에서 확인된 식과 같다.
$$ \\ $$
참고문헌
Hidetoshi Nishimori, Statistical Physics of Spin Glasses and Information Processing An Introduction, 2001.
Gino Del Ferraro, Chuang Wang, Dani Martí, and Marc Mézard, Cavity Method: Message Passing from a Physics Perspective, 2014.
Marc Mézard, Giorgio Parisi, and Miguel Ángel Virasoro, Spin Glass Theory and Beyond, 1987.