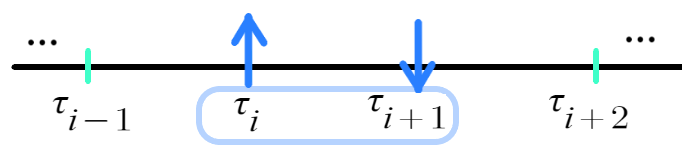
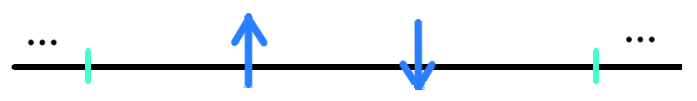ASEP 모형
비대칭 단순 배타 과정 (asymmetric simple exclusion process, ASEP)은 다음과 같은 그림으로 설명 가능하다.
전체 $N$개의 입자들이 총 $L$개의 서로 다른 위치(site)에 존재할 때, 각 위치(site)를 입자가 차지할 수도 있고 그렇지 않을 수도 있는데
어떤 입자가 이미 차지한 자리에는 다른 입자가 올라갈 수 없으므로 '영거리 과정 (zero range process)'과는 달리 '배타 과정'이라고 부른다.
$\\$
각 위치의 입자는 다른 위치로 확률적 이동을 할 수 있고, $q$의 확률로는 바로 왼쪽 위치로 이동하며 $p$의 확률로는 바로 오른쪽 위치로 이동하는 모형이다.
단, '배타 과정'으로서 한 입자가 이동하려는 위치에 이미 다른 입자가 존재할 경우에는 그 위치로 가지 못하므로
임의의 $i$번째 위치에 대한 변수 $n_i$는 $1$ 또는 $0$의 값 만을 가지며, 해당 위치를 차지한 입자가 있다면 $1$, 그렇지 않다면 $0$이다. $\\$
이때 '주기적 경계 조건 (periodic boundary condition, PBC)'을 적용하여 $n_{i+L}=n_i$가 성립되며
$$N=\sum_{i=1} ^L n_i$$ 으로서 전체 입자 개수는 $N$으로 보존된다.
$n_i$에 대응되는 또 다른 변수로, 다음의 '계단 변수 (step variable)'를 정의하는 것이 편리하다. $$ \tau_i \equiv 1-2n_i = \pm 1 $$
계단 변수 $\tau_i$는 $i$번째 위치에 입자가 존재하면 $\tau_i=-1$, 입자가 존재하지 않으면 $\tau_i=+1$이므로 혼동하지 않도록 주의하자.
전체 $L$개 위치에 대해서 임의의 위치 $i$의 $\tau_i$를 다음과 같은 배열(configuration)로 표현할 수 있다.
$$ \boldsymbol{\tau}(\tau_1,...,\tau_L) $$
양자 스핀 사슬
으뜸 방정식
입자들이 특정 확률에 따라 이동하므로, ASEP 모형에 대한 으뜸 방정식(master equation)을
다음과 같은 표기법을 도입하여 얻고자 한다. $$ \boldsymbol{\tau_{i,i+1}'} = (\tau_1, ... , \tau _{i-1} , \color{red} {\tau_{i+1}, \tau_i} , \tau_{i+2}, ... , \tau_L ) $$ 이는 $\boldsymbol{\tau}$에서 $\color{red} i$번째와 $\color{red} {i+1}$번째의 계단 변수가 서로 바뀐 배열을 의미한다.
$\\$
이러한 $\boldsymbol{\tau}$와 $\boldsymbol{\tau_{i,i+1}'}$을 이용하면 으뜸 방정식을 다음과 같이 구할 수 있다.
$$ \begin{align} \dot{P}(\boldsymbol\tau,t) &= p\sum_i \left[ - \frac{(1-\tau_{i})(1+\tau_{i+1})}{4}P(\boldsymbol\tau) +\frac{(1-\tau_{i+1})(1+\tau_{i})}{4}P(\boldsymbol\tau_{i,i+1}')\right] \\ &+q\sum_i \left[ - \frac{(1+\tau_{i})(1-\tau_{i+1})}{4}P(\boldsymbol\tau) +\frac{(1+\tau_{i+1})(1-\tau_{i})}{4}P(\boldsymbol\tau_{i,i+1}')\right] \end{align} $$ 위의 으뜸 방정식 에서 각각의 항을 얻는 방법은 다음과 같이 기술할 수 있다. $\\$
$\\$
(1) $p$에 대한 첫 번째 항
$p\sum_i \left[ -\frac{(1-\tau_{i})(1+\tau_{i+1})}{4}P(\boldsymbol\tau) \right]$ 은 $\tau_{i}=-1$, $\tau_{i+1}=+1$ 일 때만 0이 아닌 값을 가지므로, $\boldsymbol{\tau}$는 각 위치($i$)에 입자가 놓여있으며 한 칸 오른쪽($i+1$)에는 입자가 없는 배열이다.
이때 $p$의 확률에 의해서 $i$번째 위치의 입자가 $i+1$의 위치로 우측 이동을 하게 되어 배열이 바뀐다면
$\tau_{i}=+1$, $\tau_{i+1}=-1$ 의 $\boldsymbol\tau_{i,i+1}'$가 되므로, (1)번 경우에 대해서 $P(\tau,t)$의 기준에서는 음(-)의 변화율에 기여한다.
$\\$
(2) $p$에 대한 두 번째 항
$p\sum_i \left[ \frac{(1-\tau_{i+1})(1+\tau_{i})}{4}P(\boldsymbol\tau_{i,i+1}') \right]$ 은 $\tau_{i}=+1$, $\tau_{i+1}=-1$ 일 때에 0이 아닌 값을 가지며, $\boldsymbol{\tau}$는 각 위치($i$)에 입자가 놓여있지 않으며 한 칸 오른쪽($i+1$)에는 입자가 존재하는 배열이다.
만약 '각 위치($i$)에 입자가 놓여있고 한 칸 오른쪽($i+1$)에는 입자가 없는' 배열인 $\boldsymbol\tau_{i,i+1}'$ 에서 $p$의 확률에 의해 $i$번째 위치의 입자가 $i+1$의 위치로 우측 이동을 하게 되어 배열이 바뀐다면
$\tau_{i}=+1$, $\tau_{i+1}=-1$ 의 $\boldsymbol\tau$가 되므로, (2)번 경우에 대해서 $P(\tau,t)$의 기준에서는 양(+)의 변화율에 기여한다.
$\\$
(3) $q$에 대한 첫 번째 항
$ q\sum_i \left[ -\frac{(1+\tau_{i})(1-\tau_{i+1})}{4}P(\boldsymbol\tau) \right] $ 은 $\tau_{i}=+1$, $\tau_{i+1}=-1$ 일 때에 0이 아닌 값을 가지며, $\boldsymbol\tau$는 각 위치($i$)에 입자가 놓여 있지 않으며 한 칸 오른쪽($i+1$)에는 입자가 있는 배열이다.
이때 $q$의 확률에 의해서 $i+1$번째 위치의 입자가 $i$의 위치로 좌측 이동을 하게 되어 배열이 바뀐다면
$\tau_{i}=-1$, $\tau_{i+1}=+1$ 의 $\boldsymbol\tau_{i,i+1}'$가 되므로, (1)번 경우에 대해서 $P(\tau,t)$의 기준에서는 음(-)의 변화율에 기여한다.
$\\$
(4) $q$에 대한 두 번째 항
$q\sum_i \left[ \frac{(1+\tau_{i+1})(1-\tau_{i})}{4}P(\boldsymbol\tau_{i,i+1}') \right]$ 은 $\tau_{i}=-1$, $\tau_{i+1}=+1$ 일 때에 0이 아닌 값을 가지며, $\boldsymbol\tau_{i,i+1}'$가 각 위치($i$)에 입자가 놓여있으며 한 칸 오른쪽($i+1$)에는 입자가 없는 배열이다.
만약 '각 위치($i$)에 입자가 놓여있지 않고 한 칸 오른쪽($i+1$)에는 입자가 있는' 배열인 $\boldsymbol\tau_{i,i+1}'$ 에서 $q$의 확률에 의해 $i+1$번째 위치의 입자가 $i$의 위치로 좌측 이동을 하게 되어 배열이 바뀐다면
$\tau_{i}=-1$, $\tau_{i+1}=+1$ 의 $\boldsymbol\tau$가 되므로, (2)번 경우에 대해서 $P(\tau,t)$의 기준에서는 양(+)의 변화율에 기여한다.
양자 역학 표기법
'파울리 행렬(Pauli matrices)' $\sigma_i ^{x,y,z}$와 양자 역학의 표기법을 도입해서 $i$번째의 계단 변수를
$2^L$ 차원 힐버트 공간(Hilbert space) 위의 격자 페르미온(lattice fermion) 입자로 간주하면 ($ \{ | \pm, ... ,\pm\rangle \}=\{ | \pm\rangle \otimes ... \otimes | \pm\rangle \}$),
다음과 같이 상태 벡터 (state vector)를 도입할 수 있다. $$ |\Psi(t)\rangle = \sum_{\boldsymbol{\tau}} P(\boldsymbol{\tau},t) | \boldsymbol{\tau}\rangle $$
$\\$
이때, 다음과 같은 해밀토니안 연산자 (Hamiltonian operator)를 정의한다면 $$ \frac{d}{dt} | \Psi \rangle = -H | \Psi \rangle $$ 앞서 얻은 으뜸 방정식을, 양자역학 표기법을 통해서 '고유값 방정식'으로 간주할 수 있게 된다.
즉, 시간에 무관한 정상 상태 (stationary state) $| \Psi_{st}\rangle$는 다음을 만족하며 $$ H | \Psi_{st}\rangle = 0 $$
그에 대응되는 고유값은 $0$이다.
$\\$
해밀토니안 유도
아래의 내용에서, 위에서 살펴본 으뜸 방정식으로 부터 다음의 해밀토니안을 얻는 방법을 소개하기 위해 $$ H=\sum_i\Biggl\{ -p\sigma_i^+ \sigma_{i+1}^--q\sigma_i^-\sigma_{i+1}^+ + \frac{(p+q)}{4}(1-\sigma_i^z\sigma_{i+1}^z) \Biggl\} $$
'올림 연산자'와 '내림 연산자'를 포함한 주요 연산자에 대해서 설명하고자 한다.
올림 연산자, 내림 연산자, 파울리 행렬
우선, 파울리 행렬과 올림/내림 연산자를 행렬 표현으로 다음과 같이 나타낼 수 있다. $$ \sigma^x=\begin{pmatrix} 0 & 1\\ 1 & 0 \end{pmatrix}, \ \sigma^y=\begin{pmatrix} 0 & -i\\ i & 0 \end{pmatrix}, \ \sigma^z=\begin{pmatrix} 1 & 0\\ 0 & -1 \end{pmatrix} \ . $$
$$ \sigma^+=\begin{pmatrix} 0 & 1\\ 0 & 0 \end{pmatrix}, \ \sigma^-=\begin{pmatrix} 0 & 0\\ 1 & 0 \end{pmatrix}\ . $$
ASEP 모형에서 이러한 연산자를 도입하는 이유는, $\tau_i$를 $i$번째 위치에 있는 '스핀의 $z$축 성분'으로 간주하면 해석에 도움을 주기 때문이다.
즉, $\tau_i = +1$과 $\tau_i = -1$을 각각 다음과 같은 행렬 표현으로 나타낼 수 있으며
$$\begin{pmatrix} 1 \\ 0 \end{pmatrix}, \ \begin{pmatrix} 0 \\ 1 \end{pmatrix}\ . $$
올림 연산자 $\sigma_i ^+$를 $\tau_i = -1$에 걸어준 결과와, 내림 연산자 $\sigma_i ^-$를 $\tau_i = +1$에 걸어준 결과는 다음과 같다. $$ \begin{pmatrix} 0 & 1\\ 0 & 0 \end{pmatrix} \begin{pmatrix} 0 \\ 1 \end{pmatrix}=\begin{pmatrix} 1 \\ 0 \end{pmatrix}, \begin{pmatrix} 0 & 0\\ 1 & 0 \end{pmatrix} \begin{pmatrix} 1 \\ 0 \end{pmatrix}=\begin{pmatrix} 0 \\ 1 \end{pmatrix} $$
z축에 대한 파울리 행렬 $\sigma_i ^z$을 $\tau_i = -1$에 걸어준 결과와, $\tau_i = +1$에 걸어준 결과는 다음과 같다. $$ \begin{pmatrix} 1 & 0\\ 0 & -1 \end{pmatrix} \begin{pmatrix} 1 \\ 0 \end{pmatrix}=\begin{pmatrix} 1 \\ 0 \end{pmatrix}, \begin{pmatrix} 1 & 0\\ 0 & -1 \end{pmatrix} \begin{pmatrix} 0 \\ 1 \end{pmatrix}=-\begin{pmatrix} 0 \\ 1 \end{pmatrix} $$ 이를 브라-켓(bra-ket) 표기법을 통해 다음과 같이 표현할 수 있다. $$ \sigma^+|- \rangle \ = \ |+\rangle,\ \sigma^-|+\rangle \ =\ |- \rangle, \\ \sigma^z|+\rangle \ =\ |+\rangle,\ \sigma^z|- \rangle \ =\ -|- \rangle.$$
으뜸 방정식의 각 항을 해밀토니안의 항으로 전환
으뜸 방정식의 각각의 항을 서로 다른 색으로 구분한 뒤, 해밀토니안의 각각의 항에도 마찬가지로 다음과 같이 구분하여 대응 관계를 나타내보자.
$$\begin{align}
\dot{P}(\boldsymbol\tau,t) &= p\sum_i \left[ \color{navy}{-\frac{(1-\tau_{i})(1+\tau_{i+1})}{4}P(\boldsymbol\tau)}
+\color{purple}{ \frac{(1-\tau_{i+1})(1+\tau_{i})}{4}P(\boldsymbol\tau_{i,i+1}')}\right] \\
&+q\sum_i \left[\color{green} {-\frac{(1+\tau_{i})(1-\tau_{i+1})}{4}P(\boldsymbol\tau)}
+\color{red}{\frac{(1+\tau_{i+1})(1-\tau_{i})}{4}P(\boldsymbol\tau_{i,i+1}')}\right]
\end{align}$$
$$
$$
$$H=\sum_i\Biggl\{ \color{purple}{-p\sigma_i^+ \sigma_{i+1}^- }\color{red}{-q\sigma_i^-\sigma_{i+1}^+}
+ \frac{(\color{navy}{p}+\color{green}{q})}{4}(1-\sigma_i^z\sigma_{i+1}^z) \Biggl\}$$
$\\$
($ \frac{d}{dt} | \Psi \rangle = -H | \Psi \rangle $ 의 관계에 의해서 '해밀토니안 연산자'에 붙는 부호는 '시간 미분'과는 반대이다.)
$\\$ 해밀토니안의 첫 번째(보라색) 항과 두 번째(빨간색) 항은 아래와 같이 이해할 수 있다.
$\\$
으뜸 방정식의 보라색 항은 '$p$의 확률에 의해 $\tau_i = +1, \tau_{i+1} = -1$인 (아래와 같은) $\boldsymbol{\tau'_{i,i+1}}$와 관련되며
$\\$ $i$와 $i+1$번 째 스핀의 부호가 서로 뒤바뀌어 다음의 $\boldsymbol{\tau}$가 되는 상황'을 가리키는 것이다.
$\\$
위의 그림처럼, $\boldsymbol{\tau'_{i,i+1}}$는 $i$와 $i+1$번째의 스핀이 이미 뒤바뀌어 있는 배열임에 주의해야 한다.
$\\$ $\\$
이때, 앞서 언급된 아래의 상태를 $\boldsymbol{\tau'_{i,i+1}}$의 배열이 아닌
$i$번째 위치에 -스핀이 있고 $i+1$번째 위치에 +스핀이 있는 $\boldsymbol{\tau}$의 배열로 간주한다면
$\sigma_i ^+ \sigma_{i+1}^-$로서 $\tau_{i+1} = +1$을 $\tau_{i+1} = -1$로 내려주고, $\tau_{i} = -1$을 $\tau_{i} = +1$로 올려줌으로써 아래 상태가 되도록 하고
$p$를 곱셈 하여 해밀토니안의 식에 포함 시킬 수 있으며
이러한 과정을 통해 으뜸 방정식의 $\boldsymbol{\tau'_{i,i+1}}$에 대한 항을, $\boldsymbol{\tau}$와 해밀토니안 연산자에 대한 '고유값 방정식'의 형태로 바꿔줄 수 있다.
으뜸 방정식의 빨간색 항에 대해서도 마찬가지의 방식으로 해석하면 해밀토니안의 두 번째 항에 대응된다는 것을 확인할 수 있다.
$\\$
$(p+q)$와 $\sigma_i^z \sigma_{i+1}^z$에 연관된 해밀토니안의 세 번째 항을 곧바로 이해하는 것은 녹록지 않으므로
해당 항의 상호적인 대응 관계가 $L=4, N=2$의 예에 대해서 성립 되는지 확인 해보자.
$\\$
$L=4, N=2$ (행렬 성분으로 비교)
4칸 중에서 입자가 존재하는 칸을 O, 존재하지 않는 칸을 X 로 표기하면, 가령 OOXX는 $i=1,2$에 입자가 있고 $i=3,4$에 입자가 없는 ($N=2$) 배열을 의미하는 것으로 표기하겠다.
이번 예에서 가능한 배열은 OOXX, OXOX, OXXO, XOOX, XOXO, XXOO로 총 ${4 \choose 2} = 6$가지 이다.
$\\$ $\\$
이때, 으뜸 방정식의 $\dot{P}(\boldsymbol\tau,t)$와 $P(\boldsymbol\tau,t)$의 관계를 다음과 같은 행렬 형식으로 표현할 수 있다.
$$ \frac{d}{dt} \begin{pmatrix} P(\text{OOXX}) \\ P(\text{OXOX}) \\ P(\text{OXXO}) \\ P(\text{XOOX}) \\ P(\text{XOXO}) \\ P(\text{XXOO}) \end{pmatrix} = \begin{pmatrix} -1 & q & 0 & 0 & p & 0 \\ p & -2 & q & q & 0 & p \\ 0 & p & -1 & 0 & q & 0 \\ 0 & p & 0 & -1 & q & 0 \\ q & 0 & p & p & -2 & q \\ 0 & q & 0 & 0 & p & -1 \end{pmatrix} \begin{pmatrix} P(\text{OOXX}) \\ P(\text{OXOX}) \\ P(\text{OXXO}) \\ P(\text{XOOX}) \\ P(\text{XOXO}) \\ P(\text{XXOO}) \end{pmatrix} $$
여기서 각각의 $P$는 해당 배열로 자리 잡을 확률을 의미하며, 가령 $P(\text{OXOX})$는 $i=1,i=3$에는 입자가 있고 $i=2,i=4$에는 입자가 없는 배열의 확률이다.
$$ \\ $$ 첫($1$)번 째 배열인 $\text{OOXX}$에서 $i=2$에 위치한 입자가 $p$의 확률로 $i=3$으로 이동한다면 두($2$)번 째 배열인 $\text{OXOX}$로 바뀌므로, 성분 $(2,1)$ 값이 $p$이며
다섯($5$)번 째 배열인 $\text{XOXO}$에서 $i=2$에 위치한 입자가 (주기적 경계 조건에 의해) $q$의 확률로 $i=1$으로 이동한다면 세($3$)번 째 배열인 $\text{OXXO}$로 바뀌므로, 성분 $(3,5)$ 값이 $q$이다.
그리고 여섯($6$)번 째 배열인 $\text{XXOO}$에서 좌측 또는 우측 이동하여 네($4$)번 째 배열인 $\text{XOOX}$로 바뀔 수 없으므로, 성분 $(4,6)$ 값이 $0$이다.
$$ \\ $$ 가능한 경우에 대한 확률을 전부 합하면 $1$이 되어야 하므로, $\frac{dP}{dt}$에 대응하는 행렬의 각 행과 열 성분의 합은 $0$이기 때문에
대각성분 $(1,1),(2,2),(3,3),(4,4),(5,5),(6,6)$은 각각 $-1,-2,-1,-1,-2,-1$로 채울 수 있다.
이때, 아래의 해밀토니안과 위에서 볼 수 있는 행렬이 잘 대응되는지 확인하기 위해서
$$H=\sum_{i=1}^L \Biggl\{ -p\sigma_i^+ \sigma_{i+1}^- -q\sigma_i^-\sigma_{i+1}^+ + \frac{(p+q)}{4}(1-\sigma_i^z\sigma_{i+1}^z) \Biggl\} \\ = H_1 + H_2 + H_3 + H_4 $$ 로 두어서 각각의 $H_i$의 행렬 표현을 아래의 과정을 통해 얻고 $H=-\frac{d}{dt}$로 비교하려고 한다.
$$ \\ $$
(1) $H_1$
$$H_1= \Biggl\{ -p\sigma_1^+ \sigma_{2}^- -q\sigma_1^-\sigma_{2}^+ + \frac{(p+q)}{4}(1-\sigma_1^z\sigma_{2}^z) \Biggl\} $$
위의 $H_1$은 $1$번째와 $2$번째 위치에만 관련된 연산자로서, 가령 $2$번째 배열인 $P(\text{OXOX})$에 대해서는 (개념적인 표기법을 사용하자면) 다음과 같은 결과를 준다.
$$ H_1 | \boldsymbol{\tau_2} \rangle = -p | \boldsymbol{\tau_4} \rangle + \frac{(p+q)}{2} | \boldsymbol{\tau_2} \rangle $$
$\text{OXOX}$의 배열을 갖는 상태를 $| \boldsymbol{\tau_2} \rangle$ 로 표현했으며, $4$번째인 $\text{XOOX}$의 배열을 갖는 상태를 $| \boldsymbol{\tau_4} \rangle$ 로 표현하였다.
위의 식을 볼 때 주의해야 할 점은 올림연산자 / 내림연산자는 $n_i$(입자 기준)가 아닌 $\tau_i$(계단 변수)에 작용해준다는 부분이다.
$$ \\ $$ 즉, 입자가 $\color{red}{OX}\text{OX}$에서 $p$의 확률로 이동하여 $\color{red}{XO}\text{OX}$의 배열이 될 경우, 이는 (계단 변수의 관점에서는) $\color{red}{-+}-+$에서 $p$의 확률로 이동하여 $\color{red}{+-}-+$가 된 것임을 고려해야 한다.
따라서 $\text{OXOX}$의 배열에서 $\text{XOOX}$가 되었다면 그는 $i=1$에는 '올림 연산자'를, $i+1=2$에는 '내림 연산자'를 적용하여 얻은 것이다.
그러므로, $H_1$의 $2$행 $2$열의 성분은 $\frac{1}{2}$이며 $4$행 $2$열의 성분은 $-p$이다.
$$ \\ $$ 이러한 방식으로 $H_1$의 모든 성분들을 구해준 결과는 다음과 같다.
$$ H_1 \begin{pmatrix} P(\text{OOXX}) \\ P(\text{OXOX}) \\ P(\text{OXXO}) \\ P(\text{XOOX}) \\ P(\text{XOXO}) \\ P(\text{XXOO}) \end{pmatrix}=\begin{pmatrix} {0} & {0} & {0} & {0} & {0} & {0} \\ {0} & {\frac{1}{2}} & {0} & {-q} & {0} & {0} \\ {0} & {0} & {\frac{1}{2} } & {0} & {-q} & {0} \\ {0} & {-p} & {0} & {\frac{1}{2}} & {0} & {0} \\ {0} & {0} & {-p} & {0} & {\frac{1}{2}} & {0} \\ {0} & {0} & {0} & {0} & {0} & {0} \end{pmatrix} \begin{pmatrix} P(\text{OOXX}) \\ P(\text{OXOX}) \\ P(\text{OXXO}) \\ P(\text{XOOX}) \\ P(\text{XOXO}) \\ P(\text{XXOO}) \end{pmatrix} $$
$ \\ $
(2) $H_2$
$$H_2= \Biggl\{ -p\sigma_2^+ \sigma_{3}^- -q\sigma_2^-\sigma_{3}^+ + \frac{(p+q)}{4}(1-\sigma_2^z\sigma_{3}^z) \Biggl\} $$ 이번의 경우는 $2$번째와 $3$번째 위치에만 관련된 $H_2$를, (앞서 적용한 것과 동일한 방식으로) 다음과 같이 구할 수 있다.
$$ H_2 \begin{pmatrix} P(\text{OOXX}) \\ P(\text{OXOX}) \\ P(\text{OXXO}) \\ P(\text{XOOX}) \\ P(\text{XOXO}) \\ P(\text{XXOO}) \end{pmatrix}=\begin{pmatrix} {\frac{1}{2}} & {-q} & {0} & {0} & {0} & {0} \\ {-p} & {\frac{1}{2}} & {0} & {0} & {0} & {0} \\ {0} & {0} & {\frac{1}{2} } & {0} & {0} & {0} \\ {0} & {0} & {0} & {0} & {0} & {0} \\ {0} & {0} & {0} & {0} & {\frac{1}{2}} & {-q} \\ {0} & {0} & {0} & {0} & {-p} & {\frac{1}{2}} \end{pmatrix} \begin{pmatrix} P(\text{OOXX}) \\ P(\text{OXOX}) \\ P(\text{OXXO}) \\ P(\text{XOOX}) \\ P(\text{XOXO}) \\ P(\text{XXOO}) \end{pmatrix} $$
$ \\ $
(3) $H_3$
$$H_3= \Biggl\{ -p\sigma_3^+ \sigma_{4}^- -q\sigma_3^-\sigma_{4}^+ + \frac{(p+q)}{4}(1-\sigma_3^z\sigma_{4}^z) \Biggl\} $$ 마찬가지로, 이번에는 $3$번째와 $4$번째 위치에만 관련된 $H_3$를 다음과 같이 구할 수 있으며
$$ H_3 \begin{pmatrix} P(\text{OOXX}) \\ P(\text{OXOX}) \\ P(\text{OXXO}) \\ P(\text{XOOX}) \\ P(\text{XOXO}) \\ P(\text{XXOO}) \end{pmatrix}=\begin{pmatrix} {0} & {0} & {0} & {0} & {0} & {0} \\ {0} & {\frac{1}{2}} & {-q} & {0} & {0} & {0} \\ {0} & {-p} & {\frac{1}{2} } & {0} & {0} & {0} \\ {0} & {0} & {0} & {\frac{1}{2}} & {-q} & {0} \\ {0} & {0} & {0} & {-p} & {\frac{1}{2}} & {0} \\ {0} & {0} & {0} & {0} & {0} & {0} \end{pmatrix} \begin{pmatrix} P(\text{OOXX}) \\ P(\text{OXOX}) \\ P(\text{OXXO}) \\ P(\text{XOOX}) \\ P(\text{XOXO}) \\ P(\text{XXOO}) \end{pmatrix} $$
$ \\ $
(4) $H_4$
$$H_4= \Biggl\{ -p\sigma_4^+ \sigma_{1}^- -q\sigma_4^-\sigma_{1}^+ + \frac{(p+q)}{4}(1-\sigma_4^z\sigma_{1}^z) \Biggl\} $$ 마지막으로, $4$번째와 $1$번째 위치에만 관련된 $H_4$를 다음과 같이 구할 수 있다.
$$ H_4 \begin{pmatrix} P(\text{OOXX}) \\ P(\text{OXOX}) \\ P(\text{OXXO}) \\ P(\text{XOOX}) \\ P(\text{XOXO}) \\ P(\text{XXOO}) \end{pmatrix}=\begin{pmatrix} {\frac{1}{2}} & {0} & {0} & {0} & {-p} & {0} \\ {0} & {\frac{1}{2}} & {0} & {0} & {0} & {-p} \\ {0} & {0} & {0} & {0} & {0} & {0} \\ {0} & {0} & {0} & {0} & {0} & {0} \\ {-q} & {0} & {0} & {0} & {\frac{1}{2}} & {0} \\ {0} & {-q} & {0} & {0} & {0} & {\frac{1}{2}} \end{pmatrix} \begin{pmatrix} P(\text{OOXX}) \\ P(\text{OXOX}) \\ P(\text{OXXO}) \\ P(\text{XOOX}) \\ P(\text{XOXO}) \\ P(\text{XXOO}) \end{pmatrix} $$
$ \\ $
결과로 얻은 행렬 $H_1,H_2,H_3,$ 그리고 $H_4$를 (프로그래밍 언어 등을 이용해서) 전부 합하여 $H$를 다음과 같이 얻을 수 있는데
$$ \begin{pmatrix} {1} & {-q} & {0} & {0} & {-p} & {0} \\ {-p} & {2} & {-q} & {-q} & {0} & {-p} \\ {0} & {-p} & {1} & {0} & {-q} & {0} \\ {0} & {-p} & {0} & {1} & {-q} & {0} \\ {-q} & {0} & {-p} & {-p} & {2} & {-q} \\ {0} & {-q} & {0} & {0} & {-p} & {1} \end{pmatrix} $$
이는, 앞서 으뜸 방정식의 다음과 같은 형태에서 볼 수 있는 행렬의 모든 성분에 $(-1)$을 곱해준 것과 같으므로
$$ \frac{d}{dt} \begin{pmatrix} P(\text{OOXX}) \\ P(\text{OXOX}) \\ P(\text{OXXO}) \\ P(\text{XOOX}) \\ P(\text{XOXO}) \\ P(\text{XXOO}) \end{pmatrix} = \begin{pmatrix} -1 & q & 0 & 0 & p & 0 \\ p & -2 & q & q & 0 & p \\ 0 & p & -1 & 0 & q & 0 \\ 0 & p & 0 & -1 & q & 0 \\ q & 0 & p & p & -2 & q \\ 0 & q & 0 & 0 & p & -1 \end{pmatrix} \begin{pmatrix} P(\text{OOXX}) \\ P(\text{OXOX}) \\ P(\text{OXXO}) \\ P(\text{XOOX}) \\ P(\text{XOXO}) \\ P(\text{XXOO}) \end{pmatrix} $$
$L=4,N=2$의 예를 통해 다음의 해밀토니안이 으뜸 방정식과 잘 대응됨을 알 수 있다.
$$ H=\sum_i\Biggl\{ -p\sigma_i^+ \sigma_{i+1}^--q\sigma_i^-\sigma_{i+1}^+ + \frac{(p+q)}{4}(1-\sigma_i^z\sigma_{i+1}^z) \Biggl\} $$
$$ \\ $$
$H$의 식에서 음($-$)의 부호에 해당하는 항은 으뜸 방정식에서는 양($+$)의 부호 이므로 $P(\boldsymbol{\tau})$에 대해 '양의 기여'를 하지만
$H$의 식에서 양($+$)의 부호에 해당하는 항은 으뜸 방정식에서는 음($-$)의 부호 이므로 $P(\boldsymbol{\tau})$에 대해 '음의 기여'를 한다.
이를 통해, $H$의 행렬 표현에서의 대각 성분이 양의 기여분(in-flux)을 상쇄하는 음의 기여분(out-flux)을 준다는 것을 확인할 수 있다.
$$ \\ $$
참고 문헌
Jae Dong Noh, Exactly Solvable Many-Body Stochastic Processes, 2014.