개요
섀넌-나이키스트 표본화 정리(Shannon-Nyquist sampling theorem)에 의하면, 신호의 최대 주파수가 B일 때 이를 온전히 재구성하려면 2B 이상의 주파수로 표본을 추출해야 한다.그런데 우리가 보는 대부분의 신호는 큰 패턴이 중요한 역할을 하므로 주파수 밀도 측면에서 희박(sparse)하고, 이를 이용하면 섀넌-나이키스트 표본화 정리가 요구하는 것보다 적은 수의 표본으로도 신호를 재구성할 수 있다. 이러한 아이디어는 Candès, Romberg, and Tao (2006)에 의해 정식화되었고 압축 센싱(compressed sensing)이라 불리고 있다.
기본적인 설명
길이 $N$인 '희박한' 신호 $\mathbf{x}$가 미지수로서 있다. $k\times N$의 '관찰' 행렬 $A$를 곱하자. 이 행렬의 원소는 난수로 주어져 있고 $k \ll N$이라고 가정한다. 그 곱의 결과로 $k$ 차원 벡터 $\mathbf{y} = A \mathbf{x}$를 관찰 결과로 가지고 있다.
$A$와 $\mathbf{y}$만을 가지고 미지수 $\mathbf{x}$를 복원하는 것은 불가능해 보인다. $\mathbf{y}=A\mathbf{x}$를 만족하는 $\mathbf{x}$가 무수히 많기 때문이다. 하지만 그러한 $\mathbf{x}$ 중에서 가장 '희박한' 것, 구체적으로는 $\sum_i |x_i|$를 최소화하는 $\mathbf{x}$를 택하면 원래의 $\mathbf{x}$를 상당히 잘 복원해낼 수 있다.
코드 구현
아래는 참고문헌 항목 중 codeproject.com에 있는 Matlab 코드를 python으로 옮긴 것이다.
from __future__ import print_function,division from numpy import zeros,dot,transpose from numpy.random import normal,choice from pylab import plot,show from l1eq_pd import l1eq_pd # Initialize constants and variables N = 256 # length of signal P = 5 # number of non-zero peaks K = 64 # number of measurements to take x = zeros(N,float) # original signal (P-sparse) # Generate signal with P randomly spread values peaks = choice(N, P, replace=False) x[peaks] = normal(0.0, 1.0, P) # Obtain K measurements A = normal(0.0, 1.0, (K,N)) y = dot(A,x) # Perform Compressed Sensing recovery x0 = dot(transpose(A), y) xp = l1eq_pd(x0, A, [], y) plot(x) show() plot(xp-x) show()
신호의 길이는 $N=256$인데 이 중 $P=5$개 지점에서만 0이 아닌 값을 가진다. 이 신호는 그런 의미에서 '희박'하다. $K=64$는 관찰의 횟수로서 $N$의 1/4에 불과하다. choice 명령을 써서 5개의 점을 임의로 골라내고 그 곳들의 값을 정규(normal) 분포로부터 결정한다.
관찰 행렬 $A$도 정규 분포로부터 만든 다음, 관찰 결과인 $\mathbf{y}=A\mathbf{x}$를 만들어낸다. 이제 $\mathbf{x}$를 모른다고 가정한 채, $A$와 $\mathbf{y}$로부터 신호를 복원해낸다. 여기에서 절대값 합의 최소화를 위해 쓰인 l1eq_pd라는 함수는 아래 페이지에서 내려받을 수 있다: https://github.com/nikcleju/pyCSalgos
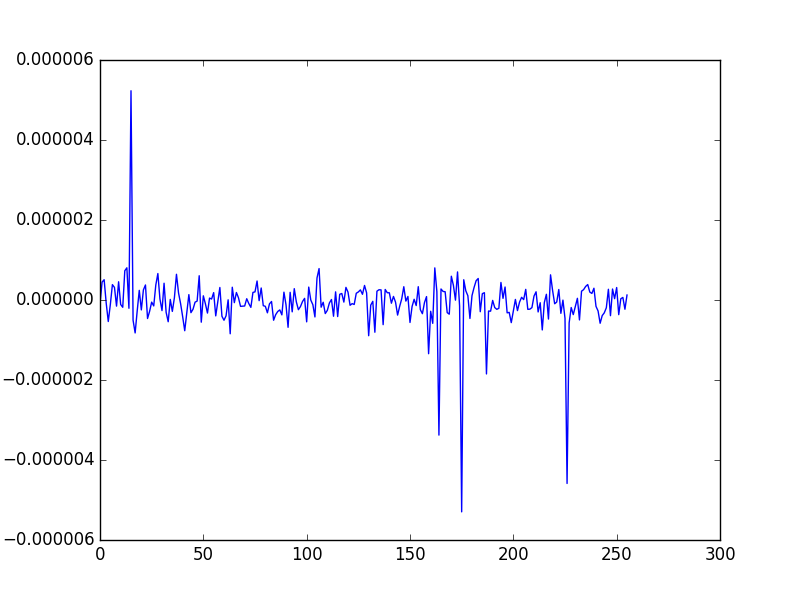
실행 결과는 다음과 같다. 첫 번째 그림은 원래 신호를, 두 번째 그림은 복원된 신호와 원래 신호의 차이를 보여준다. 그 차이는 매우 작다.

푸리에 공간에서 희박한 신호
이 예는 참고문헌 항목 중 pyrunner.com의 내용으로부터 일부를 수정하여 가져온 것이다. 실공간 상에서는 조밀하지만 실제로는 몇 개의 주파수만이 중요한 신호를 생각해보자. 예컨대 다음과 같은 신호는 단 2개의 주파수 성분만을 지닌다: $$x = \sin(10 \pi t) + \sin (54 \pi t).$$ 이산 사인 변환(discrete sine transform, DCT)를 통해 이 신호를 푸리에 공간으로 옮기고 압축 센싱을 실행한 다음 역변환을 할 것이다. 그런데 앞의 코드를 재활용하기 위해 푸리에 변환을 행렬 곱 형태로 표현하면 편리하다 (계산 시간을 생각하면 비효율적인 선택일 것이다): $$\tilde{x} \equiv \mathcal{F}[x] = \Psi \mathbf{x},$$ $$x \equiv \mathcal{F}^{-1}[\tilde{x}] = \Psi^{-1} \tilde{\mathbf{x}}.$$ 이 떄 $x$는 원래 신호, $\tilde{x}$는 그것의 푸리에 변환($\mathcal{F}$) 결과이고 굵은 글씨로 적은 것은 신호를 벡터로서 적은 것을 의미한다. $\Psi$가 푸리에 변환의 역할을 해주는 행렬이다.
코드는 다음처럼 작성할 수 있다.
from __future__ import print_function,division from math import pi from numpy import sin,dot,transpose,identity,linspace from numpy.random import choice from pylab import plot,show from l1eq_pd import l1eq_pd from scipy.fftpack import dst,idst # Initialize constants and variables n = 600 # length of signal m = 50 # number of measurements to take # Generate signal with P randomly spread sinusoids t = linspace(0,1,n) x = sin(10*pi*t) + sin(54*pi*t) # Orthonormal basis matrix Psi = dst(identity(n), norm='ortho', axis=0) Psi_inv = idst(identity(n), norm='ortho', axis=0) xt = dot(Psi,x) # Extract small sample of signal ri = choice(n, m, replace=False) ri.sort() t2, x2 = t[ri], x[ri] plot(t,x,'b') plot(t2,x2, 'r.') show() A = Psi_inv[ri] # sensing matrix y = dot(A,xt) # measured values # Perform Compressed Sensing recovery x0 = dot(transpose(A), y) X_hat = l1eq_pd(x0, A, [], y) x_rec = dot(Psi_inv,X_hat) # IFFT of X_hat(f) plot(x) plot(x_rec, ".") show()
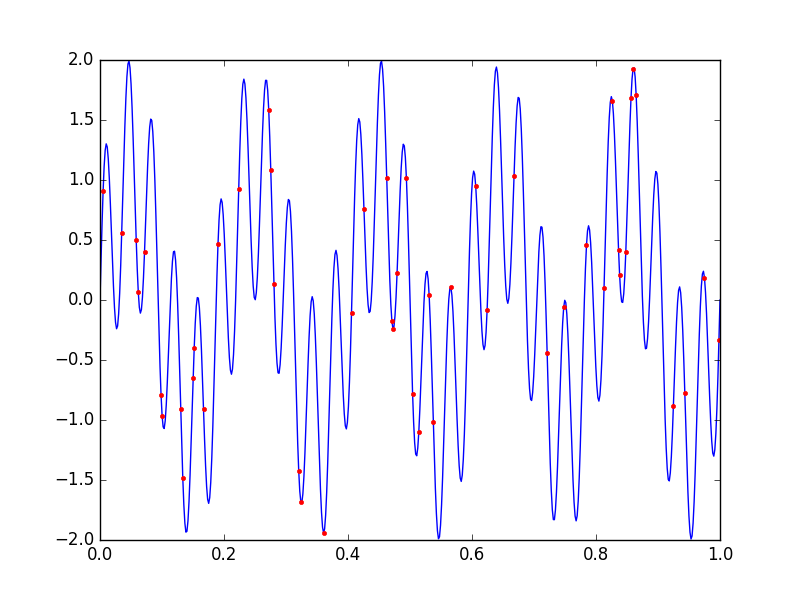
코드의 실행 결과는 아래 그림들처럼 나온다.
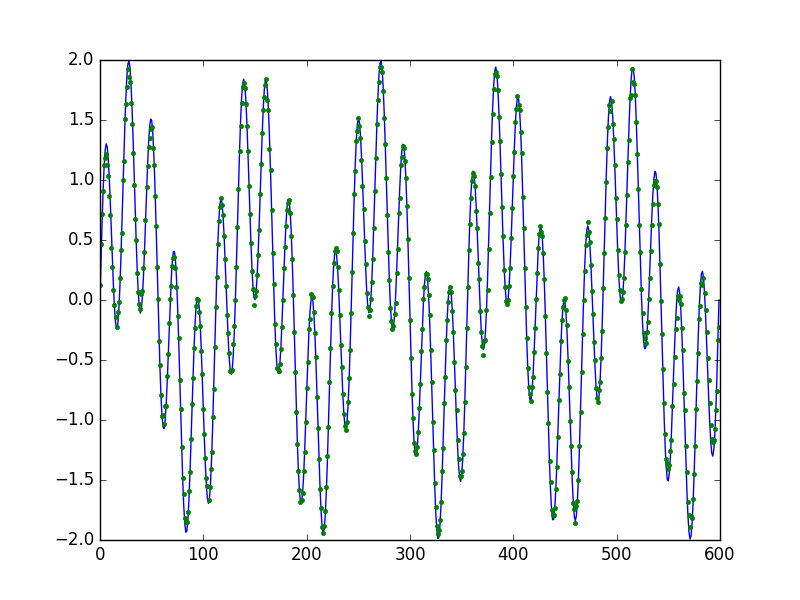
첫 번째 그림은 원래 신호와 그 신호를 추출하기 위해서 무작위로 고른 위치들을 보여준다. 두 번째 그림은 원래 신호(실선)와 복원된 신호(점)를 보여주고 있다. 새넌-나이키스트 정리에서 요구하는 것보다 적은 수의 점을 추출했음에도 불구하고 복원된 신호는 원래 신호와 상당히 가깝다.
통계물리적 접근
2012년, L1 norm에 기반한 방법보다 더 적은 데이터를 가지고도 신호를 복원하는 방법이 개발되었다 [Krzakala et al., PRX 2, 021005 (2012)].