이 모형의 해밀토니안은 다음처럼 정의된다: \begin{equation} H = - \sum_{i<j} J_{ij} S_i S_j - h \sum_i S_i. \end{equation} 이 때 스핀 $i$와 $j$ 사이 상호작용을 나타내는 $J_{ij}$는 다음의 확률 밀도함수로부터 가져온다. \begin{equation} P(J_{ij}) = \frac{1}{J}\sqrt{\frac{N}{2\pi}} \exp\left\{ - \frac{N}{2J^2}\left( J_{ij} - \frac{J_0}{N} \right)^2 \right\} \end{equation} 이 모형의 평형통계적 성질을 알아보려고 한다. 기본 계산은 평균장 이론을 따라가되, 무질서평균(disorder average)을 취하기 위해 무작위장 이징 모형에서처럼 복제(replica) 트릭을 사용할 것이다.

아래 식의 좌변에서 $Z_n$을 감싸고 있는 꺽쇠는 무질서평균을 뜻하며, $\alpha, \beta, \gamma, \delta, \ldots$의 그리스 문자들은 복제본을 가리키는 인덱스들이다. \begin{align} \left[ Z^n \right] &= \int \left[ \prod_{i<j} dJ_{ij} P\left( J_{ij} \right) \right] \text{Tr}_n \exp \left[ \beta \sum_{i<j} J_{ij} \sum_{\alpha = 1}^n S_{i}^{\alpha} S_{j}^{\alpha} + \beta h \sum_{i=1}^N \sum_{\alpha = 1}^{n} S_{i}^{\alpha} \right] \\ &= \text{Tr}_n \int \begin{pmatrix} dJ_{12} P(J_{12}) & \times dJ_{13} P(J_{13}) & \times \cdots & \times dJ_{1n} P(J_{1n}) \\ & \times dJ_{23} P(J_{23}) & \times \cdots & \times dJ_{2n} P(J_{2n}) \\ & & \ddots & \vdots \\ & & & \times dJ_{n-1,n} P(J_{n-1,n}) \end{pmatrix} \\ &\exp\left[ \beta \sum_{\alpha = 1}^n \left( J_{12}S_{1}^{\alpha} S_{2}^{\alpha} + J_{13}S_{1}^{\alpha} S_{3}^{\alpha} + \cdots + J_{23}S_{2}^{\alpha} S_{3}^{\alpha} + \cdots + J_{ij}S_{i}^{\alpha}S_{j}^{\alpha} + \cdots \right) + \beta h \sum_{\alpha = 1}^{n} \left( S_{1}^{\alpha} + S_{2}^{\alpha} + \cdots + S_{N}^{\alpha} \right) \right] \end{align} 여기서 $\text{Tr}_n$은 복제본들의 모든 가능한 스핀 배열(configuration)들에 대한 대각합이다. 먼저 $J_{ij}$에 대한 적분을 할 텐데, 식을 조금 더 읽기 편하게끔 만들기 위해 $X \equiv \sum_{\alpha = 1}^n S_{i}^{\alpha}S_{j}^{\alpha}$로 둔다. \begin{align} &\int dJ_{ij} \ P(J_{ij}) \exp\left[ \beta J_{ij} \sum_{\alpha = 1}^n S_{i}^{\alpha}S_{j}^{\alpha} \right] \\ &= \int dJ_{ij} \ \frac{1}{J}\sqrt{\frac{N}{2\pi}} \exp\left[ -\frac{N}{2J^2}\left( J_{ij} - \frac{J_0}{N} \right)^2 + \beta J_{ij} X \right] \\ &= \frac{1}{J}\sqrt{\frac{N}{2\pi}} \int dJ_{ij} \ \exp\left[ -\frac{N}{2J^2}\left( J_{ij}^2 - \frac{2J_0}{N}J_{ij} + \frac{J_0^2}{N^2} \right) + \beta J_{ij} X \right] \\ &= \frac{1}{J}\sqrt{\frac{N}{2\pi}} \int dJ_{ij} \ \exp\left[ -\frac{N}{2J^2}\left[ J_{ij} - \frac{J^2}{N} \left( \frac{J_0}{J^2} + \beta X \right) \right]^2 + \frac{\beta X J_0}{N} + \frac{J^2}{2N}\beta^2 X^2 \right] \end{align} 지수를 완전제곱 꼴로 만들고 나면 가우스 적분을 바로 이용할 수 있으므로 \begin{equation} \int \exp\left[ -\frac{N}{2J^2}\left( J_{ij} - \frac{J^2}{N}\left( \frac{J_0}{J^2} + \beta X \right) \right)^2 \right] dJ_{ij} = \sqrt{\frac{2J^2\pi}{N}} = \left( \frac{1}{J}\sqrt{\frac{N}{2\pi}} \right)^{-1} \end{equation} 이며, 이것이 적분식 앞의 계수를 상쇄하게끔 되어 있다. 따라서 \begin{align} \therefore &\int dJ_{ij} \ P(J_{ij}) \exp\left[ \beta J_{ij} \sum_{\alpha = 1}^n S_{i}^{\alpha}S_{j}^{\alpha} \right] = \exp\left( \frac{\beta J_0}{N}X + \frac{\beta^2 J^2}{2N}X^2 \right) \\ &= \exp\left[ \frac{1}{N}\beta J_0 \left( \sum_{\alpha=1}^n S_{i}^{\alpha}S_{j}^{\alpha} \right) + \frac{1}{2N}\beta^2 J^2 \left( \sum_{\alpha=1}^n S_{i}^{\alpha}S_{j}^{\alpha} \right) \left( \sum_{\beta=1}^n S_{i}^{\beta}S_{j}^{\beta} \right) \right] \end{align} 이 되어 서로 다른 복제본들 사이의 결합항이 나타난다. 임시적인 결론으로서, $n$개의 복제본에 대한 분배함수의 무질서평균은 아래의 형태로 쓰여진다. \begin{align} \therefore \left[Z^n\right] = \text{Tr}_n \exp \left[ \frac{1}{N} \sum_{i<j} \left( \frac{1}{2}\beta^2 J^2 \sum_{\alpha\beta} S_{i}^{\alpha} S_{j}^{\alpha} S_{i}^{\beta} S_{j}^{\beta} + \beta J_0 \sum_\alpha S_{i}^{\alpha} S_{j}^{\alpha} \right) + \beta h \sum_{i} \sum_{\alpha} S_{i}^{\alpha} \right] \end{align}

위에 나타난 스핀들 사이의 결합항 $Y \equiv \sum_{i<j} \sum_{\alpha\beta} S_{i}^{\alpha} S_{j}^{\alpha} S_{i}^{\beta} S_{j}^{\beta}$와 $W \equiv \sum_{i<j} \sum_{\alpha} S_{i}^{\alpha} S_{j}^{\alpha}$를 조사해보자. 먼저 $Y$에서 인덱스들 간의 대소관계를 살펴보면 아래처럼 고쳐 쓸 수 있다: \begin{align} Y &= \sum_{i<j} \sum_{\alpha = 1}^{n} \sum_{\beta = 1}^{n} S_{i}^{\alpha} S_{j}^{\alpha} S_{i}^{\beta} S_{j}^{\beta} \\ &= \sum_{i<j} \left( \sum_{\alpha < \beta} S_{i}^{\alpha} S_{j}^{\alpha} S_{i}^{\beta} S_{j}^{\beta} + \sum_{\alpha = \beta} S_{i}^{\alpha} S_{j}^{\alpha} S_{i}^{\beta} S_{j}^{\beta} + \sum_{\alpha > \beta} S_{i}^{\alpha} S_{j}^{\alpha} S_{i}^{\beta} S_{j}^{\beta} \right) \\ &= \sum_{i<j} \left[ 2 \sum_{\alpha < \beta} S_{i}^{\alpha} S_{j}^{\alpha} S_{i}^{\beta} S_{j}^{\beta} + \sum_{\alpha} \left( S_{i}^{\alpha} S_{j}^{\alpha} \right)^2 \right] \\ &= \sum_{i<j} \left[ 2 \sum_{\alpha < \beta} S_{i}^{\alpha} S_{j}^{\alpha} S_{i}^{\beta} S_{j}^{\beta} + n \right] \\ &= \sum_{i,j} \left[ 2 \sum_{\alpha < \beta} S_{i}^{\alpha} S_{j}^{\alpha} S_{i}^{\beta} S_{j}^{\beta} + n \right] - \sum_{i>j} \left[ 2 \sum_{\alpha < \beta} S_{i}^{\alpha} S_{j}^{\alpha} S_{i}^{\beta} S_{j}^{\beta} + n \right] - \sum_{i=j} \left[ 2 \sum_{\alpha < \beta} S_{i}^{\alpha} S_{j}^{\alpha} S_{i}^{\beta} S_{j}^{\beta} + n \right]. \end{align} 여기에서 두 번째 항은 그 바로 윗줄의 $Y$ 표현식과 사실상 동일하다. 이를 좌변으로 넘겨 $2Y$라고 쓰도록 하자. 그리고 마지막 항은 $i=j$인 경우만 다루므로 $S_i^\alpha S_j^\alpha S_i^\beta S_j^\beta = 1$이다. 이를 $\alpha<\beta$에 대해 더하므로 답은 $n(n-1)/2$가 나온다. 이를 대입하자. \begin{equation} \therefore 2Y = \sum_{i,j} \left[ 2 \sum_{\alpha < \beta} S_{i}^{\alpha} S_{j}^{\alpha} S_{i}^{\beta} S_{j}^{\beta} + n \right] - \sum_i \left( n^2 - n + n \right) \end{equation} 이때 $\sum_{ij}$을 가진 앞의 항은 $N^2$에 비례하는 기여를 하고 $\sum_i$만을 가진 뒤의 항은 $N$에 비례하는 기여를 하는데, $N \gg 1$인 경우를 다루고 있으므로 뒤의 항은 무시할 수 있다. 그러므로 \begin{equation} Y \cong \sum_{i,j} \sum_{\alpha < \beta} S_{i}^{\alpha} S_{j}^{\alpha} S_{i}^{\beta} S_{j}^{\beta} + \frac{N^2}{2}n = \sum_{\alpha < \beta} \left( \sum_i S_{i}^{\alpha} S_{i}^{\beta} \right)^2 + \frac{N^2}{2}n \end{equation} 이다.

$W$에서도 인덱스 $i$와 $j$ 사이의 대소관계를 살펴보면 다음처럼 고쳐쓰게 된다: \begin{align} W &= \sum_{i<j} \sum_{\alpha} S_{i}^{\alpha} S_{j}^{\alpha} \\ &= \sum_{i,j} \sum_{\alpha} S_{i}^{\alpha} S_{j}^{\alpha} - \sum_{i>j} \sum_{\alpha} S_{i}^{\alpha} S_{j}^{\alpha} - \sum_{i=j} \sum_{\alpha} S_{i}^{\alpha} S_{j}^{\alpha}. \end{align} 이 때 $\sum_{i>j} \sum_{\alpha} S_{i}^{\alpha} S_{j}^{\alpha}$ 는 $i$와 $j$ 인덱스만 바꾸면 $W$와 같으므로 \begin{equation} 2W = \sum_{i,j} \sum_{\alpha} S_{i}^{\alpha} S_{j}^{\alpha} - \sum_i \sum_\alpha \left( S_{i}^{\alpha} \right)^2 \end{equation} 이며 $\left( S_i^\alpha \right)^2 = 1$임은 자명하다. 여기에서도 앞의 항은 $N^2$에 비례하고 뒤의 항은 $N$에 비례하므로 뒤의 항은 무시한다. \begin{equation} W = \frac{1}{2}\sum_{\alpha} \left( \sum_i S_{i}^{\alpha} \right)^2 - \frac{N}{2}n \cong \frac{1}{2} \sum_{\alpha} \left( \sum_i S_{i}^{\alpha} \right)^2 \end{equation}

따라서 $N \gg 1$ 이면, \begin{align} \left[ Z^n \right] &\cong \text{Tr}_n \exp \left\{ \frac{\beta^2 J^2}{2N} \left[ \sum_{\alpha < \beta} \left( \sum_i S_{i}^{\alpha} S_{i}^{\beta} \right)^2 + \frac{N^2}{2}n \right] + \frac{\beta J_0}{2N} \sum_{\alpha} \left( \sum_i S_{i}^{\alpha} \right)^2 + \beta h \sum_{i} \sum_{\alpha} S_{i}^{\alpha} \right\} \\ &= \exp\left( \frac{\beta^2 J^2}{4}Nn \right) \text{Tr}_n \exp \left\{ \frac{\beta^2 J^2}{2N} \sum_{\alpha < \beta} \left( \sum_i S_{i}^{\alpha} S_{i}^{\beta} \right)^2 + \frac{\beta J_0}{2N}\sum_{\alpha}\left(\sum_i S^{\alpha}_i\right)^2+ \beta h \sum_{i} \sum_{\alpha} S_{i}^{\alpha} \right\} \end{align} 이다.

여기서 제곱항을 처리해주기 위해 허바드-스트라토노비치 변환을 취하자 (해당 페이지에서 $a = \beta^2 J^2$과 $x = \frac{1}{\sqrt{N}}\sum_i S_i^{\alpha} S_i^{\beta}$를 대입해준 것과 같다). 이 과정에서 보조장(auxiliary field)인 $q_{\alpha \beta}$가 도입된다: \begin{equation} \exp \left[ \frac{\beta^2 J^2}{2N} \left( \sum_i S_{i}^{\alpha} S_{i}^{\beta} \right)^2 \right] = \sqrt{\frac{\beta^2 J^2 N}{2\pi}} \int_{-\infty}^{\infty} dq_{\alpha \beta} \ \exp \left[ -\frac{N \beta^2 J^2}{2} q_{\alpha \beta}^2 + \beta^2 J^2 q_{\alpha \beta} \left( \sum_i S_{i}^{\alpha} S_{i}^{\alpha} \right) \right]. \end{equation} 또다른 제곱항은 보조장 $m_{\alpha}$를 도입하여 마찬가지로 허바드-스트라토노비치 변환을 취한다: \begin{equation} \exp \left[ \frac{\beta J_0}{2N} \left(\sum_i S_i^{\alpha} \right)^2 \right] = \sqrt{\frac{\beta J_0 N}{2 \pi}} \int_{-\infty}^{\infty} dm_{\alpha} \ \exp \left[ -\frac{N \beta J_0}{2}m_{\alpha}^2 + \beta J_0 m_{\alpha} \left( \sum_i S_{i}^{\beta} \right) \right]. \end{equation} 이 표현식들을 대입하고, 변환으로 인해 생기는 계수들을 생략한다면 다음처럼 적을 수 있다: \begin{equation} \left[ Z^n \right] ~\propto~ \exp \left( \frac{\beta^2 J^2}{4}Nn \right) \int \prod_{\alpha < \beta} dq_{\alpha \beta} \int \prod_{\alpha} dm_{\alpha} \exp \left( -\frac{N \beta^2 J^2}{2} \sum_{\alpha < \beta} q_{\alpha \beta}^2 - \frac{N \beta J_0}{2}\sum_{\alpha} m_{\alpha}^2 \right) \text{Tr}_n \exp \left( \beta^2 J^2 \sum_{\alpha < \beta} q_{\alpha \beta} \sum_i S_{i}^{\alpha} S_{i}^{\beta} + \beta \sum_{\alpha} \left( J_0 m_{\alpha} + h \right) \sum_i S_{i}^{\alpha} \right). \end{equation} 끄트머리의 지수 함수 안에 스핀 위치에 대한 합 $\sum_i$만이 들어있음에 주의하자. 일반적으로 \begin{equation} \text{Tr}_n \exp\left( \sum_i^N L_i \right) = \left( \text{Tr}^\prime e^L \right)^N \end{equation} 과 같은 식으로 분해해서 쓸 수 있다. 예를 들어 $N=2$이고 $n=1$이라면 \begin{align} \text{Tr}_n \exp \left( L_1 + L_2 \right) &= e^{L_1^{+}}e^{L_2^{+}} + e^{L_1^{+}}e^{L_2^{-}} + e^{L_1^{-}}e^{L_2^{+}} + e^{L_1^{-}}e^{L_2^{-}} \\ &= \left( e^{L_1^{+}} + e^{L_1^{-}} \right) \left( e^{L_2^{+}} + e^{L_2^{-}} \right) \end{align} 이라는 뜻이다. 혹은 $N=2$이고 $n=2$라면 \begin{align} \text{Tr}_n \exp \left( L_1 + L_2 \right) &= \left( e^{L_1^{++}} + e^{L_1^{+-}} + e^{L_1^{-+}} + e^{L_1^{--}} \right) \left( e^{L_2^{++}} + e^{L_2^{+-}} + e^{L_2^{-+}} + e^{L_2^{--}} \right) \end{align} 처럼 될 것이다. 물론 $\left( \text{Tr}^\prime e^L \right)^N = \exp \left( N\ln \text{Tr}^{\prime} e^{L} \right)$로도 쓸 수 있다. 여기서 $\text{Tr}^{\prime}$은 특정 위치의 스핀 하나에 대해 취하는 대각합이다 (단, 위치 $i$만을 고정했을 뿐, 다른 복제본들이 개입되었을 수는 있음). 지금의 경우 \begin{align} L \equiv \beta^2 J^2 \sum_{\alpha < \beta} q_{\alpha \beta} S^{\alpha} S^{\beta} + \beta \sum_{\alpha} \left( J_0 m_{\alpha} + h \right) S^{\alpha} \end{align} 가 된다. 다시 정리하면, 분배함수의 무질서평균은 아래와 같다: \begin{equation} \left[ Z^n \right] ~=~ \exp \left( \frac{N \beta^2 J^2 n}{4} \right) \int \prod_{\alpha < \beta} dq_{\alpha \beta} \int \prod_{\alpha} dm_{\alpha} \exp \left( -\frac{N \beta^2 J^2}{2} \sum_{\alpha < \beta} q_{\alpha \beta}^2 - \frac{N \beta J_0}{2}\sum_{\alpha} m_{\alpha}^2 \right) \exp \left( N\ln \text{Tr}^{\prime} e^{L} \right). \end{equation}

안장점 근사를 사용하면 $N \to \infty$에서는 적분되고 있는 지수함수 안의 표현식 \begin{equation} -\frac{\beta^2 J^2}{2} \sum_{\alpha < \beta} q_{\alpha \beta}^2 - \frac{\beta J_0}{2}\sum_{\alpha} m_{\alpha}^2 + \ln \text{Tr}^{\prime} e^{L} \end{equation} 가 최대가 되는 지점이 적분의 값을 결정할 것이라고 논할 수 있다. 이는 위 표현식을 $q_{\alpha \beta}$와 $m_\alpha$로 편미분한 값이 모두 0이 되게끔 하면 찾을 수 있으며, 그 결과는 아래와 같다. \begin{align} &q_{\alpha \beta} = \frac{1}{\beta^2 J^2} \frac{\partial}{\partial q_{\alpha \beta}} \ln \text{Tr}^{\prime} e^{L} = \frac{\text{Tr}^{\prime} S^{\alpha} S^{\beta} e^{L}}{\text{Tr}^{\prime} e^{L}} \\ &m_{\alpha} = \frac{1}{\beta J_0} \frac{\partial}{\partial m_{\alpha}} \ln \text{Tr}^{\prime} e^{L} = \frac{\text{Tr}^{\prime} S^{\alpha} e^{L}}{\text{Tr}^{\prime} e^{L}} \end{align} 안장점 근사를 사용해 적분을 수행한 결과는 위에서 찾아진 $q_{\alpha \beta}$와 $m_\alpha$를 피적분함수에 대입해 적분 밖으로 끄집어낸 결과와 비례한다. 적분으로 인해 얻어지는 비례상수들을 모두 모아서 $C^n$으로 적어놓으면 아래와 같이 쓸 수 있다: \begin{align} \left[ Z^n \right] \propto C^n \exp \left[ -\frac{N \beta^2 J^2}{2} \sum_{\alpha < \beta} q_{\alpha \beta}^2 - \frac{N \beta J_0}{2} \sum_{\alpha} m_{\alpha}^2 + N\ln \text{Tr}^{\prime} e^{L} + \frac{N}{4}\beta^2 J^2 n \right]. \end{align}

이제 입자 하나당의 (무질서평균이 이루어진) 자유에너지 $\left[ f \right]$는 다음의 식을 만족한다. \begin{align} -\beta [f] =& \lim_{n \rightarrow 0} \frac{\left[ Z^n \right] - 1}{nN} = \lim_{n \rightarrow 0} \frac{1}{nN} \left[ -\frac{N \beta^2 J^2}{4} \sum_{\alpha \neq \beta} q_{\alpha \beta}^2 - \frac{N \beta J_0}{2} \sum_{\alpha} m_{\alpha}^2 + \frac{Nn}{4}\beta^2 J^2 + N\ln \text{Tr}^{\prime} e^{L} \right] \\ =& \lim_{n \rightarrow 0} \left[ -\frac{\beta^2 J^2}{4n} \sum_{\alpha \neq \beta} q_{\alpha \beta}^2 - \frac{\beta J_0}{2n} \sum_{\alpha} m_{\alpha}^2 + \frac{\beta^2 J^2}{4} + \frac{1}{n}\ln \text{Tr}^{\prime} e^{L} \right] \end{align}

한 위치에서 복제본 사이의 상관관계를 보기 위해 $S_{i}^{\alpha} S_{i}^{\beta}$의 기대값을 계산하자. 먼저 열적평균(thermal average, $\left< \ldots \right>$)을 취한 다음 무질서평균을 취한다. \begin{align} \left[ \big\langle S_{i}^{\alpha} S_{i}^{\beta} \big\rangle \right] =& \left[ \frac{\text{Tr}_n \ S_{i}^{\alpha} S_{i}^{\beta} \exp \left( -\beta \sum_{\gamma} H^{\gamma} \right)}{\text{Tr}_n \ \exp \left( -\beta\sum_{\gamma} H^{\gamma} \right) } \right] \end{align} 여기에서 $H^\gamma = -\sum_{i<j} J_{ij} S_i^\gamma S_j^\gamma - h\sum_i S_i^\gamma$이다. 분모에서 $\text{Tr}_n \ \exp \left( -\beta\sum_{\gamma} H^{\gamma} \right) = Z^n$이고 $n\to 0$에서 이는 $1$로 수렴할 것이므로 우리가 고려해야 할 것은 다음과 같은 양이다: \begin{align} &\left[ \text{Tr}_n \ S_{i}^{\gamma} S_{i}^{\delta} \exp \left( -\beta \sum_{\alpha} H^{\alpha} \right) \right]\\ &= \int \left[ \prod_{i < j} dJ_{ij} \ P(J_{ij}) \right] \text{Tr}_n S_{k}^{\gamma} S_{k}^{\delta} \exp \left[ \beta \sum_{i < j} J_{ij} \sum_{\alpha = 1}^n S_{i}^{\alpha} S_{j}^{\alpha} + \beta h \sum_{i=1}^N \sum_{\alpha=1}^n S_{i}^{\alpha} \right] \\ &= C^{\prime} \exp \left( \frac{N \beta^2 J^2 n}{4} \right) \int \prod_{\alpha < \beta} dq_{\alpha \beta} \int \prod_{\alpha} dm_{\alpha} \ \exp \left( -\frac{N \beta ^2 J^2}{2} \sum_{\alpha < \beta} q_{\alpha \beta}^2 - \frac{N \beta J_0}{2} \sum_{\alpha} m_{\alpha}^2 \right) \text{Tr}_n S_{k}^{\gamma} S_{k}^{\delta} \exp \left[ \beta^2 J^2 \sum_{\alpha < \beta} q_{\alpha \beta} \sum_i S_{i}^{\alpha} S_{i}^{\beta} + \beta \sum_{\alpha} \left( J_0 m_{\alpha} + h \right) \sum_{i} S_{i}^{\alpha} \right]. \end{align} 여기서 $\text{Tr}_n$ 부분을 계산할 때, $i\neq k$이면 앞과 똑같이 $\text{Tr}^{\prime} e^L$만큼을 내어놓고 $i=k$일 때에만 $\text{Tr}^{\prime} \left( S_{k}^{\gamma} S_{k}^{\delta} e^L \right)$을 주므로 \begin{align} \therefore \left[ \big\langle S_{i}^{\alpha} S_{i}^{\beta} \big\rangle \right] =& \left[ \text{Tr} \ S_{i}^{\alpha} S_{i}^{\beta} \exp \left( -\beta \sum_{\gamma} H^{\gamma} \right) \right] \\ =& \left( \text{Tr}^{\prime} e^L \right)^{N-1} \text{Tr}^{\prime} \left( S_{i}^{\alpha} S_{i}^{\beta} e^L \right). \end{align} 모든 스핀은 평균적으로 동등하므로 $i$라는 인덱스는 떼어버려도 되겠다. $n \rightarrow 0$인 극한에서 $\text{Tr}^{\prime} e^L \to 1$ 이므로 위 식은 $q_{\alpha \beta} = \text{Tr}^\prime S^\alpha S^\beta e^L / \text{Tr}^\prime e^L$과 같아진다. 즉, \begin{equation} q_{\alpha \beta}=\left[ \big\langle S_{i}^{\alpha} S_{i}^{\beta} \big\rangle \right]. \end{equation} 마찬가지 논법으로, \begin{equation} m_{\alpha}=\left[ \big\langle S_{i}^{\alpha} \big\rangle \right] \end{equation} 이다.

이것으로 볼 때 $m$은 일반적으로 사용되는 강자성 질서맺음변수(ferromagnetic order parameter)로 해석할 수 있으며, $q_{\alpha \beta}$는 스핀유리 질서맺음변수(spin glass order parameter)라고 불린다. 복제본들은 서로 독립적이므로 상관함수는 쪼개어 쓸 수 있고, 그래서 만일 복제본들이 대칭성(replica symmetry)을 가진다면 \begin{equation} q_{\alpha \beta} = \left[ \left< S_i^\alpha S_i^\beta \right> \right] = \left[ \left< S_i^\alpha \right> \left< S_i^\beta \right> \right] = \left[ \left< S_i \right>^2 \right] = q \end{equation} 와 같은 형태가 된다. 스핀유리상(spin glass phase)에서 스핀들은 위아래를 가리킨 채로 굳어있게(frozen) 될 텐데 따라서 개별 스핀은 $\left< S_i \right> \neq 0$일 것이다. 무질서에 대해 평균을 내면 $m=\left[ \big\langle S_{i} \big\rangle \right]=0$이 될 테지만, $q = \left[ \left< S_i \right>^2 \right]$은 양수인 값을 가지는 것이 가능하다.

상자성 상(paramagnetic phase)에서는 $m=q=0$이고, 강자성 상(ferromagnetic phase)에서는 $m$과 $q$ 모두 0이 아닌 값을 가진다.

방금 본 것처럼 복제 대칭성이 있으면 $q_{\alpha\beta} = q$와 $m_{\alpha} = m$로 쓸 수 있다. 헬름홀츠 자유에너지는 \begin{align} -\beta [f] =& -\frac{\beta^2 J^2}{4n} \sum_{\alpha \neq \beta} q_{\alpha \beta}^2 - \frac{\beta J_0}{2n} \sum_{\alpha} m_{\alpha}^2 + \frac{\beta^2 J^2}{4} + \frac{1}{n} \ln \text{Tr}^{\prime} e^L \\ =& -\frac{\beta^2 J^2}{4} \left( n-1 \right) q^2 - \frac{\beta J_0}{2} m^2 + \frac{1}{n} \ln \text{Tr}^{\prime} e^L + \frac{\beta^2 J^2}{4} \end{align} 인데, 대각합 부분을 다음처럼 계산해보자. \begin{align} \text{Tr}^{\prime} e^L =& \text{Tr}^{\prime} \exp \left[ \beta^2 J^2 \sum_{\alpha < \beta} q_{\alpha\beta} S^{\alpha} S^{\beta} + \beta \sum_{\alpha} \left( J_0 m_{\alpha} + h \right) S^{\alpha} \right] \\ =& \text{Tr}^{\prime} \exp \left[ \beta^2 J^2 q \sum_{\alpha < \beta} S^{\alpha} S^{\beta} + \beta \left( J_0 m_{\alpha} + h \right) \sum_{\alpha} S^{\alpha} \right] \\ =& \text{Tr}^{\prime} \exp \left\{ \beta^2 J^2 q \frac{1}{2} \left[ \left( \sum_{i} S_{i}^{\alpha} \right)^2 - n \right] + \beta \left( J_0 m_{\alpha} + h \right) \sum_{\alpha} S^{\alpha} \right\} \\ =& \text{Tr}^{\prime} \sqrt{\frac{\beta^2 J^2 q}{2\pi}} \int_{-\infty}^{\infty} dz \ \exp\left[ -\beta^2 J^2 q \frac{z^2}{2} + \beta^2 J^2 q z \sum_{\alpha} S^{\alpha} - \frac{n}{2} \beta^2 J^2 q + \beta \left( J_0 m + h \right) \sum_{\alpha} S^{\alpha} \right] \end{align} 마지막 줄에서는 $a = \beta^2 J^2 q$, $z = \sqrt{N}m$, 그리고 $x = \sum_{\alpha} S^{\alpha}$인 허바드-스트라토노비치 변환을 사용했다. 대각합은 스핀 변수에 걸리는 것이므로 적분식 안쪽으로 밀어넣고 $\tilde{z} \equiv \beta J \sqrt{q} z$로 정의하자. \begin{align} \text{Tr}^{\prime} e^L =& \sqrt{\frac{\beta^2 J^2 q}{2\pi}} \int_{-\infty}^{\infty} dz \ \exp\left( -\beta^2 J^2 q \frac{z^2}{2} \right) \text{Tr}^{\prime} \exp \left\{ \left[ \beta^2 J^2 q z + \beta \left( J_0 m + h \right) \right] \sum_{\alpha} S^{\alpha} \right\} \exp \left( -\frac{n}{2}\beta^2 J^2 q \right) \\ =& \frac{1}{\sqrt{2\pi}} \int_{-\infty}^{\infty} d\tilde{z} \exp\left( -\frac{\tilde{z}^2}{2} \right) \text{Tr}^{\prime} \exp \left\{ \left[ \beta J \sqrt{q} \tilde{z} + \beta \left( J_0 m + h \right) \right] \sum_{\alpha} S^{\alpha} \right\} \exp \left( -\frac{n}{2}\beta^2 J^2 q \right) \\ =& \int D\tilde{z} \ \left[ 2\cosh \left( \beta J \sqrt{q} \tilde{z} + \beta J_0 m + \beta h \right) \right]^n \exp \left( -\frac{n}{2}\beta^2 J^2 q \right) \end{align} 이 과정에서 \begin{align} \frac{1}{\sqrt{2\pi}} \int_{-\infty}^{\infty} d\tilde{z} \exp\left( -\frac{\tilde{z}^2}{2} \right) \ldots \equiv \int D\tilde{z} \ldots \end{align} 으로 줄여서 적었다 (참고로 $\int D\tilde{z} = 1$). 그리고 $\cosh$ 내부도 간단히 적기 위해 $\tilde{H} (\tilde{z}) \equiv J \sqrt{q} \tilde{z} + J_0 m + h$을 도입한 다음 양변에 자연로그를 취하면, \begin{align} \ln \text{Tr}^{\prime} e^L =& \ln \int D\tilde{z} \exp \left\{ n \ln \left[ 2\cosh \beta \tilde{H} \left( \tilde{z} \right) \right] - \frac{n}{2} \beta^2 J^2 q \right\} \\ \approx& \ln \int D\tilde{z} \left\{ 1+ n \ln \left[ 2\cosh \beta \tilde{H} \left( \tilde{z} \right) \right] - \frac{n}{2} \beta^2 J^2 q \right\} \\ \approx& \ln \left\{ 1+ n \int D\tilde{z} \ln \left[ 2\cosh \beta \tilde{H} \left( \tilde{z} \right) \right] - \frac{n}{2} \beta^2 J^2 q \right\}\\ \underset{n \rightarrow 0}{\longrightarrow}& \ n \left\{ \int D\tilde{z} \ln \left[ 2\cosh \beta \tilde{H} \left(\tilde{z}\right) \right] - \frac{1}{2}\beta^2 J^2 q \right\}. \end{align} 그러므로 \begin{align} \lim_{n \rightarrow 0} \left( -\beta \left[ f \right] \right) =& \frac{\beta^2 J^2}{4}q^2 - \frac{\beta J_0}{2}m^2 + \int D\tilde{z} \ln \left[ 2\cosh \beta \tilde{H} \left(\tilde{z}\right) \right] - \frac{1}{2}\beta^2 J^2 q + \frac{\beta^2 J^2}{4} \\ =& \frac{\beta^2 J^2}{4} \left( q^2 - 2q + 1 \right) - \frac{1}{2} \beta J_0 m^2 + \int D\tilde{z} \ln \left[ 2\cosh \beta \tilde{H} \left(\tilde{z}\right) \right] \\ =& \frac{\beta^2 J^2}{4} \left( 1 - q \right)^2 - \frac{\beta J_0}{2}m^2 + \int D\tilde{z} \ln \left[ 2\cosh \beta \tilde{H} \left(\tilde{z}\right) \right] \end{align} 이다.

자유에너지 범함수를 최소로 하기 위해 미분을 취하면 자기일관성(self-consistency)을 위한 방정식을 얻게 된다. 먼저 $m$에 대해: \begin{equation} 0 = \frac{\partial}{\partial m} \left\{ -\lim_{n \rightarrow 0} \beta \left[ f \right] \right\} = -\beta J_0 m + \frac{\partial}{\partial m} \int D\tilde{z} \ln \left[ 2\cosh\beta\tilde{H}\left(\tilde{z}\right) \right] = -\beta J_0 m + \beta J_0 \int D\tilde{z} \tanh \beta \tilde{H} \left( \tilde{z} \right) \end{equation} \begin{equation} \therefore m = \int D\tilde{z} \tanh \beta \tilde{H}\left(\tilde{z}\right). \end{equation} 다음으로 $q$에 대해: \begin{align} 0 =& \frac{\partial}{\partial q} \left\{ -\lim_{n \rightarrow 0} \beta \left[ f \right] \right\} = \frac{\beta^2 J^2}{2}\left(q-1\right) + \beta J \int D\tilde{z} \tanh \beta \tilde{H}\left(\tilde{z}\right) \frac{\tilde{z}}{2\sqrt{q}} \\ =& \frac{\beta^2 J^2}{2}\left(q-1\right) + \frac{\beta J}{2\sqrt{q}} \int D\tilde{z} \ \tilde{z} \tanh \beta\tilde{H}\left(\tilde{z}\right) \end{align} 그런데 여기에서 마지막의 항을 부분적분하면 더 간단히 적을 수 있다: \begin{align} \int D\tilde{z} \ \tilde{z} \tanh \beta\tilde{H}\left(\tilde{z}\right) =& \frac{1}{\sqrt{2\pi}} \int d\tilde{z} \exp \left( -\frac{\tilde{z}^2}{2} \right) \tilde{z} \tanh \left(\beta J \sqrt{q} \tilde{z}\right) \\ =& - \frac{1}{\sqrt{2\pi}} \left[ \exp \left( -\frac{\tilde{z}^2}{2} \right) \tanh \left( \beta J \sqrt{q} \tilde{z} \right) \right]_{-\infty}^{\infty} + \frac{1}{\sqrt{2\pi}} \int d\tilde{z} \exp \left( -\frac{\tilde{z}^2}{2} \right) \beta J \sqrt{q} \ \text{sech}^2 \left( \beta J \sqrt{q} \tilde{z} \right) \\ =& \int D\tilde{z} \ \beta J \sqrt{q} \ \text{sech}^2 \left( \beta J \sqrt{q} \tilde{z} \right) \end{align} 이를 위의 식에 대입하면 \begin{equation} \frac{\beta^2 J^2}{2} \left(q-1\right) + \frac{\beta^2 J^2}{2} \int D\tilde{z} \ \text{sech}^2 \tilde{H} \left( \tilde{z} \right)=0 \end{equation} 이고 이 식을 정리하면 \begin{equation} q = 1 - \int D\tilde{z} \ \text{sech}^2 \tilde{H} \left( \tilde{z} \right) = \int D \tilde{z} \tanh^2 \beta \tilde{H} \left( \tilde{z} \right). \end{equation}

외부 자기장이 $h=0$이고 $J_{ij}$의 평균이 $J_0=0$인 상황을 고려하자. 그러면 \begin{equation} \tilde{H} \left( \tilde{z} \right) = J \sqrt{q} \tilde{z} \end{equation} 이 홀함수이기 때문에 $m = \int D\tilde{z} \ \tanh \beta J \sqrt{q} \tilde{z} = 0$이다. 이 결과를 자유에너지에 다시 대입하고 $\cosh$와 $\ln$을 급수전개하면: \begin{align} -\beta \left[ f \right] =& \frac{1}{4} \beta^2 J^2 \left( 1-q \right)^2 + \int D\tilde{z} \ \ln\left[ 2\cosh \left( \beta J \sqrt{q} \tilde{z} \right) \right] \\ \approx& \frac{1}{4} \beta^2 J^2 \left( 1-q \right)^2 + \ln 2 + \int D\tilde{z} \ln \left[ 1 + \frac{1}{2}\beta^2 J^2 q \tilde{z}^2 + \frac{1}{24}\beta^4 J^4 q^2 \tilde{z}^4 \right] \qquad \left( q \ll 1 \right) \\ \approx& \frac{1}{4} \beta^2 J^2 \left( 1-q \right)^2 + \ln 2 + \int D\tilde{z} \left( \frac{1}{2}\beta^2 J^2 q \tilde{z}^2 + \frac{1}{24}\beta^4 J^4 q^2 \tilde{z}^4 - \frac{1}{8}\beta^4 J^4 q^2 \tilde{z}^4 \right) \\ =& \frac{1}{4} \beta^2 J^2 + \ln 2 + \frac{1}{2}\beta^2 J^2 q - \frac{1}{4} \beta^4 J^4 q^2 \\ =& \frac{1}{4} \beta^2 J^2 + \ln 2 + \frac{1}{4}\beta^2 J^2 \left( 1 - \beta^2 J^2 \right)q^2. \end{align} 따라서 \begin{equation} \beta\left[ f \right] \cong -\frac{1}{4} \beta^2 J^2 - \ln 2 -\frac{1}{4}\beta^2 J^2 \left( 1 - \beta^2 J^2 \right)q^2 \end{equation} 이므로, 스핀유리 상전이는 $T = T_f \equiv J/k_B$에서 일어난다. 문제는 온도 $T$가 $T_f$보다 높아질 때 $q^2$ 앞의 계수가 음수가 되므로 마치 온도가 높아질 때에 스핀유리 상이 나타나는 듯이 보인다는 점이다. 이는 $n\to 0$을 취하는 이 방법의 문제점으로, 위에서 '자유에너지 범함수'의 부분을 보면 $n<1$일 때 $q^2$ 앞의 계수가 부호를 바꾸는 것을 볼 수 있다.

이제 $J_0 > 0$이면 $m$이 0이 아닌 값을 취할 수 있게 된다. 위에 적었던 방정식을 전개해서 $q$와 $m$의 가장 낮은 차수 항만을 남기면 $\tanh^2 x \approx x^2$이므로 \begin{align} q =& \int D\tilde{z} \ \tanh^2 \left( \beta J \sqrt{q} \tilde{z} + \beta J_0 m \right) \\ \approx& \int D\tilde{z} \left( \beta^2 J^2 q \tilde{z}^2 + 2\beta^2 J J_0 \sqrt{q} m\tilde{z} + \beta^2 J_0^2 m^2 \right) \\ =& \beta^2 J_0^2 m^2 + \beta^2 J^2 q. \end{align} 위의 식은 만일 $0<m \ll 1$이라면 $q \sim \mathcal{O}(m^2)$일 것임을 의미한다. 이제 $m$에 대한 방정식을 보면, \begin{align} m =& \int D\tilde{z} \ \tanh \left( \beta J \sqrt{q} \tilde{z} + \beta J_0 m \right) \\ \approx& \int D\tilde{z} \left( \beta J \sqrt{q} \tilde{z} + \beta J_0 m \right) \end{align} 인데 $\sqrt{q} \sim \mathcal{O}(m)$에 비례하는 부분은 적분에 의해 사라지고 적분 밖으로 빠져나오는 $q$ 의존성은 $\mathcal{O}(m)$에 비해 작을 것이다. 따라서 $m \approx \beta J_0 m$에서 상전이가 일어난다고 보아도 되며 이는 강자성 임계점이 $T_c = J_0/k_B$임을 뜻한다.

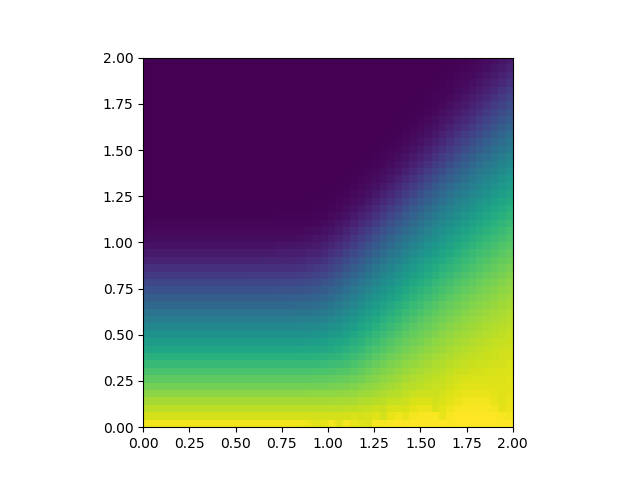
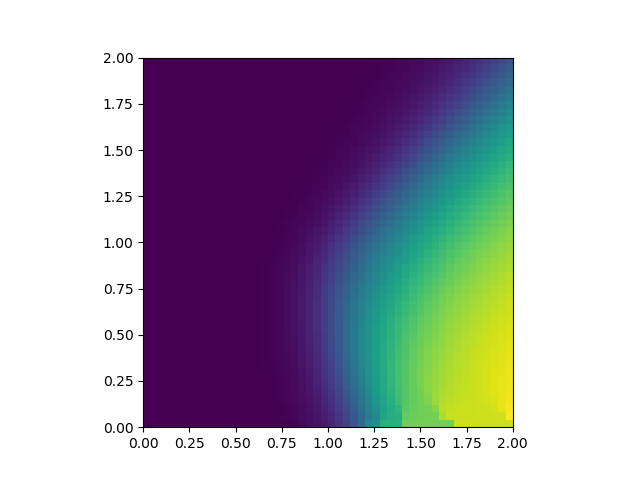
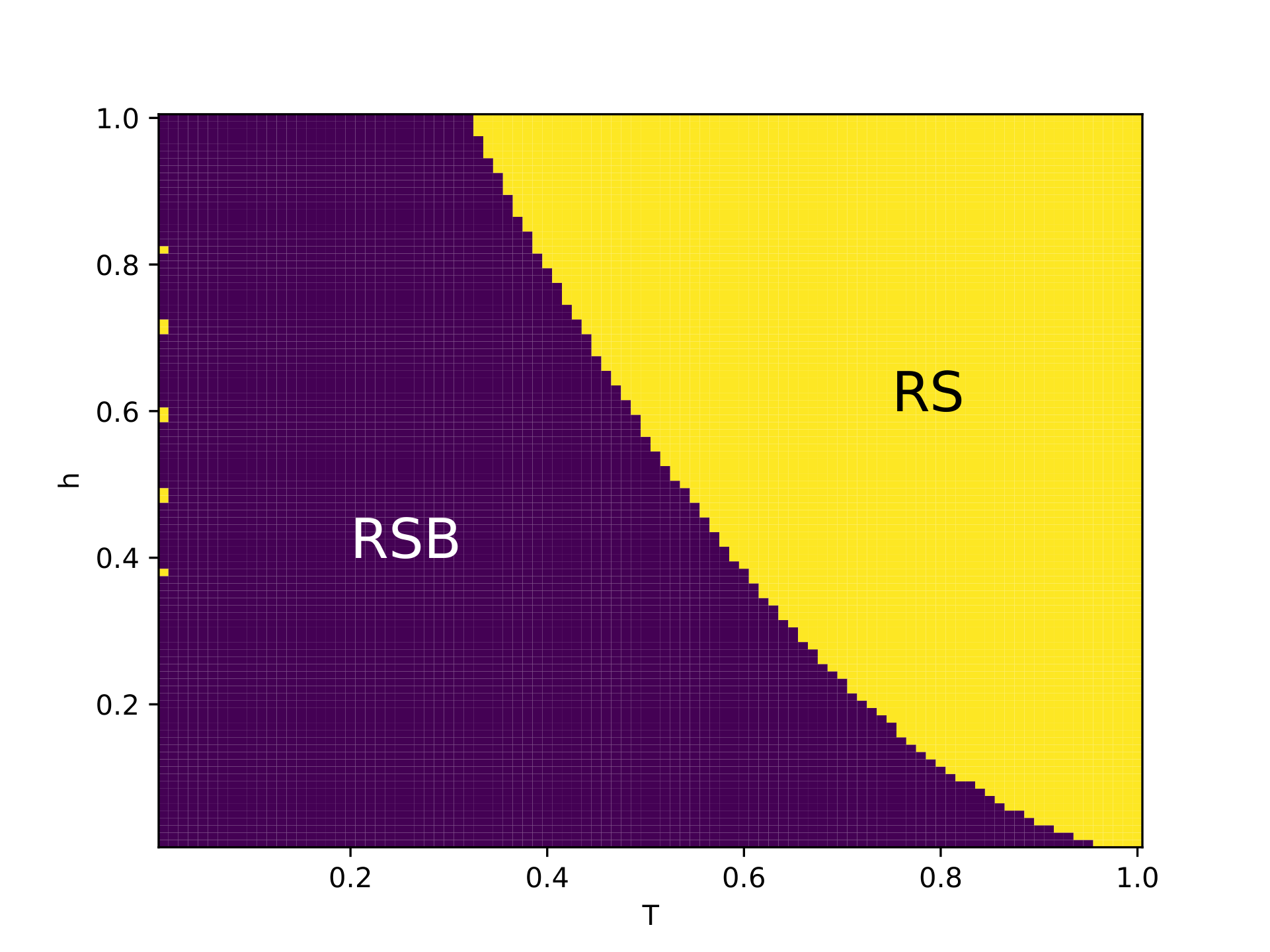
스핀유리와 강자성 사이의 경계는 앞의 식들을 수치적으로 풂으로써 찾을 수 있다. 아래 두 그림에서 가로축은 $J_0/J$, 세로축은 $k_B T/J$를 나타낸다. 첫 번째 그림은 $q$, 두 번째 그림은 $m$의 값을 나타내며, 밝을수록 1에 가깝다. 스핀유리상은 왼쪽 아래($q>0$, $m=0$)이며 강자성상은 오른쪽 아래($q>0$, $m>0$), 상자성상은 윗부분($q=m=0$)이다. 스핀유리상이 $J_0>J$인 영역까지도 조금 침범하고 있음을 볼 수 있다. 그러나 사실 이 영역은 복제대칭성 깨짐을 도입하면 사라진다.

$T \rightarrow 0$에서 $q = 1 - aT$처럼 쓸 수 있다고 가정하자. \begin{align} q =& 1 - \int D\tilde{z} \ \text{sech}^2 \beta J \sqrt{q} \tilde{z} \approx 1 - \int D\tilde{z} \ \text{sech}^2 \beta J \tilde{z} = 1 - \frac{1}{\beta J} \int D\tilde{z} \ \frac{d}{d\tilde{z}} \tanh \beta J \tilde{z} \\ \underset{\beta \rightarrow \infty}{\longrightarrow} & 1 - \frac{1}{\beta J} \int D\tilde{z} \ 2\delta\left( \tilde{z} \right) = 1 - \frac{1}{\beta J} \frac{1}{\sqrt{2\pi}} 2 = 1 - \sqrt{\frac{2}{\pi}} \cdot \frac{k_B}{J} \cdot T \end{align} 이므로 앞의 가정과 일치하려면 $a = k_B\sqrt{2/\pi}/J$임을 알 수 있다.

$J_0 = 0$인 경우 자유에너지 표현식에 위 결과를 대입해보자: \begin{align} -\beta \left[ f \right] =& \frac{1}{4} \beta^2 J^2 \left( 1-q \right)^2 + \int D\tilde{z} \ \ln\left[ 2\cosh \left( \beta J \sqrt{q} \tilde{z} \right) \right] \\ \approx& \frac{1}{4}\beta^2 J^2 \frac{2}{\pi} \frac{1}{\beta^2 J^2} + 2 \int_0^{\infty} D\tilde{z} \ \ln\left[ \exp\left( \beta J \sqrt{q} \tilde{z} \right) + \exp\left( - \beta J \sqrt{q} \tilde{z} \right) \right] \\ =& \frac{1}{2\pi} + 2\int_0^{\infty} D\tilde{z} \ \ln \left\{ \exp \left( \beta J \sqrt{q} \tilde{z} \right) \left[ 1 + \exp \left( -2\beta J \sqrt{q} \tilde{z} \right) \right] \right\} \\ =& \frac{1}{2\pi} + 2\int_0^{\infty} D\tilde{z} \ \left[ \beta J \sqrt{q} \tilde{z} + \ln \left( 1 + e^{-2\beta J \sqrt{q} \tilde{z}} \right) \right] \\ \approx& \frac{1}{2\pi} + \sqrt{\frac{2}{\pi}}\beta J \sqrt{q} + 2 \int_0^{\infty} D\tilde{z} \ e^{-2\beta J \sqrt{q} \tilde{z}} \end{align} 뒤의 적분항은 $\beta \gg 1$ 인 경우 무시할 수 있으므로 \begin{align} \therefore \ -\beta \left[ f \right] \approx& \frac{1}{2\pi} + \sqrt{\frac{2}{\pi}}\beta J \left( 1 - \frac{1}{2}\sqrt{\frac{2}{\pi}}\frac{1}{\beta J} \right) \\ =& \frac{1}{2\pi} + \sqrt{\frac{2}{\pi}}\beta J - \frac{1}{2} \cdot \frac{2}{\pi} = -\frac{1}{2\pi} + \sqrt{\frac{2}{\pi}}\beta J \end{align} 양변에 $\beta$를 곱하면 \begin{equation} \left[ f \right] \approx \frac{k_B T}{2\pi} - \sqrt{\frac{2}{\pi}}J \end{equation} 인데, 이를 $E-TS$라는 자유에너지 표현식과 비교하면 바닥상태의 에너지가 $-\sqrt{2/\pi}J$이며 그때 엔트로피가 $-k_B/(2\pi)$임을 유추할 수 있다. 엔트로피가 음수라고 하는 이 이상한 거동은 파리시(G. Parisi)가 복제 대칭성 깨짐(replica symmetry breaking)을 도입함으로써 해결했다.

위에서 $n$개의 복제본에 대한 자유에너지를 다음처럼 적었다: $$ -\beta[f] = \lim_{n\rightarrow0}\left\{-\frac{\beta^2J^2}{4n}\sum_{\alpha\neq\beta}q_{\alpha\beta}^2 - \frac{\beta J_0}{2n}\sum_\alpha m_\alpha^2 + \frac14\beta^2J^2+\frac1n\ln\text{Tr}' e^L \right\}. $$

여기서 $h=0$으로 놓고 $\beta Jq_{\alpha\beta} \equiv y^{\alpha\beta}$와 $\sqrt{\beta J_0}m_\alpha \equiv x^\alpha$을 정의하면 자유에너지는

$$ [f] = -\frac{\beta J^2}{4} - \lim_{n\rightarrow0}\frac{1}{\beta n}\left\{-\sum_{\alpha\beta}\frac12(y^{\alpha\beta})^2 - \sum_\alpha\frac12(x^\alpha)^2 + \ln\text{Tr}' \exp \left(\beta J\sum_{\alpha<\beta}y^{\alpha\beta}S^\alpha S^\beta + \sqrt{\beta J_0} \sum_\alpha x^\alpha S^\alpha\right) \right\} $$

가 된다. 복제 대칭해가 안정적인지를 보려면 질서 변수들이 복제 대칭해를 조금 벗어나도록 하고 이들의 계수의 부호를 보면 될 것이다. 즉 $$ x^\alpha = x+\epsilon^\alpha,\quad y^{\alpha\beta} = y + \eta^{\alpha\beta} $$ 로 두고 $\eta^{\alpha\beta}$, $\epsilon^\alpha$로 전개할 것이다. 먼저 $\ln\text{Tr}' \exp$항은 $$ \ln\text{Tr}' \exp\left(L_0+\beta J\sum_{\alpha<\beta}\eta^{\alpha\beta}S^\alpha S^\beta + \sqrt{\beta J_0}\sum_\alpha \epsilon^\alpha S^\alpha\right) $$

인데, 여기서 $L_0 = \beta Jy\sum_{\alpha<\beta}S^\alpha S^\beta + \sqrt{\beta J_0}x\sum_\alpha S^\alpha$로, $\epsilon^\alpha$ 및 $\eta^{\alpha\beta}$와는 상관없는 항이다. 그러므로 $L_0$를 빼고 $\exp$항을 2차항까지 전개하면 ($e^x = 1+x+x^2/2 + \ldots$)

\begin{align*} &\ln\text{Tr}' \exp\left(L_0+\beta J\sum_{\alpha<\beta}\eta^{\alpha\beta}S^\alpha S^\beta + \sqrt{\beta J_0}\sum_\alpha\epsilon^\alpha S^\alpha\right)\\ =&\ln\text{Tr}'e^{L_0}\left[1+\beta J\sum_{\alpha<\beta}\eta^{\alpha\beta}S^\alpha S^\beta + \sqrt{\beta J_0}\sum_\alpha\epsilon^\alpha S^\alpha+\frac12\left(\beta J\sum_{\alpha<\beta}\eta^{\alpha\beta}S^\alpha S^\beta + \sqrt{\beta J_0}\sum_\alpha\epsilon^\alpha S^\alpha\right)^2\right]\\ =&\ln\left[\text{Tr}'e^{L_0}+\text{Tr}'e^{L_0}\left(\beta J\sum_{\alpha<\beta}\eta^{\alpha\beta}S^\alpha S^\beta + \sqrt{\beta J_0}\sum_\alpha\epsilon^\alpha S^\alpha\right)+\frac12\text{Tr}'e^{L_0}\left\{\left(\beta J\sum_{\alpha<\beta}\eta^{\alpha\beta}S^\alpha S^\beta + \sqrt{\beta J_0}\sum_\alpha\epsilon^\alpha S^\alpha\right)^2\right\}\right] \end{align*} 여기서 $\langle A\rangle_{L_0}=\text{Tr}'(e^{L_0}A)/\text{Tr}'e^{L_0}$로 쓰면 위 식은 \begin{align*} =&\ln\text{Tr}'e^{L_0}+\ln\left[1+\left\langle\beta J\sum_{\alpha<\beta}\eta^{\alpha\beta}S^\alpha S^\beta + \sqrt{\beta J_0}\sum_\alpha\epsilon^\alpha S^\alpha\right\rangle_{L_0}+\frac12\left\langle\left(\beta J\sum_{\alpha<\beta}\eta^{\alpha\beta}S^\alpha S^\beta + \sqrt{\beta J_0}\sum_\alpha\epsilon^\alpha S^\alpha\right)^2\right\rangle_{L_0}\right] \end{align*} 로 쓸 수 있고 $\ln(1+\langle x\rangle + \frac12\langle x\rangle^2+\cdots) = \langle x\rangle+\frac12(\langle x^2\rangle-\langle x\rangle^2)+\cdots$임과 $\epsilon^\alpha$ 및 $\eta^{\alpha\beta}$에 대한 1차항들은 극값 조건에 의해 사라진다는 조건을 적용하면 최종적으로 \begin{align*} &\ln\text{Tr}' \exp\left(L_0+\beta J\sum_{\alpha<\beta}\eta^{\alpha\beta}S^\alpha S^\beta + \sqrt{\beta J_0}\sum_\alpha\epsilon^\alpha S^\alpha\right)\\ =& \ln\text{Tr}'e^{L_0} + \frac12\beta^2J^2\sum_{\alpha<\beta}\sum_{\gamma<\delta}\eta^{\alpha\beta}\eta^{\gamma\delta}\left(\left\langle S^\alpha S^\beta S^\gamma S^\delta\right\rangle_{L_0}-\left\langle S^\alpha S^\beta \right\rangle_{L_0}\left\langle S^\gamma S^\delta \right\rangle_{L_0}\right)\\ &+ \beta J\sqrt{\beta J_0}\sum_{\alpha<\beta}\sum_\gamma\eta^{\alpha\beta}\epsilon^\gamma\left(\left\langle S^\alpha S^\beta S^\gamma\right\rangle_{L_0}-\left\langle S^\alpha S^\beta\right\rangle_{L_0}\left\langle S^\gamma\right\rangle_{L_0}\right) + \frac12 \beta J_0\sum_{\alpha\beta}\epsilon^\alpha\epsilon^\beta\left(\left\langle S^\alpha S^\beta\right\rangle_{L_0}-\left\langle S^\alpha\right\rangle_{L_0}\left\langle S^\beta\right\rangle_{L_0}\right) \end{align*} 가 된다. $\epsilon^\alpha$ 및 $\eta^{\alpha\beta}$의 2차항에 해당하는 성분을 모아 $\Delta$라고 쓰면 자유에너지를 $$\left[f\right] = -\frac{\beta J^2}{4} - \lim_{n\rightarrow0}\frac1{\beta n}\left\{-\frac14n(n-1)y^2-\frac12nx^2-\Delta\right\}$$ 의 꼴로 쓸 수 있고, \begin{align*} \Delta=&\frac12\sum_{\alpha<\beta}\sum_{\gamma<\delta}\eta^{\alpha\beta}\eta^{\gamma\delta}\left[\delta_{(\alpha\beta)(\gamma\delta)}-\beta^2J^2\left(\left\langle S^\alpha S^\beta S^\gamma S^\delta\right\rangle_{L_0}-\left\langle S^\alpha S^\beta \right\rangle_{L_0}\left\langle S^\gamma S^\delta \right\rangle_{L_0}\right)\right]\\ &+ \beta J\sqrt{\beta J_0}\sum_{\alpha<\beta}\sum_\gamma\eta^{\alpha\beta}\epsilon^\gamma\left(\left\langle S^\alpha S^\beta\right\rangle_{L_0}\left\langle S^\gamma\right\rangle_{L_0}-\left\langle S^\alpha S^\beta S^\gamma\right\rangle_{L_0}\right) + \frac12 \sum_{\alpha\beta}\epsilon^\alpha\epsilon^\beta\left[\delta_{\alpha\beta}-\beta J_0\left(\left\langle S^\alpha S^\beta\right\rangle_{L_0}-\left\langle S^\alpha\right\rangle_{L_0}\left\langle S^\beta\right\rangle_{L_0}\right)\right] \end{align*} 이다. 오해의 여지가 없으므로 앞으로 $\langle \cdots\rangle_{L_0}$을 $\langle\cdots\rangle$로 쓰자. 이제 안정성을 논할 차례인데 $\Delta$는 $\epsilon^\alpha$ 및 $\eta^{\alpha\beta}$에 대한 2차항 뿐 아니라 교차항도 포함하고 있으므로 벡터 $$ \vec\mu=\begin{pmatrix} \{\epsilon^\alpha\}\\ \{\eta^{\alpha\beta}\} \end{pmatrix} $$ 를 도입해 다음과 같은 2차 형식으로 쓸 수 있고, $$\Delta=\vec\mu^TG\vec\mu$$ 해의 안정성은 이 행렬 $G$의 고윳값의 부호를 통해 살펴볼 수 있다. 만약 모든 고윳값이 양수이면, 복제 대칭해가 극솟값이므로 복제 대칭해는 안정적일 것이다. 행렬 $G$의 각 성분은 $\epsilon^\alpha$, $\eta^{\alpha\beta}$의 계수로부터 알아낼 수 있는데 예를 들어 $\epsilon^\alpha\epsilon^\beta$항으로부터 \begin{align*} G_{\alpha\alpha} &= 1-\beta J_0(1-\langle S^\alpha\rangle^2)\\ G_{\alpha\beta} &= -\beta J_0(\langle S^\alpha S^\beta\rangle-\langle S^\alpha\rangle\langle S^\beta\rangle) \end{align*} 임을 알 수 있다. 마찬가지로 가능한 2차항의 조합을 모두 생각한다면 행렬 $G$의 성분을 다음과 같이 모두 표현할 수 있다. \begin{align*} G_{(\alpha\beta)(\alpha\beta)}&= 1-\beta^2J^2(1-\langle S^\alpha S^\beta\rangle^2)\\ G_{(\alpha\beta)(\alpha\gamma)}&= -\beta^2J^2(\langle S^\beta S^\gamma\rangle - \langle S^\alpha S^\beta\rangle\langle S^\alpha S^\gamma\rangle)\\ G_{(\alpha\beta)(\gamma\delta)}&= -\beta^2J^2(\langle S^\alpha S^\beta S^\gamma S^\delta\rangle-\langle S^\alpha S^\beta\rangle\langle S^\gamma S^\delta\rangle)\\ G_{\alpha(\alpha\beta)} &= \beta J\sqrt{\beta J_0}(\langle S^\alpha\rangle\langle S^\alpha S^\beta\rangle-\langle S^\beta\rangle)\\ G_{\gamma(\alpha\beta)} &= \beta J\sqrt{\beta J_0}(\langle S^\gamma\rangle\langle S^\alpha S^\beta\rangle-\langle S^\alpha S^\beta S^\gamma\rangle) \end{align*} \begin{align*} G_{(\alpha\beta)(\alpha\beta)}&= 1-\beta^2J^2(1-\langle S^\alpha S^\beta\rangle^2)\\ G_{(\alpha\beta)(\alpha\gamma)}&= -\beta^2J^2(\langle S^\beta S^\gamma\rangle - \langle S^\alpha S^\beta\rangle\langle S^\alpha S^\gamma\rangle)\\ G_{(\alpha\beta)(\gamma\delta)}&= -\beta^2J^2(\langle S^\alpha S^\beta S^\gamma S^\delta\rangle-\langle S^\alpha S^\beta\rangle\langle S^\gamma S^\delta\rangle)\\ G_{\alpha(\alpha\beta)} &= \beta J\sqrt{\beta J_0}(\langle S^\alpha\rangle\langle S^\alpha S^\beta\rangle-\langle S^\beta\rangle)\\ G_{\gamma(\alpha\beta)} &= \beta J\sqrt{\beta J_0}(\langle S^\gamma\rangle\langle S^\alpha S^\beta\rangle-\langle S^\alpha S^\beta S^\gamma\rangle) \end{align*} 그리고 복제 대칭성을 가정하고 있으므로 \begin{align*} \langle S^\alpha\rangle&\equiv m=\int Dz \tanh\beta\tilde H(z)\\ \langle S^\alpha S^\beta\rangle&\equiv q=\int Dz \tanh^2\beta\tilde H(z)\\ \langle S^\alpha S^\beta S^\gamma\rangle&\equiv t=\int Dz \tanh^3\beta\tilde H(z)\\ \langle S^\alpha S^\beta S^\gamma S^\delta\rangle&\equiv r=\int Dz \tanh^4\beta\tilde H(z) \end{align*} 로 쓰면 각 성분은 \begin{align*} G_{\alpha\alpha} &\equiv A = 1-\beta J_0(1-m^2)\\ G_{\alpha\beta} &\equiv B=-\beta J_0(q-m^2)\\ G_{(\alpha\beta)(\alpha\beta)}&\equiv P=1-\beta^2J^2(1-q^2)\\ G_{(\alpha\beta)(\alpha\gamma)}&\equiv Q=-\beta^2J^2(q-q^2)\\ G_{(\alpha\beta)(\gamma\delta)}&\equiv R=-\beta^2J^2(r-q^2)\\ G_{\alpha(\alpha\beta)} &\equiv C=\beta J\sqrt{\beta J_0}(mq-m)\\ G_{\gamma(\alpha\beta)} &\equiv D=\beta J\sqrt{\beta J_0}(mq-t) \end{align*} 로 간단하게 쓸 수 있다.

상자성 해의 경우 $m=q=t=r=0$이므로 대부분의 성분은 사라지고 대각 성분인 \begin{align*} A&=1-\beta J_0\\ P&=1-\beta^2 J^2 \end{align*} 만이 살아남는다. 복제 대칭해가 안정적이려면 $1-\beta J_0>0$, $1-\beta^2 J^2$를 만족해야 하는데 이 조건은 $T>J_0$, $T>J$와 같다. 위상도표에서도 알 수 있듯이 안정성을 나누는 경계가 상의 경계이므로 상자성 해의 경우엔 복제 대칭해가 항상 안정적이다.

강자성 해의 경우, $m,q\neq0$이므로 다음과 같은 고윳값방정식을 풀어야 한다. $$G\vec\mu = \lambda\vec\mu,\quad \vec\mu = \begin{pmatrix} \{\epsilon^\alpha\}\\ \{\eta^{\alpha\beta}\} \end{pmatrix}$$ 강자성 해가 안정적이려면 이 고윳값 방정식을 통해 얻어낸 $\lambda$가 모두 양수여야 할 것이다.

(1)$\epsilon^\alpha=a$, $\eta^{\alpha\beta}=b$인 경우.
이 경우는 $\vec\mu_1 = (a,\dots,a,b,\dots,b)$의 꼴로 쓰여지기 때문에 첫 번째 행과 $n+1$번째 행만 살펴보면 된다. $G$의 첫 번째 행은 $$(A,B,\dots,B,C,\dots,C,D,\dots,D)$$ 이고, 이를 $\vec\mu_1$와 곱하면 $$Aa+(n-1)Ba+(n-1)Cb+\frac12(n-1)(n-2)Db=\lambda_1a$$ 가 된다. 마찬가지로 $G$의 $n+1$번째 행은 $$(C,C,D,\dots,D,P,Q,\dots,Q,R,\dots,R)$$ 이고, $\vec\mu_1$와 곱하면 $$2Ca+(n-2)Da+Pb+2(n-2)Qb+\frac12(n-2)(n-3)Rb=\lambda_1b$$ 가 된다. 위 두 식을 연립해서 $\lambda_1$을 구하고 $n\rightarrow0$인 극한을 취해주면 $$\lambda_1 = \frac12\left(A-B+P-4Q+3R\pm\sqrt{(A-B-P+4Q-3R)^2-8(C-D)^2}\right)$$ 를 얻는다.

(2)특정 복제본 $\theta$에 대해서는 $\epsilon^\theta=a$, $\eta^{\theta\theta}=\eta^{\alpha\theta}=\eta^{\theta\alpha}= c$이고, 나머지는 $\epsilon^\alpha=b$, $\eta^{\alpha\beta}=d$인 경우.
편의상 $\theta=1$로 두자. 위의 경우와 마찬가지로 첫 번째 행과 $n+1$번째 행을 통해 \begin{align*} Aa+(n-1)Bb+Cc(n-1)+\frac12Dd(n-1)(n-2)&=\lambda_2a\\ aC+bC+(n-2)Db+Pc+(n-2)Qc+(n-2)Qd+\frac12(n-2)(n-3)Rd&=\lambda_2c \end{align*} 임을 알 수 있다. 그리고 고유벡터 $\vec\mu_2$의 $\vec\epsilon_2, \vec\eta_2$는 앞에서 구했던 $\vec\epsilon_1, \vec\eta_1$들과 각각 직교할 것이므로 $\vec\epsilon_1\cdot\vec\epsilon_2=0$, $\vec\eta_1\cdot\vec\eta_2=0$인 조건을 통해 $$a+(n-1)b=0,\quad c+\frac12(n-2)d=0$$ 를 만족해야 하므로 이를 대입하고 위 연립방정식을 푼 뒤에 $n\rightarrow0$인 극한을 취해주면 $$\lambda_2 = \frac12\left(A-B+P-4Q+3R\pm\sqrt{(A-B-P+4Q-3R)^2-8(C-D)^2}\right)$$ 를 얻는다.

(3) 특정 복제본 $\theta,\nu$에 대해 $\epsilon^\theta=\epsilon^\nu=a$이고 $\eta^{\theta\nu}=c$, $\eta^{\theta\alpha}=\eta^{\nu\alpha}=d$, 그리고 $\eta^{\alpha\beta}=3$인 경우.
이번에도 편의상 $\theta=1$, $\nu=2$로 두자. 먼저 $\vec\mu_1=(x,\dots,x,y,\dots,y)^T$와 $\vec\mu_3$의 직교조건을 이용하면 $$2a+(n-2)b=0,\quad c+2(n-2)d+\frac12(n-2)(n-3)e=0$$ 이고, $\vec\mu_2=(x,y,\dots,y,v,\dots,v,w,\dots,w)^T$와 $\vec\mu_3$의 직교조건을 이용하면 $$ax+ay+(n-2)by=0,\quad cv+(n-2)dv=0,\quad (n-2)dw+\frac12(n-2)(n-3)ew=0$$ 를 얻는데, $\vec\mu_2$의 제약조건 $x+(n-1)y=0$를 적용하면 $$a=b=0,\quad c=(2-n)d,\quad d+\frac12(n-3)e=0$$ 가 되어야 함을 알 수 있다. 따라서 $\vec\mu_3=(0,\dots,0,c,d,\dots,d,e,\dots,e)^T$를 가정하고 고윳값 방정식을 풀면 $$Pc+2(n-2)Qd+\frac12(n-2)(n-3)Re=\lambda_3c$$ 가 되고, $n\rightarrow0$인 극한을 취해주면 $$\lambda_3=P-2Q+R$$ 이 됨을 알 수 있다. 여기서 특정한 복제본 $\theta,\nu$를 선택하는 경우의 수는 $n(n-1)/2$이므로 $\lambda_3$까지만 고려하면 $G$의 차원을 모두 채우게 된다.

이제 구해낸 두 타입의 고윳값 $\lambda_1=\lambda_2$, $\lambda_3$의 부호를 살펴볼 차례이다. 먼저 $\lambda_{1,2}$가 양수일 충분조건은 $$ A-B = \frac1{J_0}\left.\frac{\partial^2[f]}{\partial m^2}\right\vert_{RS}>0,\quad P-4Q+3R=-\left.\frac2{\beta J^2}\frac{\partial^2[f]}{\partial q^2}\right\vert_{RS}>0 $$ 인데, 이는 복제 대칭해의 자유에너지를 통해 항상 성립함을 볼 수 있다. 반면, $\lambda_3>0$일 충분조건은 $$\left(\frac TJ\right)^2>\int Dz\,\text{sech}^4\left(\beta J\sqrt qz+\beta J_0m\right)$$ 인데 이 조건은 항상 성립하지는 않는다. 예를 들어, $J_0=0$이고 외부 자기장 $h$가 존재할 때 위 식을 수치적으로 풀어보면 복제 대칭해가 안정적인 영역과 그렇지 않은 영역을 구해낼 수 있다.

복제 대칭해의 스핀유리 질서맺음변수 $q_{\alpha\beta}$는 다음과 같은 행렬 형태로 쓸 수 있다. $$\left\{ q_{\alpha\beta} \right\} = \begin{pmatrix} 0& & & & & \\ &0& & &q& \\ & &0& & & \\ & & &0& & \\ &q& & &0& \\ & & & & &0\\ \end{pmatrix}$$ 그러나 드알메이다-사울리스 선 아래 영역에서는 복제 대칭해가 안정적이지 않으므로 복제 대칭해를 가정할 수 없으므로 조금 더 일반적인 해를 찾아야 한다. 여기서는 Parisi가 도입한 복제 대칭성 깨짐을 이용해 볼 것이다. 먼저 전체 $n$개의 복제본을 $m_1$개씩 묶어 총 $n/m_1$개의 블록으로 나눌 수 있다고 가정해보자. 이 때 서로 같은 블록에 있는 복제본들 사이의 스핀유리 질서맺음변서는 $q_1$, 서로 다른 블록에 있는 복제본들 사이의 스핀유리 질서맺음변서는 $q_0$이다. 예를 들어, $n=6$, $m_1=3$인 경우에 $q$는 다음과 같이 쓸 수 있다. $$\left\{ q_{\alpha\beta} \right\} = \begin{pmatrix} 0&q_1&q_1& & & \\ q_1&0&q_1& &q_0& \\ q_1&q_1&0& & & \\ & & &0&q_1&q_1\\ &q_0& &q_1&0&q_1\\ & & &q_1&q_1&0\\ \end{pmatrix}$$ 이제 이를 이용해서 1차 복제 대칭성 깨짐해의 안정성을 논해볼 것이다. 복제 대칭해와 마찬가지로 자유에너지는 $$-\beta [f] = \lim_{n\to 0} \left( -\frac{\beta^2 J^2}{4n} \sum_{\alpha \neq \beta} q_{\alpha \beta}^2 - \frac{\beta J_0}{2n} \sum_\alpha m_\alpha^2 + \frac{1}{4} \beta^2 J^2 + \frac{1}{n} \ln \text{Tr}^\prime e^L \right)$$ 로 주어지고, $$L = \beta^2 J^2 \sum_{\alpha < \beta} q_{\alpha \beta} S^\alpha S^\beta + \beta \sum_\alpha (J_0 m_\alpha + h) S^\alpha$$ 이다. $L$의 첫 번째 항은 $$\sum_{\alpha<\beta} q_{\alpha \beta} S^\alpha S^\beta = \frac12 \sum_{\alpha\neq\beta}q_{\alpha\beta}S^\alpha S^\beta= \frac{1}{2} \left[ q_0 \left( \sum_\alpha^n S^\alpha \right)^2 + (q_1-q_0) \sum_{\text{block}}^{n/m_1} \left( \sum_{\alpha \in \text{block}} S^\alpha \right)^2 - nq_1 \right]$$ 로 쓸 수 있다. 이 항은 단지 $q$의 모든 성분을 $q_0$으로 채운 뒤, 같은 블록 사이의 $q_{\alpha\beta}$를 $q_1$로 바꾸어주고 대각성분을 0으로 만든 것이다. 비슷한 방법을 사용하면 $$\lim_{n\to 0} \frac{1}{n} \sum_{\alpha \neq \beta} q_{\alpha \beta}^2 = \lim_{n \to 0} \frac{1}{n} \left[ n^2 q_0^2 + \frac{n}{m} m_1^2 (q_1^2-q_0^2) - nq_1^2 \right] = (m_1-1)q_1^2 - m_1 q_0^2$$ 가 된다. 즉, 자유에너지는 $$ -\beta[f] = -\frac{\beta^2 J^2}{4} \left[ (m_1-1)q_1^2 - m_1 q_0^2 \right] - \lim_{n\to 0} \frac{\beta J}{2n} \sum_\alpha m_\alpha^2 + \frac{1}{4} \beta^2 J^2 + \lim_{n\to 0} \frac{1}{n} \ln \text{Tr}^\prime \exp\left\{ \frac{\beta^2 J^2}{2} \left[ q_0 \left( \sum_\alpha S^\alpha \right)^2 + (q_1-q_0) \sum_{\text{block}}^{n/m_1} \left( \sum_{\alpha \in \text{block}} S^\alpha \right)^2 - nq_1 \right] + \beta \sum_\alpha (J_0 m_\alpha + h) S^\alpha \right\}$$ 이고, 하나의 $u$와 $n/m_1$개의 $v_b$에 대한 허바드-스트라토노비치 변환은 \begin{eqnarray} \exp \left[ \frac{\beta^2 J^2}{2} q_0 \left( \sum_{\alpha}^m S^\alpha \right)^2 \right] &=& \sqrt{\frac{\beta^2 J^2 q_0}{2\pi}} \int_{-\infty}^\infty du \exp\left[-\beta^2 J^2 q_0 u^2/2 + \beta^2 J^2 q_0 u \sum_\alpha^n S^\alpha \right]\\ &=& \frac{1}{2\pi} \int d\tilde{u} \exp \left( -\frac{\tilde{u}^2}{2} \right) \exp \left( \beta J \sqrt{q_0} \tilde{u} \sum_\alpha^n S^\alpha \right)\\ &=& \int D\tilde{u} \exp \left( \beta J \sqrt{q_0} \tilde{u} \sum_{\text{block}}^{n/m_1} \sum_{\text{block}}^{m_1} S^\alpha \right) \end{eqnarray} \begin{eqnarray} \exp \left[ \frac{\beta^2 J^2}{2} (q_1 - q_0) \left( \sum_{\alpha \in \text{block}}^{m_1} S^\alpha \right)^2 \right] &=& \sqrt{\frac{\beta^2 J^2 (q_1-q_0)}{2\pi}} \int_{-\infty}^\infty dv_b \exp\left[-\beta^2 J^2 (q_1-q_0) v_b^2/2 + \beta^2 J^2 (q_1-q_0) v_b \sum_\alpha^{m_1} S^\alpha \right]\\ &=& \frac{1}{2\pi} \int d\tilde{v}_b \exp \left( -\frac{\tilde{v}_b^2}{2} \right) \exp \left( \beta J \sqrt{q_1-q_0} \tilde{v}_b \sum_\alpha^{m_1} S^\alpha \right)\\ &=& \int D\tilde{v}_b \exp \left( \beta J \sqrt{q_1-q_0} \tilde{v}_b \sum_{\alpha}^{m_1} S^\alpha \right) \end{eqnarray} 가 되므로, 자유에너지의 마지막 항은 \begin{eqnarray} &&\lim_{n\to 0} \frac{1}{n} \ln \text{Tr}^\prime \exp \left\{ \frac{\beta^2 J^2}{2} \left[ q_0 \left( \sum_\alpha^n S^\alpha \right)^2 + (q_1-q_0) \sum_{\text{block}}^{n/m_1} \left( \sum_{\alpha \in \text{block}}^{m_1} S^\alpha \right)^2 - nq_1 \right] + \beta \sum_\alpha^n (J_0 m_\alpha + h) S^\alpha \right\}\\ &=& \lim_{n\to 0} \frac{1}{n} \ln \text{Tr}^\prime \int D\tilde{u} \left( \prod_b^{n/m_1} D\tilde{v}_b \right) \exp \left\{ \sum_{\text{block}}^{n/m_1}\left[ \beta J \sqrt{q_0} \tilde{u} + \beta J \sqrt{q_1-q_0} \tilde{v}_b + \beta(J_0 m +h) \right] \sum_{\alpha \in \text{block}}^{m_1} S^\alpha \right\} \exp\left(-\frac{1}{2} \beta^2 J^2 nq_1\right)\\ &=&-\frac12 \beta^2 J^2 q_1+\lim_{n\rightarrow 0}\frac1n\ln Tr'\int D\tilde u\left[\int D\tilde v\exp\left\{\left(\beta J\sqrt{q_0}\tilde u + \beta J\sqrt{q_1-q_0}\tilde v + \beta(J_0m+h)\right)\sum_{\alpha\in block}^{m_1}S^\alpha\right\}\right]^{n/m_1} \end{eqnarray} 가 된다. $\Xi = \beta J\sqrt{q_0}\tilde u + \beta J\sqrt{q_1-q_0}\tilde v + \beta(J_0m+h)$로 두고, $n\rightarrow0$인 극한을 생각하고 있으므로 $\log$와 $\exp$를 전개해서 정리하면 \begin{eqnarray*} &=&-\frac12 \beta^2J^2q_1+\lim_{n\rightarrow 0}\frac1n\log\int_{-\infty}^\infty D\tilde u\left[\int_{-\infty}^\infty D\tilde v(2\cosh\Xi)^{m_1}\right]^{n/m_1}\\ &=&-\frac12 \beta^2J^2q_1+\lim_{n\rightarrow 0}\frac1n\log\int_{-\infty}^\infty D\tilde u\exp\left[\frac{n}{m_1}\log\left\{\int_{-\infty}^\infty D\tilde v(2\cosh\Xi)^{m_1}\right\}\right]\\ &\approx&-\frac12 \beta^2J^2q_1+\lim_{n\rightarrow 0}\frac1n\log\int_{-\infty}^\infty D\tilde u\left[1+\frac{n}{m_1}\log\left\{\int_{-\infty}^\infty D\tilde v(2\cosh\Xi)^{m_1}\right\}\right]\\ &=&-\frac12 \beta^2J^2q_1+\lim_{n\rightarrow 0}\frac1n\log\left[1+\frac{n}{m_1}\int_{-\infty}^\infty D\tilde u\log\left\{\int_{-\infty}^\infty D\tilde v(2\cosh\Xi)^{m_1}\right\}\right]\\ &\approx&-\frac12 \beta^2J^2q_1+\frac{1}{m_1}\int_{-\infty}^\infty D\tilde u\log\left\{\int_{-\infty}^\infty D\tilde v(2\cosh\Xi)^{m_1}\right\}\\ &=&-\frac12 \beta^2J^2q_1+\log2+\frac{1}{m_1}\int_{-\infty}^\infty D\tilde u\log\left\{\int_{-\infty}^\infty D\tilde v\cosh^{m_1}\Xi\right\}\\ \end{eqnarray*} 과 같이 정리할 수 있으므로 최종적인 자유에너지는 $$\Rightarrow\beta f_\text{1RSB} = \frac{\beta^2J^2}{4}\{(m_1-1)q_1^2 - m_1q_0^2 + 2q_1 -1\} + \frac{\beta J_0}{2}m^2 - \log2 - \frac{1}{m_1}\int Du\log\int Dv\cosh^{m_1}\Xi$$ 임을 알 수 있다.

$m$에 대해 위 식을 최소화시키면

\begin{eqnarray} 0&=&\frac{\partial(\beta f_\text{1RSB})}{\partial m} = \beta J_0m - \frac{1}{m_1}\frac{\partial}{\partial m}\left[\int Du \log \int Dv \cosh^{m_1}\Xi\right] = \beta J_0m - \beta J_0\int Du \frac{\int Dv \cosh^{m_1-1}\Xi \sinh\Xi}{\int Dv \cosh^{m_1}\Xi}\\ \therefore m&=& \int Du \frac{\int Dv \cosh^{m_1}\Xi \tanh\Xi}{\int Dv \cosh^{m_1}\Xi}. \end{eqnarray}

$q_0$와 $q_1$에 대해 같은 방식을 적용해보면, \begin{eqnarray} 0&=&\frac{\partial(\beta f_\text{1RSB})}{\partial q_0} = -\frac{\beta^2 J^2}{2}m_1 q_0 - \frac{\beta J}{2\sqrt{q_0}} \int Du ~u\frac{\int Dv \cosh^{m_1}\Xi \tanh\Xi}{\int Dv \cosh^{m_1}\Xi} + \frac{\beta J}{2\sqrt{q_1-q_0}} \int Du \frac{\int Dv ~v\cosh^{m_1}\Xi \tanh\Xi}{\int Dv \cosh^{m_1}\Xi}, \end{eqnarray}

\begin{eqnarray} 0&=&\frac{\partial(\beta f_\text{1RSB})}{\partial q_1} = \frac{\beta^2 J^2}{4} \left[ (m_1-1) 2q_1 +2\right] - \frac{\beta J}{2\sqrt{q_1-q_0}} \int Du \frac{\int Dv ~v\cosh^{m_1}\Xi \tanh\Xi}{\int Dv \cosh^{m_1}\Xi}. \end{eqnarray}

두 식을 연립하면 다음과 같다: \begin{eqnarray} \beta J\sqrt{q_0} \int Du ~u\frac{\int Dv \cosh^{m_1}\Xi \tanh\Xi}{\int Dv \cosh^{m_1}\Xi} &=& 2q_0 \left\{ -\frac{\beta^2 J^2}{2} m_1 q_0 + \frac{\beta^2 J^2}{4} \left[ (m_1-1) 2q_1 +2 \right] \right\}\\ \beta J\sqrt{q_1-q_0} \int Du \frac{\int Dv ~v\cosh^{m_1}\Xi \tanh\Xi}{\int Dv \cosh^{m_1}\Xi} &=& 2(q_1-q_0) \frac{\beta^2 J^2}{4} \left[ (m_1-1) 2q_1 +2 \right]. \end{eqnarray}

좌변의 적분 안에 있는 $u$와 $v$를 제거하기 위해서는 부분적분을 행하면 된다. \begin{eqnarray} \beta J\sqrt{q_0} \int Du ~u\frac{\int Dv \cosh^{m_1}\Xi \tanh\Xi}{\int Dv \cosh^{m_1}\Xi} &=& \beta J\sqrt{q_0} \frac{1}{\sqrt{2\pi}} \int du ~u \exp\left( -\frac{u^2}{2} \right) \frac{\int Dv \cosh^{m_1}\Xi \tanh\Xi}{\int Dv \cosh^{m_1}\Xi}\\ &=& \beta J\sqrt{q_0} \frac{1}{\sqrt{2\pi}} \int du \frac{d}{du} \left[ - \exp\left( -\frac{u^2}{2} \right) \right] \frac{\int Dv \cosh^{m_1}\Xi \tanh\Xi}{\int Dv \cosh^{m_1}\Xi}\\ &=& \beta J\sqrt{q_0} \frac{1}{\sqrt{2\pi}} \int du \exp\left( -\frac{u^2}{2} \right) \frac{d}{du} \left( \frac{\int Dv \cosh^{m_1}\Xi \tanh\Xi}{\int Dv \cosh^{m_1}\Xi} \right)\\ &=& \beta J\sqrt{q_0} \int Du \frac{d}{du} \left( \frac{\int Dv \cosh^{m_1}\Xi \tanh\Xi}{\int Dv \cosh^{m_1}\Xi} \right)\\ &=& \beta^2 J^2 q_0 \left[ (m_1-1)\int Du \frac{ \int Dv \cosh^{m_1}\Xi \tanh^2\Xi}{\int Dv \cosh^{m_1}\Xi} + 1\right] -\beta^2 J^2 q_0 m_1 \int Du \left( \frac{ \int Dv \cosh^{m_1}\Xi \tanh\Xi}{\int Dv \cosh^{m_1}\Xi} \right)^2, \end{eqnarray}

\begin{eqnarray} \beta J\sqrt{q_1-q_0} \int Du \frac{\int Dv ~v\cosh^{m_1}\Xi \tanh\Xi}{\int Dv \cosh^{m_1}\Xi} &=& \beta^2 J^2 (q_1-q_0) \left[ (m_1-1) \int Du \frac{\int Dv \cosh^{m_1}\Xi \tanh^2\Xi}{\int Dv \cosh^{m_1}\Xi} +1 \right]. \end{eqnarray}

이제 식을 풀어보면 아래의 결과를 얻는다: \begin{eqnarray} q_0 &=& \int Du \left( \frac{ \int Dv \cosh^{m_1}\Xi \tanh\Xi}{\int Dv \cosh^{m_1}\Xi} \right)^2\\ q_1 &=&\int Du \frac{\int Dv \cosh^{m_1}\Xi \tanh^2\Xi}{\int Dv \cosh^{m_1}\Xi}. \end{eqnarray}

코시-슈바르츠 부등식에 의해 $q_1 \ge q_0$이다. $m_1$에 대해서도 최소화가 되어야 하지만 이 계산은 뒤에 쓰이지 않으므로 생략한다.

$J_0=h=0$일 때 $\Xi$는 $u$, $v$에 대해 홀함수이므로, 위 적분 표현식으로부터 $m=0$임을 알 수 있다. $q_1$에 대한 바로 앞의 식에서 $q_0$와 $q_1$이 작다고 놓고 우변을 전개하면 첫 항이 $\beta^2 J^2 q_1$이므로 $q_1$은 $T<T_f=J$에서 양수가 된다. 이는 복제대칭해에서 본 것과 동일한 결과이다.

• 평균장 이론
• 무작위장 이징 모형

• H. Nishimori, Statistical physics of spin glasses and information processing an introduction (Clarendon, Oxford, 2001).
• Scott Kirkpatrick and David Sherrington, Infinite-ranged models of spin-glasses, Phys. Rev. B 17, 4384 (1978).